python assignment in loop

How to use Python While with Assignment[4 Examples]

In this Python tutorial, you will learn “ How to use Python While with Assignment “, with multiple examples and different approaches.

While working on a project, I was assigned to optimise the code. In the research, I found that we can assign variables within a while loop in Python. This helps to reduce some lines of code.

Generally, we use the ” = “ assignment operator to assign the variable in Python. But we will also try the walrus operator “:= “ to assign the variable within the while loop in Python.

Let’s understand every example one by one with some practical scenarios.

Table of Contents

Python while loop with the assignment using the “=” operator

First, we will use the “=” operator, an assignment operator in Python. This operator is used to assign a value to a variable, and we will assign a variable inside the loop in Python using the ” = “ operator.

Let’s see how Python, while with assignment, works.

In the above code, we always initialize the while loop with the true condition. “ while True :” means it will iterate infinite times and then assign the variable ‘line = “Hello” inside the while loop with one default string value.

Then assigned i = 0 , and again initialize nested while loop “print(line[i],’-‘,ord(line[i])) ” to target every character one by one and print its ascii value using ord() method in Python

Python assign variables in the while condition using the walrus operator

We can also use the walrus operator ” := “, a new assignment expression operator introduced in the 3.8 version of Python. It can create a new variable inside the expression even if that variable does not exist previously.

Let’s see how we can use it in a while loop:

Python assign variable in while condition using walrus operator

In the above code, we have a list named capitals. Then we initialize a while loop and create current_capital , giving a value as capitals.pop(0) , which means removing the first element in every iteration using the walrus operator like this: ‘current_capital:= capitals.pop(0)) != “Austin” .

When it iterates at “Austin”, the condition will be False because “Austin” != “Austin” will return false, and the loop will stop iterating.

Python while with assignment by taking user input

Here, we will see how Python While with Assignment will work if we take user input with a while loop using the walrus operator in Python.

python while assignment with walrus operator in python

In the above code, we are initializing a variable with a while loop and taking user input for an integer. Then, it will check whether the number is even or odd using the % operator.

Look at how it asks the user to enter the number repeatedly because we are not giving a break statement anywhere so it will work infinite times.

Python While with Assignment by calling the function

Now, we will see how to assign a variable inside a while loop in Python by calling the function name. We will create a user-defined function so you will understand how it is working.

How Python While with Assignment can be created by calling the user-defined function.

Python While with Assignment by calling the function

In the above code, we create a function called get_ascii_value() . This function takes a string as a parameter and returns the ASCII value of each character.

Then, we initialize a while loop, taking user_input as a string. The result variable calls a function and returns a character and ASCII value in a dictionary datatype.

In this Python article, you learned how to use Python while with assignment with different approaches and examples. We tried to cover all types of scenarios, such as creating user-defined functions , assigning within a while loop, taking user input, etc.

Python Enhancement Proposals

Python »
PEP Index »

PEP 572 – Assignment Expressions

The importance of real code, exceptional cases, scope of the target, relative precedence of :=, change to evaluation order, differences between assignment expressions and assignment statements, specification changes during implementation, _pydecimal.py, datetime.py, sysconfig.py, simplifying list comprehensions, capturing condition values, changing the scope rules for comprehensions, alternative spellings, special-casing conditional statements, special-casing comprehensions, lowering operator precedence, allowing commas to the right, always requiring parentheses, why not just turn existing assignment into an expression, with assignment expressions, why bother with assignment statements, why not use a sublocal scope and prevent namespace pollution, style guide recommendations, acknowledgements, a numeric example, appendix b: rough code translations for comprehensions, appendix c: no changes to scope semantics.

This is a proposal for creating a way to assign to variables within an expression using the notation NAME := expr .

As part of this change, there is also an update to dictionary comprehension evaluation order to ensure key expressions are executed before value expressions (allowing the key to be bound to a name and then re-used as part of calculating the corresponding value).

During discussion of this PEP, the operator became informally known as “the walrus operator”. The construct’s formal name is “Assignment Expressions” (as per the PEP title), but they may also be referred to as “Named Expressions” (e.g. the CPython reference implementation uses that name internally).

Naming the result of an expression is an important part of programming, allowing a descriptive name to be used in place of a longer expression, and permitting reuse. Currently, this feature is available only in statement form, making it unavailable in list comprehensions and other expression contexts.

Additionally, naming sub-parts of a large expression can assist an interactive debugger, providing useful display hooks and partial results. Without a way to capture sub-expressions inline, this would require refactoring of the original code; with assignment expressions, this merely requires the insertion of a few name := markers. Removing the need to refactor reduces the likelihood that the code be inadvertently changed as part of debugging (a common cause of Heisenbugs), and is easier to dictate to another programmer.

During the development of this PEP many people (supporters and critics both) have had a tendency to focus on toy examples on the one hand, and on overly complex examples on the other.

The danger of toy examples is twofold: they are often too abstract to make anyone go “ooh, that’s compelling”, and they are easily refuted with “I would never write it that way anyway”.

The danger of overly complex examples is that they provide a convenient strawman for critics of the proposal to shoot down (“that’s obfuscated”).

Yet there is some use for both extremely simple and extremely complex examples: they are helpful to clarify the intended semantics. Therefore, there will be some of each below.

However, in order to be compelling , examples should be rooted in real code, i.e. code that was written without any thought of this PEP, as part of a useful application, however large or small. Tim Peters has been extremely helpful by going over his own personal code repository and picking examples of code he had written that (in his view) would have been clearer if rewritten with (sparing) use of assignment expressions. His conclusion: the current proposal would have allowed a modest but clear improvement in quite a few bits of code.

Another use of real code is to observe indirectly how much value programmers place on compactness. Guido van Rossum searched through a Dropbox code base and discovered some evidence that programmers value writing fewer lines over shorter lines.

Case in point: Guido found several examples where a programmer repeated a subexpression, slowing down the program, in order to save one line of code, e.g. instead of writing:

they would write:

Another example illustrates that programmers sometimes do more work to save an extra level of indentation:

This code tries to match pattern2 even if pattern1 has a match (in which case the match on pattern2 is never used). The more efficient rewrite would have been:

Syntax and semantics

In most contexts where arbitrary Python expressions can be used, a named expression can appear. This is of the form NAME := expr where expr is any valid Python expression other than an unparenthesized tuple, and NAME is an identifier.

The value of such a named expression is the same as the incorporated expression, with the additional side-effect that the target is assigned that value:

There are a few places where assignment expressions are not allowed, in order to avoid ambiguities or user confusion:

This rule is included to simplify the choice for the user between an assignment statement and an assignment expression – there is no syntactic position where both are valid.

Again, this rule is included to avoid two visually similar ways of saying the same thing.

This rule is included to disallow excessively confusing code, and because parsing keyword arguments is complex enough already.

This rule is included to discourage side effects in a position whose exact semantics are already confusing to many users (cf. the common style recommendation against mutable default values), and also to echo the similar prohibition in calls (the previous bullet).

The reasoning here is similar to the two previous cases; this ungrouped assortment of symbols and operators composed of : and = is hard to read correctly.

This allows lambda to always bind less tightly than := ; having a name binding at the top level inside a lambda function is unlikely to be of value, as there is no way to make use of it. In cases where the name will be used more than once, the expression is likely to need parenthesizing anyway, so this prohibition will rarely affect code.

This shows that what looks like an assignment operator in an f-string is not always an assignment operator. The f-string parser uses : to indicate formatting options. To preserve backwards compatibility, assignment operator usage inside of f-strings must be parenthesized. As noted above, this usage of the assignment operator is not recommended.

An assignment expression does not introduce a new scope. In most cases the scope in which the target will be bound is self-explanatory: it is the current scope. If this scope contains a nonlocal or global declaration for the target, the assignment expression honors that. A lambda (being an explicit, if anonymous, function definition) counts as a scope for this purpose.

There is one special case: an assignment expression occurring in a list, set or dict comprehension or in a generator expression (below collectively referred to as “comprehensions”) binds the target in the containing scope, honoring a nonlocal or global declaration for the target in that scope, if one exists. For the purpose of this rule the containing scope of a nested comprehension is the scope that contains the outermost comprehension. A lambda counts as a containing scope.

The motivation for this special case is twofold. First, it allows us to conveniently capture a “witness” for an any() expression, or a counterexample for all() , for example:

Second, it allows a compact way of updating mutable state from a comprehension, for example:

However, an assignment expression target name cannot be the same as a for -target name appearing in any comprehension containing the assignment expression. The latter names are local to the comprehension in which they appear, so it would be contradictory for a contained use of the same name to refer to the scope containing the outermost comprehension instead.

For example, [i := i+1 for i in range(5)] is invalid: the for i part establishes that i is local to the comprehension, but the i := part insists that i is not local to the comprehension. The same reason makes these examples invalid too:

While it’s technically possible to assign consistent semantics to these cases, it’s difficult to determine whether those semantics actually make sense in the absence of real use cases. Accordingly, the reference implementation [1] will ensure that such cases raise SyntaxError , rather than executing with implementation defined behaviour.

This restriction applies even if the assignment expression is never executed:

For the comprehension body (the part before the first “for” keyword) and the filter expression (the part after “if” and before any nested “for”), this restriction applies solely to target names that are also used as iteration variables in the comprehension. Lambda expressions appearing in these positions introduce a new explicit function scope, and hence may use assignment expressions with no additional restrictions.

Due to design constraints in the reference implementation (the symbol table analyser cannot easily detect when names are re-used between the leftmost comprehension iterable expression and the rest of the comprehension), named expressions are disallowed entirely as part of comprehension iterable expressions (the part after each “in”, and before any subsequent “if” or “for” keyword):

A further exception applies when an assignment expression occurs in a comprehension whose containing scope is a class scope. If the rules above were to result in the target being assigned in that class’s scope, the assignment expression is expressly invalid. This case also raises SyntaxError :

(The reason for the latter exception is the implicit function scope created for comprehensions – there is currently no runtime mechanism for a function to refer to a variable in the containing class scope, and we do not want to add such a mechanism. If this issue ever gets resolved this special case may be removed from the specification of assignment expressions. Note that the problem already exists for using a variable defined in the class scope from a comprehension.)

See Appendix B for some examples of how the rules for targets in comprehensions translate to equivalent code.

The := operator groups more tightly than a comma in all syntactic positions where it is legal, but less tightly than all other operators, including or , and , not , and conditional expressions ( A if C else B ). As follows from section “Exceptional cases” above, it is never allowed at the same level as = . In case a different grouping is desired, parentheses should be used.

The := operator may be used directly in a positional function call argument; however it is invalid directly in a keyword argument.

Some examples to clarify what’s technically valid or invalid:

Most of the “valid” examples above are not recommended, since human readers of Python source code who are quickly glancing at some code may miss the distinction. But simple cases are not objectionable:

This PEP recommends always putting spaces around := , similar to PEP 8 ’s recommendation for = when used for assignment, whereas the latter disallows spaces around = used for keyword arguments.)

In order to have precisely defined semantics, the proposal requires evaluation order to be well-defined. This is technically not a new requirement, as function calls may already have side effects. Python already has a rule that subexpressions are generally evaluated from left to right. However, assignment expressions make these side effects more visible, and we propose a single change to the current evaluation order:

In a dict comprehension {X: Y for ...} , Y is currently evaluated before X . We propose to change this so that X is evaluated before Y . (In a dict display like {X: Y} this is already the case, and also in dict((X, Y) for ...) which should clearly be equivalent to the dict comprehension.)

Most importantly, since := is an expression, it can be used in contexts where statements are illegal, including lambda functions and comprehensions.

Conversely, assignment expressions don’t support the advanced features found in assignment statements:

Multiple targets are not directly supported: x = y = z = 0 # Equivalent: (z := (y := (x := 0)))
Single assignment targets other than a single NAME are not supported: # No equivalent a [ i ] = x self . rest = []
Priority around commas is different: x = 1 , 2 # Sets x to (1, 2) ( x := 1 , 2 ) # Sets x to 1
Iterable packing and unpacking (both regular or extended forms) are not supported: # Equivalent needs extra parentheses loc = x , y # Use (loc := (x, y)) info = name , phone , * rest # Use (info := (name, phone, *rest)) # No equivalent px , py , pz = position name , phone , email , * other_info = contact
Inline type annotations are not supported: # Closest equivalent is "p: Optional[int]" as a separate declaration p : Optional [ int ] = None
Augmented assignment is not supported: total += tax # Equivalent: (total := total + tax)

The following changes have been made based on implementation experience and additional review after the PEP was first accepted and before Python 3.8 was released:

for consistency with other similar exceptions, and to avoid locking in an exception name that is not necessarily going to improve clarity for end users, the originally proposed TargetScopeError subclass of SyntaxError was dropped in favour of just raising SyntaxError directly. [3]
due to a limitation in CPython’s symbol table analysis process, the reference implementation raises SyntaxError for all uses of named expressions inside comprehension iterable expressions, rather than only raising them when the named expression target conflicts with one of the iteration variables in the comprehension. This could be revisited given sufficiently compelling examples, but the extra complexity needed to implement the more selective restriction doesn’t seem worthwhile for purely hypothetical use cases.

Examples from the Python standard library

env_base is only used on these lines, putting its assignment on the if moves it as the “header” of the block.

Current: env_base = os . environ . get ( "PYTHONUSERBASE" , None ) if env_base : return env_base
Improved: if env_base := os . environ . get ( "PYTHONUSERBASE" , None ): return env_base

Avoid nested if and remove one indentation level.

Current: if self . _is_special : ans = self . _check_nans ( context = context ) if ans : return ans
Improved: if self . _is_special and ( ans := self . _check_nans ( context = context )): return ans

Code looks more regular and avoid multiple nested if. (See Appendix A for the origin of this example.)

Current: reductor = dispatch_table . get ( cls ) if reductor : rv = reductor ( x ) else : reductor = getattr ( x , "__reduce_ex__" , None ) if reductor : rv = reductor ( 4 ) else : reductor = getattr ( x , "__reduce__" , None ) if reductor : rv = reductor () else : raise Error ( "un(deep)copyable object of type %s " % cls )
Improved: if reductor := dispatch_table . get ( cls ): rv = reductor ( x ) elif reductor := getattr ( x , "__reduce_ex__" , None ): rv = reductor ( 4 ) elif reductor := getattr ( x , "__reduce__" , None ): rv = reductor () else : raise Error ( "un(deep)copyable object of type %s " % cls )

tz is only used for s += tz , moving its assignment inside the if helps to show its scope.

Current: s = _format_time ( self . _hour , self . _minute , self . _second , self . _microsecond , timespec ) tz = self . _tzstr () if tz : s += tz return s
Improved: s = _format_time ( self . _hour , self . _minute , self . _second , self . _microsecond , timespec ) if tz := self . _tzstr (): s += tz return s

Calling fp.readline() in the while condition and calling .match() on the if lines make the code more compact without making it harder to understand.

Current: while True : line = fp . readline () if not line : break m = define_rx . match ( line ) if m : n , v = m . group ( 1 , 2 ) try : v = int ( v ) except ValueError : pass vars [ n ] = v else : m = undef_rx . match ( line ) if m : vars [ m . group ( 1 )] = 0
Improved: while line := fp . readline (): if m := define_rx . match ( line ): n , v = m . group ( 1 , 2 ) try : v = int ( v ) except ValueError : pass vars [ n ] = v elif m := undef_rx . match ( line ): vars [ m . group ( 1 )] = 0

A list comprehension can map and filter efficiently by capturing the condition:

Similarly, a subexpression can be reused within the main expression, by giving it a name on first use:

Note that in both cases the variable y is bound in the containing scope (i.e. at the same level as results or stuff ).

Assignment expressions can be used to good effect in the header of an if or while statement:

Particularly with the while loop, this can remove the need to have an infinite loop, an assignment, and a condition. It also creates a smooth parallel between a loop which simply uses a function call as its condition, and one which uses that as its condition but also uses the actual value.

An example from the low-level UNIX world:

Rejected alternative proposals

Proposals broadly similar to this one have come up frequently on python-ideas. Below are a number of alternative syntaxes, some of them specific to comprehensions, which have been rejected in favour of the one given above.

A previous version of this PEP proposed subtle changes to the scope rules for comprehensions, to make them more usable in class scope and to unify the scope of the “outermost iterable” and the rest of the comprehension. However, this part of the proposal would have caused backwards incompatibilities, and has been withdrawn so the PEP can focus on assignment expressions.

Broadly the same semantics as the current proposal, but spelled differently.

Since EXPR as NAME already has meaning in import , except and with statements (with different semantics), this would create unnecessary confusion or require special-casing (e.g. to forbid assignment within the headers of these statements).

(Note that with EXPR as VAR does not simply assign the value of EXPR to VAR – it calls EXPR.__enter__() and assigns the result of that to VAR .)

Additional reasons to prefer := over this spelling include:

In if f(x) as y the assignment target doesn’t jump out at you – it just reads like if f x blah blah and it is too similar visually to if f(x) and y .
import foo as bar
except Exc as var
with ctxmgr() as var

To the contrary, the assignment expression does not belong to the if or while that starts the line, and we intentionally allow assignment expressions in other contexts as well.

NAME = EXPR
if NAME := EXPR

reinforces the visual recognition of assignment expressions.

This syntax is inspired by languages such as R and Haskell, and some programmable calculators. (Note that a left-facing arrow y <- f(x) is not possible in Python, as it would be interpreted as less-than and unary minus.) This syntax has a slight advantage over ‘as’ in that it does not conflict with with , except and import , but otherwise is equivalent. But it is entirely unrelated to Python’s other use of -> (function return type annotations), and compared to := (which dates back to Algol-58) it has a much weaker tradition.

This has the advantage that leaked usage can be readily detected, removing some forms of syntactic ambiguity. However, this would be the only place in Python where a variable’s scope is encoded into its name, making refactoring harder.

Execution order is inverted (the indented body is performed first, followed by the “header”). This requires a new keyword, unless an existing keyword is repurposed (most likely with: ). See PEP 3150 for prior discussion on this subject (with the proposed keyword being given: ).

This syntax has fewer conflicts than as does (conflicting only with the raise Exc from Exc notation), but is otherwise comparable to it. Instead of paralleling with expr as target: (which can be useful but can also be confusing), this has no parallels, but is evocative.

One of the most popular use-cases is if and while statements. Instead of a more general solution, this proposal enhances the syntax of these two statements to add a means of capturing the compared value:

This works beautifully if and ONLY if the desired condition is based on the truthiness of the captured value. It is thus effective for specific use-cases (regex matches, socket reads that return '' when done), and completely useless in more complicated cases (e.g. where the condition is f(x) < 0 and you want to capture the value of f(x) ). It also has no benefit to list comprehensions.

Advantages: No syntactic ambiguities. Disadvantages: Answers only a fraction of possible use-cases, even in if / while statements.

Another common use-case is comprehensions (list/set/dict, and genexps). As above, proposals have been made for comprehension-specific solutions.

This brings the subexpression to a location in between the ‘for’ loop and the expression. It introduces an additional language keyword, which creates conflicts. Of the three, where reads the most cleanly, but also has the greatest potential for conflict (e.g. SQLAlchemy and numpy have where methods, as does tkinter.dnd.Icon in the standard library).

As above, but reusing the with keyword. Doesn’t read too badly, and needs no additional language keyword. Is restricted to comprehensions, though, and cannot as easily be transformed into “longhand” for-loop syntax. Has the C problem that an equals sign in an expression can now create a name binding, rather than performing a comparison. Would raise the question of why “with NAME = EXPR:” cannot be used as a statement on its own.

As per option 2, but using as rather than an equals sign. Aligns syntactically with other uses of as for name binding, but a simple transformation to for-loop longhand would create drastically different semantics; the meaning of with inside a comprehension would be completely different from the meaning as a stand-alone statement, while retaining identical syntax.

Regardless of the spelling chosen, this introduces a stark difference between comprehensions and the equivalent unrolled long-hand form of the loop. It is no longer possible to unwrap the loop into statement form without reworking any name bindings. The only keyword that can be repurposed to this task is with , thus giving it sneakily different semantics in a comprehension than in a statement; alternatively, a new keyword is needed, with all the costs therein.

There are two logical precedences for the := operator. Either it should bind as loosely as possible, as does statement-assignment; or it should bind more tightly than comparison operators. Placing its precedence between the comparison and arithmetic operators (to be precise: just lower than bitwise OR) allows most uses inside while and if conditions to be spelled without parentheses, as it is most likely that you wish to capture the value of something, then perform a comparison on it:

Once find() returns -1, the loop terminates. If := binds as loosely as = does, this would capture the result of the comparison (generally either True or False ), which is less useful.

While this behaviour would be convenient in many situations, it is also harder to explain than “the := operator behaves just like the assignment statement”, and as such, the precedence for := has been made as close as possible to that of = (with the exception that it binds tighter than comma).

Some critics have claimed that the assignment expressions should allow unparenthesized tuples on the right, so that these two would be equivalent:

(With the current version of the proposal, the latter would be equivalent to ((point := x), y) .)

However, adopting this stance would logically lead to the conclusion that when used in a function call, assignment expressions also bind less tight than comma, so we’d have the following confusing equivalence:

The less confusing option is to make := bind more tightly than comma.

It’s been proposed to just always require parentheses around an assignment expression. This would resolve many ambiguities, and indeed parentheses will frequently be needed to extract the desired subexpression. But in the following cases the extra parentheses feel redundant:

Frequently Raised Objections

C and its derivatives define the = operator as an expression, rather than a statement as is Python’s way. This allows assignments in more contexts, including contexts where comparisons are more common. The syntactic similarity between if (x == y) and if (x = y) belies their drastically different semantics. Thus this proposal uses := to clarify the distinction.

The two forms have different flexibilities. The := operator can be used inside a larger expression; the = statement can be augmented to += and its friends, can be chained, and can assign to attributes and subscripts.

Previous revisions of this proposal involved sublocal scope (restricted to a single statement), preventing name leakage and namespace pollution. While a definite advantage in a number of situations, this increases complexity in many others, and the costs are not justified by the benefits. In the interests of language simplicity, the name bindings created here are exactly equivalent to any other name bindings, including that usage at class or module scope will create externally-visible names. This is no different from for loops or other constructs, and can be solved the same way: del the name once it is no longer needed, or prefix it with an underscore.

(The author wishes to thank Guido van Rossum and Christoph Groth for their suggestions to move the proposal in this direction. [2] )

As expression assignments can sometimes be used equivalently to statement assignments, the question of which should be preferred will arise. For the benefit of style guides such as PEP 8 , two recommendations are suggested.

If either assignment statements or assignment expressions can be used, prefer statements; they are a clear declaration of intent.
If using assignment expressions would lead to ambiguity about execution order, restructure it to use statements instead.

The authors wish to thank Alyssa Coghlan and Steven D’Aprano for their considerable contributions to this proposal, and members of the core-mentorship mailing list for assistance with implementation.

Appendix A: Tim Peters’s findings

Here’s a brief essay Tim Peters wrote on the topic.

I dislike “busy” lines of code, and also dislike putting conceptually unrelated logic on a single line. So, for example, instead of:

instead. So I suspected I’d find few places I’d want to use assignment expressions. I didn’t even consider them for lines already stretching halfway across the screen. In other cases, “unrelated” ruled:

is a vast improvement over the briefer:

The original two statements are doing entirely different conceptual things, and slamming them together is conceptually insane.

In other cases, combining related logic made it harder to understand, such as rewriting:

as the briefer:

The while test there is too subtle, crucially relying on strict left-to-right evaluation in a non-short-circuiting or method-chaining context. My brain isn’t wired that way.

But cases like that were rare. Name binding is very frequent, and “sparse is better than dense” does not mean “almost empty is better than sparse”. For example, I have many functions that return None or 0 to communicate “I have nothing useful to return in this case, but since that’s expected often I’m not going to annoy you with an exception”. This is essentially the same as regular expression search functions returning None when there is no match. So there was lots of code of the form:

I find that clearer, and certainly a bit less typing and pattern-matching reading, as:

It’s also nice to trade away a small amount of horizontal whitespace to get another _line_ of surrounding code on screen. I didn’t give much weight to this at first, but it was so very frequent it added up, and I soon enough became annoyed that I couldn’t actually run the briefer code. That surprised me!

There are other cases where assignment expressions really shine. Rather than pick another from my code, Kirill Balunov gave a lovely example from the standard library’s copy() function in copy.py :

The ever-increasing indentation is semantically misleading: the logic is conceptually flat, “the first test that succeeds wins”:

Using easy assignment expressions allows the visual structure of the code to emphasize the conceptual flatness of the logic; ever-increasing indentation obscured it.

A smaller example from my code delighted me, both allowing to put inherently related logic in a single line, and allowing to remove an annoying “artificial” indentation level:

That if is about as long as I want my lines to get, but remains easy to follow.

So, in all, in most lines binding a name, I wouldn’t use assignment expressions, but because that construct is so very frequent, that leaves many places I would. In most of the latter, I found a small win that adds up due to how often it occurs, and in the rest I found a moderate to major win. I’d certainly use it more often than ternary if , but significantly less often than augmented assignment.

I have another example that quite impressed me at the time.

Where all variables are positive integers, and a is at least as large as the n’th root of x, this algorithm returns the floor of the n’th root of x (and roughly doubling the number of accurate bits per iteration):

It’s not obvious why that works, but is no more obvious in the “loop and a half” form. It’s hard to prove correctness without building on the right insight (the “arithmetic mean - geometric mean inequality”), and knowing some non-trivial things about how nested floor functions behave. That is, the challenges are in the math, not really in the coding.

If you do know all that, then the assignment-expression form is easily read as “while the current guess is too large, get a smaller guess”, where the “too large?” test and the new guess share an expensive sub-expression.

To my eyes, the original form is harder to understand:

This appendix attempts to clarify (though not specify) the rules when a target occurs in a comprehension or in a generator expression. For a number of illustrative examples we show the original code, containing a comprehension, and the translation, where the comprehension has been replaced by an equivalent generator function plus some scaffolding.

Since [x for ...] is equivalent to list(x for ...) these examples all use list comprehensions without loss of generality. And since these examples are meant to clarify edge cases of the rules, they aren’t trying to look like real code.

Note: comprehensions are already implemented via synthesizing nested generator functions like those in this appendix. The new part is adding appropriate declarations to establish the intended scope of assignment expression targets (the same scope they resolve to as if the assignment were performed in the block containing the outermost comprehension). For type inference purposes, these illustrative expansions do not imply that assignment expression targets are always Optional (but they do indicate the target binding scope).

Let’s start with a reminder of what code is generated for a generator expression without assignment expression.

Original code (EXPR usually references VAR): def f (): a = [ EXPR for VAR in ITERABLE ]
Translation (let’s not worry about name conflicts): def f (): def genexpr ( iterator ): for VAR in iterator : yield EXPR a = list ( genexpr ( iter ( ITERABLE )))

Let’s add a simple assignment expression.

Original code: def f (): a = [ TARGET := EXPR for VAR in ITERABLE ]
Translation: def f (): if False : TARGET = None # Dead code to ensure TARGET is a local variable def genexpr ( iterator ): nonlocal TARGET for VAR in iterator : TARGET = EXPR yield TARGET a = list ( genexpr ( iter ( ITERABLE )))

Let’s add a global TARGET declaration in f() .

Original code: def f (): global TARGET a = [ TARGET := EXPR for VAR in ITERABLE ]
Translation: def f (): global TARGET def genexpr ( iterator ): global TARGET for VAR in iterator : TARGET = EXPR yield TARGET a = list ( genexpr ( iter ( ITERABLE )))

Or instead let’s add a nonlocal TARGET declaration in f() .

Original code: def g (): TARGET = ... def f (): nonlocal TARGET a = [ TARGET := EXPR for VAR in ITERABLE ]
Translation: def g (): TARGET = ... def f (): nonlocal TARGET def genexpr ( iterator ): nonlocal TARGET for VAR in iterator : TARGET = EXPR yield TARGET a = list ( genexpr ( iter ( ITERABLE )))

Finally, let’s nest two comprehensions.

Original code: def f (): a = [[ TARGET := i for i in range ( 3 )] for j in range ( 2 )] # I.e., a = [[0, 1, 2], [0, 1, 2]] print ( TARGET ) # prints 2
Translation: def f (): if False : TARGET = None def outer_genexpr ( outer_iterator ): nonlocal TARGET def inner_generator ( inner_iterator ): nonlocal TARGET for i in inner_iterator : TARGET = i yield i for j in outer_iterator : yield list ( inner_generator ( range ( 3 ))) a = list ( outer_genexpr ( range ( 2 ))) print ( TARGET )

Because it has been a point of confusion, note that nothing about Python’s scoping semantics is changed. Function-local scopes continue to be resolved at compile time, and to have indefinite temporal extent at run time (“full closures”). Example:

This document has been placed in the public domain.

Source: https://github.com/python/peps/blob/main/peps/pep-0572.rst

Last modified: 2023-10-11 12:05:51 GMT

8 Python while Loop Examples for Beginners

learn python
python basics

What is a while loop in Python? These eight Python while loop examples will show you how it works and how to use it properly.

In programming, looping refers to repeating the same operation or task multiple times. In Python, there are two different loop types, the while loop and the for loop. The main difference between them is the way they define the execution cycle or the stopping criteria.

The for loop goes through a collection of items and executes the code inside the loop for every item in the collection. There are different object types in Python that can be used as this collection, such as lists , sets , ranges, and strings .

On the other hand, the while loop takes in a condition and continues the execution as long as the condition is met. In other words, it stops the execution when the condition becomes false (i.e. is not met).

The for loop requires a collection of items to loop over. The while loop is more general and does not require a collection; we can use it by providing a condition only.

In this article, we will examine 8 examples to help you obtain a comprehensive understanding of while loops in Python.

Example 1: Basic Python While Loop

Let’s go over a simple Python while loop example to understand its structure and functionality:

The condition in this while loop example is that the variable i must be less than 5. The initial value of the variable i is set to 0 before the while loop. The while loop first checks the condition. Since 0 is less than 5, the code inside the while loop is executed: it prints the value of i and then increments i’s value by 1. Now the value of i is 1. Then the code returns to the beginning of the while loop. Since 1 is less than 5, the code inside the while loop is executed again.

This looping is repeated until the i variable becomes 5. When the i variable becomes 5, the condition i < 5 stops being true and the execution of the while loop stops. This Python while loop can be translated to plain English as “while i is less than 5, print i and increment its value by 1”.

There are several use cases for while loops. Let’s discover them by solving some Python while loop examples. Make sure to visit our Python Basics: Part 1 course to learn more about while loops and other basic concepts.

Example 2: Using a Counter in a while Loop

We don’t always know beforehand how many times the code inside a while loop will be executed. Hence, it’s a good practice to set up a counter inside the loop. In the following Python while loop example, you can see how a counter can be used:

We start by creating the counter variable by setting its value to 0. In this case, we ask the user to input a number between 0 and 10. The condition in the while loop checks if the user input is equal to 5. As long as the input is not equal to 5, the code inside the loop will be executed so the user will be prompted to enter a number.

When the user guesses the correct number (i.e. the input is equal to 5), the code exits the loop. Then we tell the user how many guesses it took to guess the correct number by printing the value of the counter. Feel free to test it yourself in your coding environment to see how the counter works in this example.

Example 3: A while Loop with a List

Although for loops are preferred when you want to loop over a list , we can also use a while loop for this task. If we do, we need to set the while loop condition carefully. The following code snippet loops over a list called cities and prints the name of each city in the list:

There are two things to understand about how this while loop works. The len() function gives us the length of the cities list, which is equal to the number of items in the list. The variable i is used in two places. The first one is in the while loop condition, where we compare it to the length of the list. The second one is in the list index to select the item to be printed from the list. The variable is initialized with the value of 0. The expression cities[0] selects the first item in the list, which is London.

After the print() function is executed inside the while loop, the value of i is incremented by 1 and cities[1] selects the second item from the list, and so on. The code exits the loop when i becomes 4. By then, all the items in the list will have been printed out.

Lists are one of the most frequently used data structures in Python. To write efficient programs, you need to have a comprehensive understanding of lists and how to interact with them. You can find beginner-level Python list exercises in this article .

Example 4: A while Loop with a Dictionary

Constructing a while loop with a dictionary is similar to constructing a while loop with a list. However, we need a couple of extra operations because a dictionary is a more complex data structure.

If you want to learn more about Python data structures, we offer the Python Data Structures in Practice course that uses interactive exercises to explain the said data structures.

A dictionary in Python consists of key-value pairs. What do we mean by key-value pairs? This describes a two-part data structure where the value is associated with the key. In the following dictionary, names are the keys and the corresponding numeric scores are the dictionary values:

There are different ways of iterating over a dictionary. We’ll create a Python while loop that goes over the scores dictionary and prints the names and their scores:

The keys() method returns the dictionary keys, which are then converted to a list using the list() constructor. Thus, the keys variable created before the while loop is ['Jane', 'John', 'Emily'] . The while loop condition is similar to the previous example. The code inside the loop is executed until the value of i becomes more than the number of items in the dictionary (i.e. the length of the dictionary). The expression keys[i] gives us the i th item in the keys list. The expression scores[keys[i]] gives us the value of the key given by keys[i] . For example, the first item in the keys list is Jane and scores['Jane'] returns the value associated with Jane in the scores dictionary, which is 88.

Example 5: Nested while Loops

A nested while loop is simply a while loop inside another while loop. We provide separate conditions for each while loop. We also need to make sure to do the increments properly so that the code does not go into an infinite loop.

In the following Python while loop example, we have a while loop nested in another while loop:

The result output has been shortened for demonstration purposes.

The first loop goes over integers from 1 to 9. For each iteration of the first while loop (i.e. for each number from 1 to 9), the while loop inside (i.e. the nested loop) is executed. The nested loop in our example also goes over integers from 1 to 9.

The execution inside the second while loop is multiplying the values of i and j . The i is the value from the outer while loop and j is the value from the nested while loop. Thus, the code iterates integers from 1 to 9 for every integer from 1 to 9.

In the result, we have a multiplication table. The important point here is to do the increments accurately. The variables i and j must each be incremented inside their own while loop.

Example 6: Infinite Loops and the break Statement

Since while loops continue execution until the given condition is no longer met, we can end up in an infinite loop if the condition is not set properly.

The following is an example of an infinite while loop. The initial value of i is 10 and the while loop checks if the value of i is greater than 5, which is true. Inside the loop, we print the value of i and increment it by 1 so it’ll always be more than 5 and the while loop will continue execution forever.

Another way to create infinite while loops is by giving the condition as while True .

The break statement provides a way to exit the loop. Even if the condition is still true, when the code sees the break , it’ll exit the loop. Let’s do a Python while loop example to show how break works:

The while loop goes over the scores list and prints the items in it. Before it prints the item, there is an if statement that checks if the item is an integer. If not, the code exits the while loop because of the break statement. If the item is an integer, the loop execution continues and the item is printed.

Example 7: Using continue in a while Loop

The continue statement is quite similar to the break statement. The break command exits the while loop so the code continues executing the next piece of code if there is any. On the other hand, continue returns the control to the beginning of the while loop so the execution of the while loop continues using the next value. Let’s repeat the previous while loop example, this time using continue instead of break to understand the difference:

When there’s a break statement and the condition is not met for the value "fifty", the code exits the while loop. However, when we use the continue statement, the execution of the while loop continues from the next item, which is 65.

Example 8: A while Loop with the else Clause

In Python, a while loop can be used with an else clause. When the condition in the while loop becomes false, the else block is executed. However, if there is a break statement inside the while loop block, the code exits the loop without executing the else block.

Let’s do an example to better understand this case:

This code searches for a name in the given names list. When the name is found, it prints “Name found!” and exits the loop. If the name is not found after going through all the names in the names list, the else block is executed, which prints “Name not found!”.

If we did not have the break statement inside the while loop, the code block would print both “Name found!” and “Name not found!” if the name exists in the list. Feel free to test it yourself.

Common while Mistakes and Tips

Python while loops are very useful for writing robust and efficient programs. However, there are some important points to keep in mind if you want to use them properly.

The biggest mistake is to forget about incrementing the loop variable – or not incrementing it correctly. Both may result in infinite loops or loops that do not function as expected. This might need extra attention, especially when working with nested loops.

Another tip: Do not overuse the break statement. Keep in mind that it exits the while loop entirely. If you place a break statement with an if condition, the while loop does not execute the remaining part. Recall the examples we have done on the break and continue statements. It’s better to use the continue statement if you want to complete the entire loop.

Need More Python while Loop Examples?

We learned Python while loops by solving 8 examples. Each example focused on a specific use case or particular component of the while loop. We have also learned the break and continue statements and how they improve the functionality of while loops.

To build your knowledge of while loops, keep practicing and solving more exercises. LearnPython.com offers several interactive online courses that will help you improve your Python skills. You can start with our three-course Python Basics track, which offers the opportunity to practice while learning Python programming from scratch. It contains 259 coding challenges.

If you want to practice working with Python data structures like lists, dictionaries, tuples, or sets, I recommend our course Python Data Structures in Practice . Happy learning!

Python Tutorial

File handling, python modules, python numpy, python pandas, python matplotlib, python scipy, machine learning, python mysql, python mongodb, python reference, module reference, python how to, python examples, python for loops.

A for loop is used for iterating over a sequence (that is either a list, a tuple, a dictionary, a set, or a string).

This is less like the for keyword in other programming languages, and works more like an iterator method as found in other object-orientated programming languages.

With the for loop we can execute a set of statements, once for each item in a list, tuple, set etc.

Print each fruit in a fruit list:

The for loop does not require an indexing variable to set beforehand.

Looping Through a String

Even strings are iterable objects, they contain a sequence of characters:

Loop through the letters in the word "banana":

The break Statement

With the break statement we can stop the loop before it has looped through all the items:

Exit the loop when x is "banana":

Exit the loop when x is "banana", but this time the break comes before the print:

The continue Statement

With the continue statement we can stop the current iteration of the loop, and continue with the next:

Do not print banana:

The range() Function

The range() function returns a sequence of numbers, starting from 0 by default, and increments by 1 (by default), and ends at a specified number.

Using the range() function:

Note that range(6) is not the values of 0 to 6, but the values 0 to 5.

The range() function defaults to 0 as a starting value, however it is possible to specify the starting value by adding a parameter: range(2, 6) , which means values from 2 to 6 (but not including 6):

Using the start parameter:

The range() function defaults to increment the sequence by 1, however it is possible to specify the increment value by adding a third parameter: range(2, 30, 3 ) :

Increment the sequence with 3 (default is 1):

Else in For Loop

The else keyword in a for loop specifies a block of code to be executed when the loop is finished:

Print all numbers from 0 to 5, and print a message when the loop has ended:

Note: The else block will NOT be executed if the loop is stopped by a break statement.

Break the loop when x is 3, and see what happens with the else block:

Nested Loops

A nested loop is a loop inside a loop.

The "inner loop" will be executed one time for each iteration of the "outer loop":

Print each adjective for every fruit:

The pass Statement

for loops cannot be empty, but if you for some reason have a for loop with no content, put in the pass statement to avoid getting an error.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Python Fundamentals

Python Variables and Literals
Python Type Conversion
Python Basic Input and Output
Python Operators

Python Flow Control

Python if...else Statement

Python for Loop

Python while Loop

Python break and continue

Python pass Statement

Python Data types

Python Numbers and Mathematics
Python List
Python Tuple
Python String
Python Dictionary
Python Functions
Python Function Arguments
Python Variable Scope
Python Global Keyword
Python Recursion
Python Modules
Python Package
Python Main function

Python Files

Python Directory and Files Management
Python CSV: Read and Write CSV files
Reading CSV files in Python
Writing CSV files in Python
Python Exception Handling
Python Exceptions
Python Custom Exceptions

Python Object & Class

Python Objects and Classes
Python Inheritance
Python Multiple Inheritance
Polymorphism in Python
Python Operator Overloading

Python Advanced Topics

List comprehension
Python Lambda/Anonymous Function
Python Iterators
Python Generators
Python Namespace and Scope
Python Closures
Python Decorators
Python @property decorator
Python RegEx

Python Date and Time

Python datetime
Python strftime()
Python strptime()
How to get current date and time in Python?
Python Get Current Time
Python timestamp to datetime and vice-versa
Python time Module
Python sleep()

Additional Topic

Precedence and Associativity of Operators in Python
Python Keywords and Identifiers
Python Asserts
Python Json
Python *args and **kwargs

Python Tutorials

Python Looping Techniques

Python range() Function

In Python, we use a while loop to repeat a block of code until a certain condition is met. For example,

In the above example, we have used a while loop to print the numbers from 1 to 3 . The loop runs as long as the condition number <= 3 is True .

while Loop Syntax
The while loop evaluates condition , which is a boolean expression.
If the condition is True , body of while loop is executed. The condition is evaluated again.
This process continues until the condition is False .
Once the condition evaluates to False , the loop terminates.

Tip: We should update the variables used in condition inside the loop so that it eventually evaluates to False . Otherwise, the loop keeps running, creating an infinite loop.

Flowchart of Python while Loop

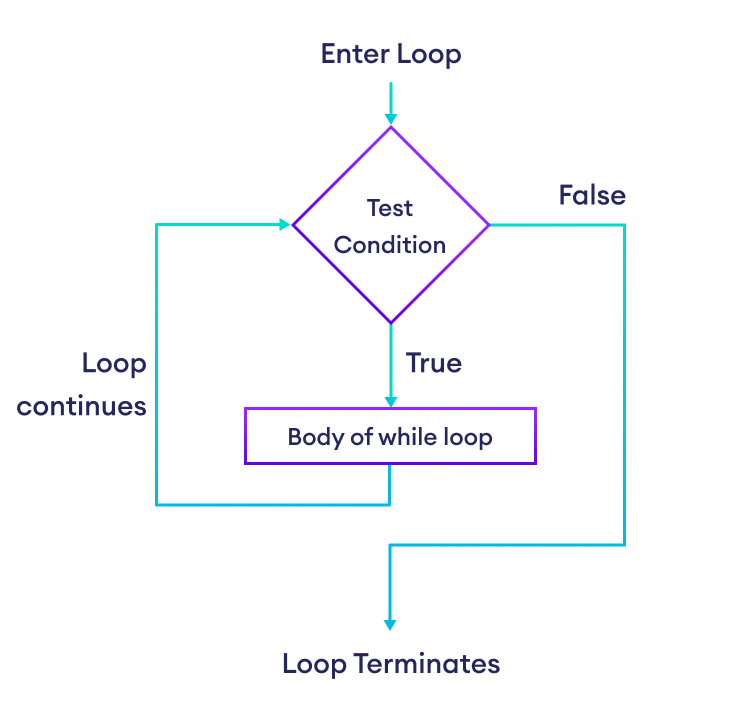
Example: Python while Loop

Here is how the above program works:

It asks the user to enter a number.
If the user enters a number other than 0 , it is printed.
If the user enters 0 , the loop terminates.
Infinite while Loop

If the condition of a while loop always evaluates to True , the loop runs continuously, forming an infinite while loop . For example,

The above program is equivalent to:

Video: Python while Loop

Sorry about that.

Assignment Operators in Python

The Python Operators are used to perform operations on values and variables. These are the special symbols that carry out arithmetic, logical, and bitwise computations. The value the operator operates on is known as the Operand. Here, we will cover Different Assignment operators in Python .


=	Assign the value of the right side of the expression to the left side operand	c = a + b
+=	Add right side operand with left side operand and then assign the result to left operand	a += b
-=	Subtract right side operand from left side operand and then assign the result to left operand	a -= b
*=	Multiply right operand with left operand and then assign the result to the left operand	a *= b
/=	Divide left operand with right operand and then assign the result to the left operand	a /= b
%=	Divides the left operand with the right operand and then assign the remainder to the left operand	a %= b
//=	Divide left operand with right operand and then assign the value(floor) to left operand	a //= b
**=	Calculate exponent(raise power) value using operands and then assign the result to left operand	a **= b
&=	Performs Bitwise AND on operands and assign the result to left operand	a &= b
\|=	Performs Bitwise OR on operands and assign the value to left operand	a \|= b
^=	Performs Bitwise XOR on operands and assign the value to left operand	a ^= b
>>=	Performs Bitwise right shift on operands and assign the result to left operand	a >>= b
<<=	Performs Bitwise left shift on operands and assign the result to left operand	a <<= b
:=	Assign a value to a variable within an expression	a := exp

Here are the Assignment Operators in Python with examples.

Assignment Operator

Assignment Operators are used to assign values to variables. This operator is used to assign the value of the right side of the expression to the left side operand.

Addition Assignment Operator

The Addition Assignment Operator is used to add the right-hand side operand with the left-hand side operand and then assigning the result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the addition assignment operator which will first perform the addition operation and then assign the result to the variable on the left-hand side.

S ubtraction Assignment Operator

The Subtraction Assignment Operator is used to subtract the right-hand side operand from the left-hand side operand and then assigning the result to the left-hand side operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the subtraction assignment operator which will first perform the subtraction operation and then assign the result to the variable on the left-hand side.

M ultiplication Assignment Operator

The Multiplication Assignment Operator is used to multiply the right-hand side operand with the left-hand side operand and then assigning the result to the left-hand side operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the multiplication assignment operator which will first perform the multiplication operation and then assign the result to the variable on the left-hand side.

D ivision Assignment Operator

The Division Assignment Operator is used to divide the left-hand side operand with the right-hand side operand and then assigning the result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the division assignment operator which will first perform the division operation and then assign the result to the variable on the left-hand side.

M odulus Assignment Operator

The Modulus Assignment Operator is used to take the modulus, that is, it first divides the operands and then takes the remainder and assigns it to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the modulus assignment operator which will first perform the modulus operation and then assign the result to the variable on the left-hand side.

F loor Division Assignment Operator

The Floor Division Assignment Operator is used to divide the left operand with the right operand and then assigs the result(floor value) to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the floor division assignment operator which will first perform the floor division operation and then assign the result to the variable on the left-hand side.

Exponentiation Assignment Operator

The Exponentiation Assignment Operator is used to calculate the exponent(raise power) value using operands and then assigning the result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the exponentiation assignment operator which will first perform exponent operation and then assign the result to the variable on the left-hand side.

Bitwise AND Assignment Operator

The Bitwise AND Assignment Operator is used to perform Bitwise AND operation on both operands and then assigning the result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the bitwise AND assignment operator which will first perform Bitwise AND operation and then assign the result to the variable on the left-hand side.

Bitwise OR Assignment Operator

The Bitwise OR Assignment Operator is used to perform Bitwise OR operation on the operands and then assigning result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the bitwise OR assignment operator which will first perform bitwise OR operation and then assign the result to the variable on the left-hand side.

Bitwise XOR Assignment Operator

The Bitwise XOR Assignment Operator is used to perform Bitwise XOR operation on the operands and then assigning result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the bitwise XOR assignment operator which will first perform bitwise XOR operation and then assign the result to the variable on the left-hand side.

Bitwise Right Shift Assignment Operator

The Bitwise Right Shift Assignment Operator is used to perform Bitwise Right Shift Operation on the operands and then assign result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the bitwise right shift assignment operator which will first perform bitwise right shift operation and then assign the result to the variable on the left-hand side.

Bitwise Left Shift Assignment Operator

The Bitwise Left Shift Assignment Operator is used to perform Bitwise Left Shift Opertator on the operands and then assign result to the left operand.

Example: In this code we have two variables ‘a’ and ‘b’ and assigned them with some integer value. Then we have used the bitwise left shift assignment operator which will first perform bitwise left shift operation and then assign the result to the variable on the left-hand side.

Walrus Operator

The Walrus Operator in Python is a new assignment operator which is introduced in Python version 3.8 and higher. This operator is used to assign a value to a variable within an expression.

Example: In this code, we have a Python list of integers. We have used Python Walrus assignment operator within the Python while loop . The operator will solve the expression on the right-hand side and assign the value to the left-hand side operand ‘x’ and then execute the remaining code.

Assignment Operators in Python – FAQs

What are assignment operators in python.

Assignment operators in Python are used to assign values to variables. These operators can also perform additional operations during the assignment. The basic assignment operator is = , which simply assigns the value of the right-hand operand to the left-hand operand. Other common assignment operators include += , -= , *= , /= , %= , and more, which perform an operation on the variable and then assign the result back to the variable.

What is the := Operator in Python?

The := operator, introduced in Python 3.8, is known as the “walrus operator”. It is an assignment expression, which means that it assigns values to variables as part of a larger expression. Its main benefit is that it allows you to assign values to variables within expressions, including within conditions of loops and if statements, thereby reducing the need for additional lines of code. Here’s an example: # Example of using the walrus operator in a while loop while (n := int(input("Enter a number (0 to stop): "))) != 0: print(f"You entered: {n}") This loop continues to prompt the user for input and immediately uses that input in both the condition check and the loop body.

What is the Assignment Operator in Structure?

In programming languages that use structures (like C or C++), the assignment operator = is used to copy values from one structure variable to another. Each member of the structure is copied from the source structure to the destination structure. Python, however, does not have a built-in concept of ‘structures’ as in C or C++; instead, similar functionality is achieved through classes or dictionaries.

What is the Assignment Operator in Python Dictionary?

In Python dictionaries, the assignment operator = is used to assign a new key-value pair to the dictionary or update the value of an existing key. Here’s how you might use it: my_dict = {} # Create an empty dictionary my_dict['key1'] = 'value1' # Assign a new key-value pair my_dict['key1'] = 'updated value' # Update the value of an existing key print(my_dict) # Output: {'key1': 'updated value'}

What is += and -= in Python?

The += and -= operators in Python are compound assignment operators. += adds the right-hand operand to the left-hand operand and assigns the result to the left-hand operand. Conversely, -= subtracts the right-hand operand from the left-hand operand and assigns the result to the left-hand operand. Here are examples of both: # Example of using += a = 5 a += 3 # Equivalent to a = a + 3 print(a) # Output: 8 # Example of using -= b = 10 b -= 4 # Equivalent to b = b - 4 print(b) # Output: 6 These operators make code more concise and are commonly used in loops and iterative data processing.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Assignment Expressions: The Walrus Operator

Discussion (8)

In this lesson, you’ll learn about the biggest change in Python 3.8: the introduction of assignment expressions . Assignment expression are written with a new notation (:=) .This operator is often called the walrus operator as it resembles the eyes and tusks of a walrus on its side.

Assignment expressions allow you to assign and return a value in the same expression. For example, if you want to assign to a variable and print its value, then you typically do something like this:

In Python 3.8, you’re allowed to combine these two statements into one, using the walrus operator:

The assignment expression allows you to assign True to walrus , and immediately print the value. But keep in mind that the walrus operator does not do anything that isn’t possible without it. It only makes certain constructs more convenient, and can sometimes communicate the intent of your code more clearly.

One pattern that shows some of the strengths of the walrus operator is while loops where you need to initialize and update a variable. For example, the following code asks the user for input until they type quit :

This code is less than ideal. You’re repeating the input() statement, and somehow you need to add current to the list before asking the user for it. A better solution is to set up an infinite while loop, and use break to stop the loop:

This code is equivalent to the code above, but avoids the repetition and somehow keeps the lines in a more logical order. If you use an assignment expression, then you can simplify this loop further:

This moves the test back to the while line, where it should be. However, there are now several things happening at that line, so it takes a bit more effort to read it properly. Use your best judgement about when the walrus operator helps make your code more readable.

PEP 572 describes all the details of assignment expressions, including some of the rationale for introducing them into the language, as well as several examples of how the walrus operator can be used. The Python 3.8 documentation also includes some good examples of assignment expressions.

Here are a few resources for more info on using bpython, the REPL (Read–Eval–Print Loop) tool used in most of these videos:

Discover bpython: A Python REPL With IDE-Like Features
A better Python REPL: bpython vs python
bpython Homepage
bpython Docs

00:00 In this video, you’ll learn about what’s being called the walrus operator. One of the biggest changes in Python 3.8 is the introduction of these assignment expressions. So, what does it do?

00:12 Well, it allows the assignment and the return of a value in the same expression, using a new notation. On the left side, you’d have the name of the object that you’re assigning, and then you have the operator, a colon and an equal sign ( := ), affectionately known as the walrus operator as it resembles the eyes and tusks of a walrus on its side.

00:32 And it’s assigning this expression on the right side, so it’s assigning and returning the value in the same expression. Let me have you practice with this operator with some code.

00:44 Throughout this tutorial, when I use a REPL, I’m going to be using this custom REPL called bpython . I’ll include links on how to install bpython below this video.

00:53 So, how do you use this assignment operator? Let me have you start with a small example. You could have an object named walrus and assign it the value of False , and then you could print it. In Python 3.8, you can combine those two statements and do a single statement using the walrus operator. So inside of print() , you could say walrus , the new object, and use the operator, the assignment expression := , and a space, and then say True . That’s going to do two things. Most notably, in reverse order, it returned the value True . And then it also assigned the value to walrus , and of course the type of 'bool' .

01:38 Keep in mind, the walrus operator doesn’t do anything that isn’t possible without it. It only makes certain constructs a bit more convenient, and can sometimes communicate the intent of your code more clearly.

01:48 Let me show you another example. It’s a pattern that shows some of the strengths of the walrus operator inside of while loops, where you need to initialize and update a variable. For example, create a new file, and name it write_something.py . Here’s write_something.py .

02:09 It starts with inputs , which will be a list. So create a list called inputs .

02:16 Into an object named current , use an input() statement. The input() statement is going to provide a prompt and read a string in from standard input. The prompt will be this, "Write something: " .

02:28 So when the user inputs that, that’ll go into current . So while current != "quit" — if the person has not typed quit yet— you’re going to take inputs and append the current value.

02:44 And then here, you’re asking to "Write something: " again.

02:50 Down here at my terminal, after saving—let’s see, make sure you’re saved. Okay. Now that’s saved.

03:00 So here, I could say, Hello , Welcome , and then finally quit , which then would quit it. So, this code isn’t ideal.

03:08 You’re repeating the input() statement twice, and somehow you need to add current to the list before asking the user for it. So a better solution is going to be to set up maybe an infinite while loop, and then use a break to stop the loop. How would that look?

03:22 You’re going to rearrange this a little bit. Move the while loop up, and say while True:

03:35 and here say if current == "quit": then break . Otherwise, go ahead and append it. So, a little different here, but this is a while loop that’s going to continue as long as it doesn’t get broken out of by someone typing quit . Okay.

03:53 Running it again. And there, you can see it breaking out. Nice. So, that code avoids the repetition and kind of keeps things in a more logical order, but there’s a way to simplify this to use that new assignment expression, the walrus operator. In that case, you’re going to modify this quite a bit.

04:17 Here you’re going to say while , current and then use that assignment operator ( := ) to create current .

04:23 But also, while doing that, check to see that it’s not equal to "quit" . So here, each time that assigns the value to current and it’s returned, so the value can be checked.

04:35 So while , current , assigning the value from the input() , and then if it’s not equal to "quit" , you’re going to append current . Make sure to save.

04:42 Run the code one more time.

04:47 And it works the same. This moves that test all the way back to the while line, where it should be. However, there’s a couple of things now happening all in one line, and that might take a little more effort to read what’s happening and to understand it properly.

05:00 There are a handful of other examples that you could look into to learn a little more about assignment expressions. I’ll include a link to PEP 572, and also a link to the Python docs for version 3.8, both of which include more code examples.

05:14 So you need to use your best judgment as to when this operator’s going to make your code more readable and more useful. In the next video, you’ll learn about the new feature of positional-only arguments.

rajeshboyalla on Dec. 4, 2019

Why do you use list() to initialize a list rather than using [] ?

Geir Arne Hjelle RP Team on Dec. 4, 2019

My two cents about list() vs [] (I wrote the original article this video series is based on):

I find spelling out list() to be more readable and easier to notice and interpret than []
[] is several times faster than list() , but we’re still talking nanoseconds. On my computer [] takes about 15ns, while list() runs in 60ns. Typically, lists are initiated once, so this does not cause any meaningful slowdown of code.

That said, if I’m initializing a list with existing elements, I usually use [elem1, elem2, ...] , since list(...) has different–and sometimes surprising–semantics.

Jason on April 3, 2020

Sorry for my ignorance, did the the standard assignment = operator work in this way? I don’t understand what has been gained from adding the := operator. If anything I think it will allow people to write more obfuscated code. But minds better than mine have been working on this, so I’ll have to take their word it is an improvement.

As for the discussion on whether [] is more readable than list(). I’d never seen list() before, so to me [] is better. I’ve only just come over from the dark 2.7 side so maybe it’s an old python programmer thing?

Oh I checked the operation on the assignment operator. I was obviously wrong. lol Still I think the existing operator could’ve been tweaked to do the same thing as := … I’m still on the fence about that one.

gedece on April 3, 2020

you are right in that the existing operator could have worked, but it can lead to something unexpected.

if you do something like

if (newvar = somevar): it gives a traceback, because you are supposed to use == for comparations.

So if you use the normal operator for this, then that expression is valid and you’ll be hard pressed to realize the mistake.

It then makes complete sense to use a different operator as that helps to clarify intent in code.

Jason on April 6, 2020

Yes, I’ve accidentaly done that in other languages before and it can be a difficult to “see” bug.

varelaautumn on Sept. 26, 2020

I watched this earlier today and now tonight I just can’t stop myself from throwing these walrus operators everywhere.

(I’m new and learning so these are just personal fooling around programs)

For example I have this function which cycles through a bunch of other very simple parsing functions that check if my input string is valid in the context of the game state. If the string doesn’t pass one of these parsers it returns a string with an error message such as “Input must be less than 5 characters”. And then the parse_input function returns that error string.

I mean it’s not a huge change, but it saves an extra call of the function, and I feel like it makes it much more readable.

I’m not sure if this other case might be considered abuse of the walrus operator, but I decided to use it twice in one line.

This function repeatedly asks for input. If the input does not pass the parser functions, then the error will be returned and printed out in the while loop. Otherwise the input was valid and it gets returned.

I’m able to pass my input into a function and check the result of that function all while retaining my input and the return of the function as their own variables to be used in the next line.

I think the walrus operator helped me put all the relevant details on the three lines. Like if you just read the first words of each line, it basically says “while error, print error, else return input_string.” I don’t see how I could have done that without this cool walrus operator so I’m really appreciative for this video you made! I’ve been converted to a strong believer in the walrus operator.

Geir Arne Hjelle RP Team on Sept. 26, 2020

@varelaautumn Nice examples, thanks for sharing!

I agree that the walrus operator will not revolutionize your code, but it can bring these sorts of small improvements that add up in the long run.

Become a Member to join the conversation.

18 Python while Loop Examples and Exercises

In Python programming, we use while loops to do a task a certain number of times repeatedly. The while loop checks a condition and executes the task as long as that condition is satisfied. The loop will stop its execution once the condition becomes not satisfied.

1. Example of using while loops in Python

2. example of using the break statement in while loops.

In Python, we can use the break statement to end a while loop prematurely.

3. Example of using the continue statement in while loops

4. using if-elif-else statements inside while loop, 5. adding elements to a list using while loop, 6. python while loop to print a number series, 7. printing the items in a tuple using while loop, 8. finding the sum of numbers in a list using while loop, 9. popping out elements from a list using while loop, 10. printing all letters except some using python while loop, 11. python while loop to take inputs from the user, 12. converting numbers from decimal to binary using while loop, 13. finding the average of 5 numbers using while loop, 14. printing the square of numbers using while loop, 15. finding the multiples of a number using while loop, 16. reversing a number using while loop in python, 17. finding the sum of even numbers using while loop, 18. finding the factorial of a given number using while loop.

I hope this article was helpful. Check out my post on 21 Python for Loop Examples .

16 thoughts on “ 18 Python while Loop Examples and Exercises ”

I am looking for a way to take user inputs in while loop & compare it & print the smallest/largest value. Can you help?

Write a program that reads a value V, and then starts to read further values and adds them to a List until the initial value V is added again. Don’t add the first V and last V to the list. Print the list to the console.

print(f”The given list of numerical entities is formed by {internal_list}”) if i >= x: print(f”The maximal value contained by user’ list is equal with… {max(internal_list)}”) else: pass

i=0 newlist=[] #create an empty list while i<5: #for 5 values x=int(input(' Enter numbers')) i+=1 newlist.append(x) print(newlist) #you may skip this line print("The smallest number is", min(newlist))

Printing the items in a tuple using while loop exercise shows wrong answer please review the answer.

# Now i want to see both methods while and for to striped out the strip’s values from the name’s letters.

Rony its true but what do you mean by write coments on your code

4.1. if Statements ¶

Perhaps the most well-known statement type is the if statement. For example:

There can be zero or more elif parts, and the else part is optional. The keyword ‘ elif ’ is short for ‘else if’, and is useful to avoid excessive indentation. An if … elif … elif … sequence is a substitute for the switch or case statements found in other languages.

If you’re comparing the same value to several constants, or checking for specific types or attributes, you may also find the match statement useful. For more details see match Statements .

4.2. for Statements ¶

The for statement in Python differs a bit from what you may be used to in C or Pascal. Rather than always iterating over an arithmetic progression of numbers (like in Pascal), or giving the user the ability to define both the iteration step and halting condition (as C), Python’s for statement iterates over the items of any sequence (a list or a string), in the order that they appear in the sequence. For example (no pun intended):

Code that modifies a collection while iterating over that same collection can be tricky to get right. Instead, it is usually more straight-forward to loop over a copy of the collection or to create a new collection:

4.3. The range() Function ¶

If you do need to iterate over a sequence of numbers, the built-in function range() comes in handy. It generates arithmetic progressions:

The given end point is never part of the generated sequence; range(10) generates 10 values, the legal indices for items of a sequence of length 10. It is possible to let the range start at another number, or to specify a different increment (even negative; sometimes this is called the ‘step’):

To iterate over the indices of a sequence, you can combine range() and len() as follows:

In most such cases, however, it is convenient to use the enumerate() function, see Looping Techniques .

A strange thing happens if you just print a range:

In many ways the object returned by range() behaves as if it is a list, but in fact it isn’t. It is an object which returns the successive items of the desired sequence when you iterate over it, but it doesn’t really make the list, thus saving space.

We say such an object is iterable , that is, suitable as a target for functions and constructs that expect something from which they can obtain successive items until the supply is exhausted. We have seen that the for statement is such a construct, while an example of a function that takes an iterable is sum() :

Later we will see more functions that return iterables and take iterables as arguments. In chapter Data Structures , we will discuss in more detail about list() .

4.4. break and continue Statements, and else Clauses on Loops ¶

The break statement breaks out of the innermost enclosing for or while loop.

A for or while loop can include an else clause.

In a for loop, the else clause is executed after the loop reaches its final iteration.

In a while loop, it’s executed after the loop’s condition becomes false.

In either kind of loop, the else clause is not executed if the loop was terminated by a break .

This is exemplified in the following for loop, which searches for prime numbers:

(Yes, this is the correct code. Look closely: the else clause belongs to the for loop, not the if statement.)

When used with a loop, the else clause has more in common with the else clause of a try statement than it does with that of if statements: a try statement’s else clause runs when no exception occurs, and a loop’s else clause runs when no break occurs. For more on the try statement and exceptions, see Handling Exceptions .

The continue statement, also borrowed from C, continues with the next iteration of the loop:

4.5. pass Statements ¶

The pass statement does nothing. It can be used when a statement is required syntactically but the program requires no action. For example:

This is commonly used for creating minimal classes:

Another place pass can be used is as a place-holder for a function or conditional body when you are working on new code, allowing you to keep thinking at a more abstract level. The pass is silently ignored:

4.6. match Statements ¶

A match statement takes an expression and compares its value to successive patterns given as one or more case blocks. This is superficially similar to a switch statement in C, Java or JavaScript (and many other languages), but it’s more similar to pattern matching in languages like Rust or Haskell. Only the first pattern that matches gets executed and it can also extract components (sequence elements or object attributes) from the value into variables.

The simplest form compares a subject value against one or more literals:

Note the last block: the “variable name” _ acts as a wildcard and never fails to match. If no case matches, none of the branches is executed.

You can combine several literals in a single pattern using | (“or”):

Patterns can look like unpacking assignments, and can be used to bind variables:

Study that one carefully! The first pattern has two literals, and can be thought of as an extension of the literal pattern shown above. But the next two patterns combine a literal and a variable, and the variable binds a value from the subject ( point ). The fourth pattern captures two values, which makes it conceptually similar to the unpacking assignment (x, y) = point .

If you are using classes to structure your data you can use the class name followed by an argument list resembling a constructor, but with the ability to capture attributes into variables:

You can use positional parameters with some builtin classes that provide an ordering for their attributes (e.g. dataclasses). You can also define a specific position for attributes in patterns by setting the __match_args__ special attribute in your classes. If it’s set to (“x”, “y”), the following patterns are all equivalent (and all bind the y attribute to the var variable):

A recommended way to read patterns is to look at them as an extended form of what you would put on the left of an assignment, to understand which variables would be set to what. Only the standalone names (like var above) are assigned to by a match statement. Dotted names (like foo.bar ), attribute names (the x= and y= above) or class names (recognized by the “(…)” next to them like Point above) are never assigned to.

Patterns can be arbitrarily nested. For example, if we have a short list of Points, with __match_args__ added, we could match it like this:

We can add an if clause to a pattern, known as a “guard”. If the guard is false, match goes on to try the next case block. Note that value capture happens before the guard is evaluated:

Several other key features of this statement:

Like unpacking assignments, tuple and list patterns have exactly the same meaning and actually match arbitrary sequences. An important exception is that they don’t match iterators or strings.

Sequence patterns support extended unpacking: [x, y, *rest] and (x, y, *rest) work similar to unpacking assignments. The name after * may also be _ , so (x, y, *_) matches a sequence of at least two items without binding the remaining items.

Mapping patterns: {"bandwidth": b, "latency": l} captures the "bandwidth" and "latency" values from a dictionary. Unlike sequence patterns, extra keys are ignored. An unpacking like **rest is also supported. (But **_ would be redundant, so it is not allowed.)

Subpatterns may be captured using the as keyword:

will capture the second element of the input as p2 (as long as the input is a sequence of two points)

Most literals are compared by equality, however the singletons True , False and None are compared by identity.

Patterns may use named constants. These must be dotted names to prevent them from being interpreted as capture variable:

For a more detailed explanation and additional examples, you can look into PEP 636 which is written in a tutorial format.

4.7. Defining Functions ¶

We can create a function that writes the Fibonacci series to an arbitrary boundary:

The keyword def introduces a function definition . It must be followed by the function name and the parenthesized list of formal parameters. The statements that form the body of the function start at the next line, and must be indented.

The first statement of the function body can optionally be a string literal; this string literal is the function’s documentation string, or docstring . (More about docstrings can be found in the section Documentation Strings .) There are tools which use docstrings to automatically produce online or printed documentation, or to let the user interactively browse through code; it’s good practice to include docstrings in code that you write, so make a habit of it.

The execution of a function introduces a new symbol table used for the local variables of the function. More precisely, all variable assignments in a function store the value in the local symbol table; whereas variable references first look in the local symbol table, then in the local symbol tables of enclosing functions, then in the global symbol table, and finally in the table of built-in names. Thus, global variables and variables of enclosing functions cannot be directly assigned a value within a function (unless, for global variables, named in a global statement, or, for variables of enclosing functions, named in a nonlocal statement), although they may be referenced.

The actual parameters (arguments) to a function call are introduced in the local symbol table of the called function when it is called; thus, arguments are passed using call by value (where the value is always an object reference , not the value of the object). [ 1 ] When a function calls another function, or calls itself recursively, a new local symbol table is created for that call.

A function definition associates the function name with the function object in the current symbol table. The interpreter recognizes the object pointed to by that name as a user-defined function. Other names can also point to that same function object and can also be used to access the function:

Coming from other languages, you might object that fib is not a function but a procedure since it doesn’t return a value. In fact, even functions without a return statement do return a value, albeit a rather boring one. This value is called None (it’s a built-in name). Writing the value None is normally suppressed by the interpreter if it would be the only value written. You can see it if you really want to using print() :

It is simple to write a function that returns a list of the numbers of the Fibonacci series, instead of printing it:

This example, as usual, demonstrates some new Python features:

The return statement returns with a value from a function. return without an expression argument returns None . Falling off the end of a function also returns None .

The statement result.append(a) calls a method of the list object result . A method is a function that ‘belongs’ to an object and is named obj.methodname , where obj is some object (this may be an expression), and methodname is the name of a method that is defined by the object’s type. Different types define different methods. Methods of different types may have the same name without causing ambiguity. (It is possible to define your own object types and methods, using classes , see Classes ) The method append() shown in the example is defined for list objects; it adds a new element at the end of the list. In this example it is equivalent to result = result + [a] , but more efficient.

4.8. More on Defining Functions ¶

It is also possible to define functions with a variable number of arguments. There are three forms, which can be combined.

4.8.1. Default Argument Values ¶

The most useful form is to specify a default value for one or more arguments. This creates a function that can be called with fewer arguments than it is defined to allow. For example:

This function can be called in several ways:

giving only the mandatory argument: ask_ok('Do you really want to quit?')

giving one of the optional arguments: ask_ok('OK to overwrite the file?', 2)

or even giving all arguments: ask_ok('OK to overwrite the file?', 2, 'Come on, only yes or no!')

This example also introduces the in keyword. This tests whether or not a sequence contains a certain value.

The default values are evaluated at the point of function definition in the defining scope, so that

will print 5 .

Important warning: The default value is evaluated only once. This makes a difference when the default is a mutable object such as a list, dictionary, or instances of most classes. For example, the following function accumulates the arguments passed to it on subsequent calls:

This will print

If you don’t want the default to be shared between subsequent calls, you can write the function like this instead:

4.8.2. Keyword Arguments ¶

Functions can also be called using keyword arguments of the form kwarg=value . For instance, the following function:

accepts one required argument ( voltage ) and three optional arguments ( state , action , and type ). This function can be called in any of the following ways:

but all the following calls would be invalid:

In a function call, keyword arguments must follow positional arguments. All the keyword arguments passed must match one of the arguments accepted by the function (e.g. actor is not a valid argument for the parrot function), and their order is not important. This also includes non-optional arguments (e.g. parrot(voltage=1000) is valid too). No argument may receive a value more than once. Here’s an example that fails due to this restriction:

When a final formal parameter of the form **name is present, it receives a dictionary (see Mapping Types — dict ) containing all keyword arguments except for those corresponding to a formal parameter. This may be combined with a formal parameter of the form *name (described in the next subsection) which receives a tuple containing the positional arguments beyond the formal parameter list. ( *name must occur before **name .) For example, if we define a function like this:

It could be called like this:

and of course it would print:

Note that the order in which the keyword arguments are printed is guaranteed to match the order in which they were provided in the function call.

4.8.3. Special parameters ¶

By default, arguments may be passed to a Python function either by position or explicitly by keyword. For readability and performance, it makes sense to restrict the way arguments can be passed so that a developer need only look at the function definition to determine if items are passed by position, by position or keyword, or by keyword.

A function definition may look like:

where / and * are optional. If used, these symbols indicate the kind of parameter by how the arguments may be passed to the function: positional-only, positional-or-keyword, and keyword-only. Keyword parameters are also referred to as named parameters.

4.8.3.1. Positional-or-Keyword Arguments ¶

If / and * are not present in the function definition, arguments may be passed to a function by position or by keyword.

4.8.3.2. Positional-Only Parameters ¶

Looking at this in a bit more detail, it is possible to mark certain parameters as positional-only . If positional-only , the parameters’ order matters, and the parameters cannot be passed by keyword. Positional-only parameters are placed before a / (forward-slash). The / is used to logically separate the positional-only parameters from the rest of the parameters. If there is no / in the function definition, there are no positional-only parameters.

Parameters following the / may be positional-or-keyword or keyword-only .

4.8.3.3. Keyword-Only Arguments ¶

To mark parameters as keyword-only , indicating the parameters must be passed by keyword argument, place an * in the arguments list just before the first keyword-only parameter.

4.8.3.4. Function Examples ¶

Consider the following example function definitions paying close attention to the markers / and * :

The first function definition, standard_arg , the most familiar form, places no restrictions on the calling convention and arguments may be passed by position or keyword:

The second function pos_only_arg is restricted to only use positional parameters as there is a / in the function definition:

The third function kwd_only_args only allows keyword arguments as indicated by a * in the function definition:

And the last uses all three calling conventions in the same function definition:

Finally, consider this function definition which has a potential collision between the positional argument name and **kwds which has name as a key:

There is no possible call that will make it return True as the keyword 'name' will always bind to the first parameter. For example:

But using / (positional only arguments), it is possible since it allows name as a positional argument and 'name' as a key in the keyword arguments:

In other words, the names of positional-only parameters can be used in **kwds without ambiguity.

4.8.3.5. Recap ¶

The use case will determine which parameters to use in the function definition:

As guidance:

Use positional-only if you want the name of the parameters to not be available to the user. This is useful when parameter names have no real meaning, if you want to enforce the order of the arguments when the function is called or if you need to take some positional parameters and arbitrary keywords.

Use keyword-only when names have meaning and the function definition is more understandable by being explicit with names or you want to prevent users relying on the position of the argument being passed.

For an API, use positional-only to prevent breaking API changes if the parameter’s name is modified in the future.

4.8.4. Arbitrary Argument Lists ¶

Finally, the least frequently used option is to specify that a function can be called with an arbitrary number of arguments. These arguments will be wrapped up in a tuple (see Tuples and Sequences ). Before the variable number of arguments, zero or more normal arguments may occur.

Normally, these variadic arguments will be last in the list of formal parameters, because they scoop up all remaining input arguments that are passed to the function. Any formal parameters which occur after the *args parameter are ‘keyword-only’ arguments, meaning that they can only be used as keywords rather than positional arguments.

4.8.5. Unpacking Argument Lists ¶

The reverse situation occurs when the arguments are already in a list or tuple but need to be unpacked for a function call requiring separate positional arguments. For instance, the built-in range() function expects separate start and stop arguments. If they are not available separately, write the function call with the * -operator to unpack the arguments out of a list or tuple:

In the same fashion, dictionaries can deliver keyword arguments with the ** -operator:

4.8.6. Lambda Expressions ¶

Small anonymous functions can be created with the lambda keyword. This function returns the sum of its two arguments: lambda a, b: a+b . Lambda functions can be used wherever function objects are required. They are syntactically restricted to a single expression. Semantically, they are just syntactic sugar for a normal function definition. Like nested function definitions, lambda functions can reference variables from the containing scope:

The above example uses a lambda expression to return a function. Another use is to pass a small function as an argument:

4.8.7. Documentation Strings ¶

Here are some conventions about the content and formatting of documentation strings.

The first line should always be a short, concise summary of the object’s purpose. For brevity, it should not explicitly state the object’s name or type, since these are available by other means (except if the name happens to be a verb describing a function’s operation). This line should begin with a capital letter and end with a period.

If there are more lines in the documentation string, the second line should be blank, visually separating the summary from the rest of the description. The following lines should be one or more paragraphs describing the object’s calling conventions, its side effects, etc.

The Python parser does not strip indentation from multi-line string literals in Python, so tools that process documentation have to strip indentation if desired. This is done using the following convention. The first non-blank line after the first line of the string determines the amount of indentation for the entire documentation string. (We can’t use the first line since it is generally adjacent to the string’s opening quotes so its indentation is not apparent in the string literal.) Whitespace “equivalent” to this indentation is then stripped from the start of all lines of the string. Lines that are indented less should not occur, but if they occur all their leading whitespace should be stripped. Equivalence of whitespace should be tested after expansion of tabs (to 8 spaces, normally).

Here is an example of a multi-line docstring:

4.8.8. Function Annotations ¶

Function annotations are completely optional metadata information about the types used by user-defined functions (see PEP 3107 and PEP 484 for more information).

Annotations are stored in the __annotations__ attribute of the function as a dictionary and have no effect on any other part of the function. Parameter annotations are defined by a colon after the parameter name, followed by an expression evaluating to the value of the annotation. Return annotations are defined by a literal -> , followed by an expression, between the parameter list and the colon denoting the end of the def statement. The following example has a required argument, an optional argument, and the return value annotated:

4.9. Intermezzo: Coding Style ¶

Now that you are about to write longer, more complex pieces of Python, it is a good time to talk about coding style . Most languages can be written (or more concise, formatted ) in different styles; some are more readable than others. Making it easy for others to read your code is always a good idea, and adopting a nice coding style helps tremendously for that.

For Python, PEP 8 has emerged as the style guide that most projects adhere to; it promotes a very readable and eye-pleasing coding style. Every Python developer should read it at some point; here are the most important points extracted for you:

Use 4-space indentation, and no tabs.

4 spaces are a good compromise between small indentation (allows greater nesting depth) and large indentation (easier to read). Tabs introduce confusion, and are best left out.

Wrap lines so that they don’t exceed 79 characters.

This helps users with small displays and makes it possible to have several code files side-by-side on larger displays.

Use blank lines to separate functions and classes, and larger blocks of code inside functions.

When possible, put comments on a line of their own.

Use docstrings.

Use spaces around operators and after commas, but not directly inside bracketing constructs: a = f(1, 2) + g(3, 4) .

Name your classes and functions consistently; the convention is to use UpperCamelCase for classes and lowercase_with_underscores for functions and methods. Always use self as the name for the first method argument (see A First Look at Classes for more on classes and methods).

Don’t use fancy encodings if your code is meant to be used in international environments. Python’s default, UTF-8, or even plain ASCII work best in any case.

Likewise, don’t use non-ASCII characters in identifiers if there is only the slightest chance people speaking a different language will read or maintain the code.

4.1. if Statements
4.2. for Statements
4.3. The range() Function
4.4. break and continue Statements, and else Clauses on Loops
4.5. pass Statements
4.6. match Statements
4.7. Defining Functions
4.8.1. Default Argument Values
4.8.2. Keyword Arguments
4.8.3.1. Positional-or-Keyword Arguments
4.8.3.2. Positional-Only Parameters
4.8.3.3. Keyword-Only Arguments
4.8.3.4. Function Examples
4.8.3.5. Recap
4.8.4. Arbitrary Argument Lists
4.8.5. Unpacking Argument Lists
4.8.6. Lambda Expressions
4.8.7. Documentation Strings
4.8.8. Function Annotations
4.9. Intermezzo: Coding Style

Previous topic

3. An Informal Introduction to Python

5. Data Structures

Report a Bug
Show Source

Python Programming

Practice Python Exercises and Challenges with Solutions

Free Coding Exercises for Python Developers. Exercises cover Python Basics , Data structure , to Data analytics . As of now, this page contains 18 Exercises.

What included in these Python Exercises?

Each exercise contains specific Python topic questions you need to practice and solve. These free exercises are nothing but Python assignments for the practice where you need to solve different programs and challenges.

All exercises are tested on Python 3.
Each exercise has 10-20 Questions.
The solution is provided for every question.
Practice each Exercise in Online Code Editor

These Python programming exercises are suitable for all Python developers. If you are a beginner, you will have a better understanding of Python after solving these exercises. Below is the list of exercises.

Select the exercise you want to solve .

Basic Exercise for Beginners

Practice and Quickly learn Python’s necessary skills by solving simple questions and problems.

Topics : Variables, Operators, Loops, String, Numbers, List

Python Input and Output Exercise

Solve input and output operations in Python. Also, we practice file handling.

Topics : print() and input() , File I/O

Python Loop Exercise

This Python loop exercise aims to help developers to practice branching and Looping techniques in Python.

Topics : If-else statements, loop, and while loop.

Python Functions Exercise

Practice how to create a function, nested functions, and use the function arguments effectively in Python by solving different questions.

Topics : Functions arguments, built-in functions.

Python String Exercise

Solve Python String exercise to learn and practice String operations and manipulations.

Python Data Structure Exercise

Practice widely used Python types such as List, Set, Dictionary, and Tuple operations in Python

Python List Exercise

This Python list exercise aims to help Python developers to learn and practice list operations.

Python Dictionary Exercise

This Python dictionary exercise aims to help Python developers to learn and practice dictionary operations.

Python Set Exercise

This exercise aims to help Python developers to learn and practice set operations.

Python Tuple Exercise

This exercise aims to help Python developers to learn and practice tuple operations.

Python Date and Time Exercise

This exercise aims to help Python developers to learn and practice DateTime and timestamp questions and problems.

Topics : Date, time, DateTime, Calendar.

Python OOP Exercise

This Python Object-oriented programming (OOP) exercise aims to help Python developers to learn and practice OOP concepts.

Topics : Object, Classes, Inheritance

Python JSON Exercise

Practice and Learn JSON creation, manipulation, Encoding, Decoding, and parsing using Python

Python NumPy Exercise

Practice NumPy questions such as Array manipulations, numeric ranges, Slicing, indexing, Searching, Sorting, and splitting, and more.

Python Pandas Exercise

Practice Data Analysis using Python Pandas. Practice Data-frame, Data selection, group-by, Series, sorting, searching, and statistics.

Python Matplotlib Exercise

Practice Data visualization using Python Matplotlib. Line plot, Style properties, multi-line plot, scatter plot, bar chart, histogram, Pie chart, Subplot, stack plot.

Random Data Generation Exercise

Practice and Learn the various techniques to generate random data in Python.

Topics : random module, secrets module, UUID module

Python Database Exercise

Practice Python database programming skills by solving the questions step by step.

Use any of the MySQL, PostgreSQL, SQLite to solve the exercise

Exercises for Intermediate developers

The following practice questions are for intermediate Python developers.

If you have not solved the above exercises, please complete them to understand and practice each topic in detail. After that, you can solve the below questions quickly.

Exercise 1: Reverse each word of a string

Expected Output

Use the split() method to split a string into a list of words.
Reverse each word from a list
finally, use the join() function to convert a list into a string

Steps to solve this question :

Split the given string into a list of words using the split() method
Use a list comprehension to create a new list by reversing each word from a list.
Use the join() function to convert the new list into a string
Display the resultant string

Exercise 2: Read text file into a variable and replace all newlines with space

Given : Assume you have a following text file (sample.txt).

Expected Output :

First, read a text file.
Next, use string replace() function to replace all newlines ( \n ) with space ( ' ' ).

Steps to solve this question : -

First, open the file in a read mode
Next, read all content from a file using the read() function and assign it to a variable.
Display final string

Exercise 3: Remove items from a list while iterating

Description :

In this question, You need to remove items from a list while iterating but without creating a different copy of a list.

Remove numbers greater than 50

Expected Output : -

Get the list's size
Iterate list using while loop
Check if the number is greater than 50
If yes, delete the item using a del keyword
Reduce the list size

Solution 1: Using while loop

Solution 2: Using for loop and range()

Exercise 4: Reverse Dictionary mapping

Exercise 5: display all duplicate items from a list.

Use the counter() method of the collection module.
Create a dictionary that will maintain the count of each item of a list. Next, Fetch all keys whose value is greater than 2

Solution 1 : - Using collections.Counter()

Solution 2 : -

Exercise 6: Filter dictionary to contain keys present in the given list

Exercise 7: print the following number pattern.

Refer to Print patterns in Python to solve this question.

Use two for loops
The outer loop is reverse for loop from 5 to 0
Increment value of x by 1 in each iteration of an outer loop
The inner loop will iterate from 0 to the value of i of the outer loop
Print value of x in each iteration of an inner loop
Print newline at the end of each outer loop

Exercise 8: Create an inner function

Question description : -

Create an outer function that will accept two strings, x and y . ( x= 'Emma' and y = 'Kelly' .
Create an inner function inside an outer function that will concatenate x and y.
At last, an outer function will join the word 'developer' to it.

Exercise 9: Modify the element of a nested list inside the following list

Change the element 35 to 3500

Exercise 10: Access the nested key increment from the following dictionary

Under Exercises: -

Python Object-Oriented Programming (OOP) Exercise: Classes and Objects Exercises

Updated on: December 8, 2021 | 52 Comments

Python Date and Time Exercise with Solutions

Updated on: December 8, 2021 | 10 Comments

Python Dictionary Exercise with Solutions

Updated on: May 6, 2023 | 56 Comments

Python Tuple Exercise with Solutions

Updated on: December 8, 2021 | 96 Comments

Python Set Exercise with Solutions

Updated on: October 20, 2022 | 27 Comments

Python if else, for loop, and range() Exercises with Solutions

Updated on: July 6, 2024 | 296 Comments

Updated on: August 2, 2022 | 155 Comments

Updated on: September 6, 2021 | 109 Comments

Python List Exercise with Solutions

Updated on: December 8, 2021 | 200 Comments

Updated on: December 8, 2021 | 7 Comments

Python Data Structure Exercise for Beginners

Updated on: December 8, 2021 | 116 Comments

Python String Exercise with Solutions

Updated on: October 6, 2021 | 221 Comments

Updated on: March 9, 2021 | 23 Comments

Updated on: March 9, 2021 | 51 Comments

Updated on: July 20, 2021 | 29 Comments

Python Basic Exercise for Beginners

Updated on: August 31, 2023 | 497 Comments

Useful Python Tips and Tricks Every Programmer Should Know

Updated on: May 17, 2021 | 23 Comments

Python random Data generation Exercise

Updated on: December 8, 2021 | 13 Comments

Python Database Programming Exercise

Updated on: March 9, 2021 | 17 Comments

Online Python Code Editor

Updated on: June 1, 2022 |

About PYnative

PYnative.com is for Python lovers. Here, You can get Tutorials, Exercises, and Quizzes to practice and improve your Python skills .

Explore Python

Learn Python
Python Basics
Python Databases
Python Exercises
Python Quizzes
Python Tricks

To get New Python Tutorials, Exercises, and Quizzes

Legal Stuff

We use cookies to improve your experience. While using PYnative, you agree to have read and accepted our Terms Of Use , Cookie Policy , and Privacy Policy .

Efficient estimation of the modified Gromov–Hausdorff distance between unweighted graphs

Open access
Published: 23 August 2024
Volume 48 , article number 14 , ( 2024 )

Cite this article

You have full access to this open access article

Vladyslav Oles ORCID: orcid.org/0000-0001-8872-7463 1 ,
Nathan Lemons 1 &
Alexander Panchenko 1

Gromov–Hausdorff distances measure shape difference between the objects representable as compact metric spaces, e.g. point clouds, manifolds, or graphs. Computing any Gromov–Hausdorff distance is equivalent to solving an NP-hard optimization problem, deeming the notion impractical for applications. In this paper we propose a polynomial algorithm for estimating the so-called modified Gromov–Hausdorff (mGH) distance, a relaxation of the standard Gromov–Hausdorff (GH) distance with similar topological properties. We implement the algorithm for the case of compact metric spaces induced by unweighted graphs as part of Python library scikit-tda , and demonstrate its performance on real-world and synthetic networks. The algorithm finds the mGH distances exactly on most graphs with the scale-free property. We use the computed mGH distances to successfully detect outliers in real-world social and computer networks.

Avoid common mistakes on your manuscript.

1 Introduction

1.1 isometry-invariant distances between metric spaces.

The Gromov–Hausdorff (GH) distance, proposed by Gromov in Gromov ( 1981 ) (see also Tuzhilin ( 2016 )), measures how far two compact metric spaces are from being isometric to each other. Since its conception four decades ago, the GH distance was mainly studied from a theoretical standpoint, as its computation poses an intractable combinatorial problem (Chazal et al. 2009 ; Mémoli 2007 ; Schmiedl 2017 ). Computing the GH distance can be thought of as an extension of the NP-hard Quadratic Bottleneck Assignment Problem (QBAP) that allows non-injective assignments in its search space. In particular, it was shown that approximating the distance up to a factor of $\sqrt{N}$ in the general case (or up to a factor of 3 for ultrametric spaces or metric trees) cannot be done in polynomial time unless $\text {P}=\text {NP}$ (Schmiedl 2017 ; Pankaj K et al. 2018 ). However, a polynomial-time algorithm for $\sqrt{N}$ -approximation was given for unweighted metric trees in Pankaj K et al. ( 2018 ), and a superlinear $\frac{5}{4}$ -approximation algorithm for subsets of $\mathbb {R}^1$ was derived in Majhi et al. ( 2016 ). In Mémoli and Sapiro ( 2004 ), the GH distance was first considered for shape comparison, and several of its computationally motivated relaxations were presented since then.

Different variations of the Gromov–Wasserstein distance, a relaxation of the GH distance for metric measure spaces motivated by the optimal transport problem (Villani 2003 ), were proposed in Sturm ( 2006 ) and in Mémoli ( 2007 ), and further studied in e.g. Mémoli ( 2009 ), Mémoli ( 2011 ), Peyré et al. ( 2016 ). The Gromov–Wasserstein distances are based on a generalization of bijective assignments, which are less expressive than the assignments allowed in the GH distance. Similarly to the GH distance, computing the Gromov–Wasserstein distance also requires solving a non-convex optimization problem. Recently, semidefinite relaxations of both the GH and Gromov–Wasserstein distances were studied in Villar et al. ( 2016 ). While allowing polynomial-time approximation, these relaxations admit distance 0 between non-isometric objects, losing the desired property of being a metric. Another result of potential interest from Villar et al. ( 2016 ) is a feasible algorithm for an upper bound of the GH (and therefore the mGH) distance. In Lipman and Daubechies ( 2011 ), the authors define the conformal Wasserstein distance, inspired by the Gromov–Wasserstein distance. It is a metric on the isometry classes of Riemannian 2-manifolds that can be accurately approximated in polynomial time under some reasonable conditions.

In Mémoli ( 2012 ), Mémoli introduces the modified Gromov–Hausdorff (mGH) distance, another relaxation of the GH distance that preserves the property of being a metric on the isometry classes of compact metric spaces. Same as the GH distance, the mGH distance is based on assignments between the metric spaces that are allowed to be non-injective. It turns out that the two distances are not equivalent in the general case (Oles and Vixie 2022 ), although they are topologically equivalent within precompact (in the GH-distance sense) families of compact metric spaces (Mémoli 2012 ).

Directly computing the mGH distance still poses an intractable combinatorial optimization of $O(N^N)$ time complexity (as compared to $O(N^{2N})$ for the standard GH distance). Our focus on the mGH distance in this paper is partially motivated by the so-called “structural theorem” (Theorem 5.1 in Mémoli ( 2012 )), which allows for the decomposition of the computation into solving a sequence of polynomial-time problems.

1.2 Shape-based graph matching

Because graphs are ubiquitous in applications, the task of graph matching, i.e. measuring how much a pair of graphs are different from each other, is extensively studied. Common approaches to exact graph matching are those based on graph shape, such as subgraph isomorphism and maximum common subgraph (Conte et al. 2004 ; Foggia et al. 2014 ). The shape-based approaches appear in many fields including neuroscience (Van Wijk et al. 2010 ), telecommunications (Shoubridge et al. 2002 ), and chemoinformatics (Raymond and Willett 2002 ; Vandewiele et al. 2012 ). While efficient heuristics for these approaches exist for special cases (e.g. planar graphs), applying them in the general case requires solving an NP-complete problem (Bunke 1997 ; Conte et al. 2004 ).

Recently, the Gromov–Hausdorff framework for graph matching was explored both theoretically (Aflalo et al. 2015 ) and in applications, e.g. in the fields of neuroscience (Lee et al. 2011 , 2006 ; Hendrikson 2016 ), social sciences, and finance (Hendrikson 2016 ). Undirected graphs admit metric space representation using the geodesic (shortest path length) distances on their vertex sets. However, the high computational cost of computing the isometry-invariant distances impedes a more widespread application of this approach.

1.3 Our contribution

Our main contribution is a theoretical framework for producing polynomial-time lower bounds of the GH and mGH distances. Furthermore, we present an algorithm for estimating the mGH distance, built upon this framework. We implement the algorithm for metric representations of unweighted graphs, leveraging their properties to reduce the polynomial order in the algorithm’s time complexity. We demonstrate the performance of the algorithm on several datasets of real-world and synthesized graphs of up to several thousand vertices.

The rest of the paper is structured as follows. Section 2 briefly reviews (Mémoli 2013 ) to formally define the GH and mGH distances, show their relation to each other, and state some of their properties. In Sects. 3 and 4 we discuss the ideas for establishing lower and upper bounds, respectively, of the mGH distance between finite metric spaces. In Sect. 5 , we describe the algorithm for estimating the mGH distance, show that it has polynomial time complexity, then discuss and present its implementation for the case of unweighted graphs. Computational examples from real-world and synthetic datasets are given in Sects. 6 and 7 summarizes our work. The Appendix contains pseudocode for the procedures and algorithms, omitted from the main paper for brevity.

2 Background

When talking about metric space given by set X and distance function $d_X: X \times X \rightarrow \mathbb {R}$ , we use notation $(X, d_X)$ and its shorter version X interchangeably. We expect the distinction between a set X and a metric space X to be clear from the context.

2.1 Definition of the Gromov–Hausdorff distance

Given $(X, d_X), (Y, d_Y) \in \mathcal {M}$ , where $\mathcal {M}$ denotes the set of all compact metric spaces, the GH distance measures how far the two metric spaces are from being isometric. It considers any “sufficiently rich” third metric space $(Z, d_Z)$ that contains isometric copies of X and Y , measuring the Hausdorff distance (in Z ) between these copies, and minimizes over the choice of the isometric copies and Z . Formally, the GH distance is defined as

where $\phi _X : X \rightarrow Z$ and $\phi _Y : Y \rightarrow Z$ are isometric embeddings of X and Y into Z , and $d_{\mathcal {H}}^Z$ is the Hausdorff distance in Z :

(see Fig. 1 ). Gromov has shown in Gromov ( 2007 ) that $d_{\mathcal{G}\mathcal{H}}$ is a metric on the isometry classes of $\mathcal {M}$ , constituting what is called a Gromov–Hausdorff space.

Illustration of the idea underlying the Gromov–Hausdorff distance

Although the above definition gives the conceptual understanding of the GH distance, it is not very helpful from the computational standpoint. The next subsection introduces a more practical characterization of the GH distance.

2.2 Characterization of the GH distance

For two sets X and Y , we say that relation $R \subseteq X \times Y$ is a correspondence if for every $x \in X$ there exists some $y \in Y$ s.t. $(x, y) \in R$ and for every $y \in Y$ there exists some $x \in X$ s.t. $(x, y) \in R$ . We denote the set of all correspondences between X and Y by $\mathcal {R}(X, Y)$ .

If R is a relation between metric spaces $(X, d_X)$ and $(Y, d_Y)$ , its distortion is defined as the number

Notice that any mapping $\varphi : X \rightarrow Y$ induces the relation $R_\varphi \buildrel \textrm{def}\over =\big \{\big (x, \varphi (x)\big ): x \in X \big \}$ , and we denote

Similarly, any $\psi : Y \rightarrow X$ induces the relation $R_\psi \buildrel \textrm{def}\over =\big \{\big (\psi (y), y\big ): y \in Y \big \}$ . If both $\varphi : X \rightarrow Y$ and $\psi : Y \rightarrow X$ are given, we can define the relation $R_{\varphi , \psi } \buildrel \textrm{def}\over =R_\varphi \cup R_\psi $ , and realize that it is actually a correspondence, $R_{\varphi , \psi } \in \mathcal {R}(X, Y)$ .

A useful result in Kalton and Ostrovskii ( 1999 ) identifies computing GH distance with solving an optimization problem, either over the correspondences between X and Y or over the functions $\varphi : X \rightarrow Y$ and $\psi : Y \rightarrow X$ :

By definition, distortion of any relation $R \subseteq X \times Y$ is bounded by ${{\,\textrm{dis}\,}}R \le d_{\max }$ , where $d_{\max } \buildrel \textrm{def}\over =\max \{{{\,\textrm{diam}\,}}X, {{\,\textrm{diam}\,}}Y\}$ . Combined with the characterization of the GH distance, it yields $d_{\mathcal{G}\mathcal{H}}(X, Y) \le \frac{1}{2} d_{\max }$ .

Let $*$ denote the (compact) metric space that is comprised of exactly one point. For any correspondence $R \in \mathcal {R}(X, *)$ , ${{\,\textrm{dis}\,}}R = \sup _{x, x' \in X} \big |d_X(x, x') - 0\big | = {{\,\textrm{diam}\,}}X$ . The above characterization implies that $d_{\mathcal{G}\mathcal{H}}(X, *) = \frac{1}{2}{{\,\textrm{diam}\,}}X$ , and, by an analogous argument, $d_{\mathcal{G}\mathcal{H}}(Y, *) = \frac{1}{2}{{\,\textrm{diam}\,}}Y$ . From the triangle inequality for the GH distance, $d_{\mathcal{G}\mathcal{H}}(X, Y) \ge \big |d_{\mathcal{G}\mathcal{H}}(X, *) - d_{\mathcal{G}\mathcal{H}}(Y, *)\big | = \frac{1}{2}|{{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y|$ .

2.3 Modifying the GH distance

Recall that for some $\varphi : X \rightarrow Y$ and $\psi : Y \rightarrow X$ , correspondence $R_{\varphi , \psi }$ is defined as $R_{\varphi , \psi } = R_\varphi \cup R_\psi $ . For any two elements in $R_{\varphi , \psi }$ , either both belong to $R_\varphi $ , or both belong to $R_\psi $ , or one of them belongs to $R_\varphi $ while the other belongs to $R_\psi $ . It follows that

where $C_{\varphi , \psi } \buildrel \textrm{def}\over =\displaystyle \sup _{x \in X, y \in Y} \big |d_X\big (x, \psi (y)\big ) - d_Y\big (\varphi (x), y\big )\big |$ .

Notice that the number $C_{\varphi , \psi }$ acts as a coupling term between the choices of $\varphi $ and $\psi $ in the optimization problem

making its search space to be of the size $|X|^{|Y|}|Y|^{|X|}$ . Discarding the coupling term $C_{\varphi , \psi }$ yields the notion of the modified Gromov–Hausdorff distance

Computing ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ requires solving two decoupled optimization problems whose search spaces are of the size $|X|^{|Y|}$ and $|Y|^{|X|}$ , respectively. An equivalent definition emphasizing this fact is given by

Similarly to $d_{\mathcal{G}\mathcal{H}}$ , ${\widehat{d}}_{\mathcal{G}\mathcal{H}}$ is a metric on the isometry classes of $\mathcal {M}$ . Moreover, ${\widehat{d}}_{\mathcal{G}\mathcal{H}}$ is topologically equivalent to $d_{\mathcal{G}\mathcal{H}}$ within GH-precompact families of metric spaces (Mémoli 2012 ).

2.4 Curvature sets and the structural theorem

Let $X \in \mathcal {M}$ , and consider $(x_1, \ldots , x_n) \in X^{\times n}$ , an n -tuple of points in X for some $n \in \mathbb {N}$ . The $n \times n$ matrix containing their pairwise distances is called the distance sample induced by $(x_1, \ldots , x_n)$ , and denoted by $D^{(x_1, \ldots , x_n)} \buildrel \textrm{def}\over =\big (d_X(x_i, x_j)\big )_{i,j=1}^n$ . A distance sample generalizes the notion of distance matrix of $\{x_1, \ldots , x_n\}$ when $x_1, \ldots , x_n$ are not necessarily distinct. Unlike a distance matrix, a distance sample may contain zeros off the main diagonal.

The n - th curvature set of X is then defined as a set of all $n \times n$ distance samples of X , denoted

For example, $\mathcal {K}_2(X)$ contains the same information as the entries of $D^X$ , the distance matrix of X ; when X is a smooth planar curve, then its curvature at every point can be calculated from the information contained in $\mathcal {K}_3(X)$ (Calabi et al. 1998 ), thus providing motivation for the name curvature sets .

Curvature sets contain information about the shape of a compact metric space in permutation-invariant way. In particular, any $X \in \mathcal {M}$ and $Y \in \mathcal {M}$ are isometric if and only if $\mathcal {K}_n(X) = \mathcal {K}_n(Y)$ for every $n \in \mathbb {N}$ (3.27 in Gromov ( 2007 )). To discriminate the shapes of X and Y , it is therefore reasonable to measure the difference between $\mathcal {K}_n(X)$ and $\mathcal {K}_n(Y)$ for various $n \in \mathbb {N}$ . Since both n -th curvature sets are subsets of the same space $\mathbb {R}^{n \times n}$ , Hausdorff distance is a natural metric between them. We equip the set of $n \times n$ matrices with distance $d_{l^\infty }(A, B) \buildrel \textrm{def}\over =\max _{i,j} \left| A_{i,j}-B_{i,j}\right| $ , and define

where $d_{\mathcal {H}}^{\mathbb {R}^{n \times n}}$ is the $d_{l^\infty }$ -induced Hausdorff distance on $\mathbb {R}^{n \times n}$ .

The choice of distance $d_{l^\infty }: \mathbb {R}^{n \times n} \times \mathbb {R}^{n \times n} \rightarrow \mathbb {R}$ complies with the notion of distortion of a mapping. If $\varphi $ is a mapping from X to Y for $X = \{x_1, \ldots , x_{|X|}\}$ , Y —metric spaces, then

The fact that $\varphi $ can be non-injective provides intuition for the possibility of identical points in a tuple from the definition of a distance sample.

An important result, extensively relied upon in this paper, is the so-called “structural theorem” for the mGH (Mémoli 2012 , 2013 ):

Notice that the bounds of the GH distance from the inequalities $\frac{1}{2} |{{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y| \le d_{\mathcal{G}\mathcal{H}}(X, Y) \le \frac{1}{2}d_{\max }$ also hold for the mGH distance:

while ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \le d_{\mathcal{G}\mathcal{H}}(X, Y) \le d_{\max }$ trivially follows from the definition of the mGH distance.

3 Lower bound for ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$

This section provides theoretical results and algorithms for an informative lower bound for the mGH distance between a pair of metric spaces X and Y . This and the following sections assume that the metric spaces are non-empty and finite, i.e. $1 \le |X|, |Y| < \infty $ . When talking about algorithmic time complexities, we denote the input size with $N \buildrel \textrm{def}\over =\max \{|X|, |Y|\}$ .

We notice that efficient estimation of either the GH or the mGH distance between finite metric spaces allows for its estimation between infinite compact metric spaces with desired accuracy. This is because for any $X \in \mathcal {M}$ and $\epsilon > 0$ , there exist finite $X_\epsilon \subset X$ that is an $\epsilon $ -net of X , which gives

Similarly, for any $Y \in \mathcal {M}$ there exists its finite $\epsilon $ -net $Y_\epsilon $ , and therefore

Feasible algorithms for lower bounds are important in e.g. classification tasks, where knowledge that a distance exceeds some threshold can make computing the actual distance unnecessary. In particular, if the mGH distance between metric representations of two graphs is $> 0$ , it immediately follows that the graphs are not isomorphic.

3.1 d -bounded matrices

Let A be a square matrix. We say that A is d - bounded for some $d \in \mathbb {R}$ if every off-diagonal entry of A is $\ge d$ . Similarly, A is positive-bounded if its off-diagonal entries are positive. Naturally, any d -bounded matrix for $d > 0$ is also positive-bounded.

Notice that a distance sample $D^{(x_1, \ldots , x_n)}$ of X is d -bounded if and only if $d_X(x_i, x_j) \ge d \quad \forall i \ne j$ , and positive-bounded if and only if $x_1, \ldots , x_n$ are distinct. By non-negativity of a metric, any distance sample is 0-bounded.

Let A and B be square matrices of the same size. If A is d -bounded for some $d > 0$ , and B is 0-bounded but not positive-bounded, then $d_{l^\infty }(A, B) \ge d$ .

Recall that a matrix B is a permutation similarity of a (same-sized) matrix A if $B = PAP^{-1}$ for some permutation matrix P . Equivalently, B is obtained from A by permuting both its rows and its columns according to some permutation $\pi $ : $B_{i,j} = A_{\pi (i),\pi (j)}$ . Given $n \in \mathbb {N}$ , we will denote the set of permutation similarities of $n \times n$ principal submatrices of A by $\textrm{PSPS}_n(A)$ .

A distance sample $K \in \mathcal {K}_n(X)$ is positive-bounded if and only if it is a permutation similarity of a principal submatrix of $D^X$ , i.e. if and only if $K \in \textrm{PSPS}_n(D^X)$ . In particular, there are no positive-bounded distance samples in $\mathcal {K}_n(X)$ if $n > |X|$ .

Let $K \in \mathcal {K}_n(X)$ be d -bounded for some $d > 0$ . If $n > |Y|$ , then ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ .

Notice that $L \in \mathcal {K}_n(Y)$ implies that L is 0-bounded (by non-negativity of a metric) and not positive-bounded (from Claim 2 ). Then

$\square $

For the standard GH distance, its lower bound implied by Theorem 1 is a direct consequence of its relationship with the n -packing number established in Cho ( 1997 ).

3.2 Obtaining d -bounded distance samples of large size

In order to apply Theorem 1 for some $d > 0$ , one needs to verify the existence of a d -bounded distance sample from X that exceeds Y in size. Ideally, one wants to know M ( X , d ), the largest size of a d -bounded distance sample of X :

Equivalently, M ( X , d ) is the so-called d -packing number of X : the largest number of points one can sample from X such that they all are at least d away from each other. Finding M ( X , d ) is equivalent to finding the size of a maximum independent set of the graph $G = \big (X, \{(x_i, x_j): d_X(x_i, x_j) < d\}\big )$ . Unfortunately, this problem is known to be NP-hard (Kégl 2002 ), and we therefore require approximation techniques to search for a sufficiently large d -bounded distance sample of X .

We implement greedy algorithm FindLarge K (see Appendix A for the pseudocode) that, given the distance matrix of X and some $d > 0$ , finds in $O(N^3)$ time a d -bounded distance sample $K \in \mathcal {K}_{{\widetilde{M}}(X, d)}(X)$ , where ${\widetilde{M}}(X, d)$ is an approximation of M ( X , d ). Informally, the algorithm iteratively removes rows (and same-index columns) from $D^X$ until all off-diagonal entries of the resulting K are $\ge d$ . At each step, the algorithm chooses to remove a row that is least d -bounded , i.e. one with the highest (non-zero) count of off-diagonal entries $< d$ .

Removing a row from K also “collaterally” removes an entry $< d$ from some of the remaining rows (due to removal of the corresponding column), potentially turning them into d -bounded. The counts of off-diagonal entries $<d$ in these rows define the number of newly appeared d -bounded rows in the remaining matrix at each step, thus controlling the duration of FindLarge K . In particular, the maximum duration (and therefore the worst approximation ${\widetilde{M}}(X, d)$ ) is attained when “collaterally” removed entries $< d$ reside in the least d -bounded rows at each step, which minimizes the number of d -bounded rows obtained from the removal. Let w be the maximum count of off-diagonal entries $<d$ in the rows of $D^X$ . Assuming the worst case scenario, each iteration of $\textsc {FindLarge}K(D^X, d)$ reduces the number of rows with w off-diagonal entries $<d$ by $w+1$ (one row is removed and the counts for w others become $w-1$ ), or to zero if fewer than $w+1$ of them remains. For the sake of simplicity, we will assume that $w+1$ divides | X |. It follows that after $\frac{|X|}{w+1}$ iterations the maximum count of off-diagonal entries $<d$ in the $\frac{w}{w+1}|X|$ rows of K is at most $w-1$ . More generally, if for some $k \le w$ the current K is comprised by $\big (1-\frac{k}{w+1}\big )|X|$ rows with at most $w-k$ off-diagonal entries $<d$ each, then after another

iterations the maximum count will be at most $w-k-1$ . By induction, K will contain no off-diagonal entries $<d$ after at most $w\frac{|X|}{w+1}$ iterations, which implies that its resulting size ${\widetilde{M}}(X, d)$ must be at least $\frac{1}{w+1}|X|$ . Because $M(X, d) \le |X|$ , the approximation ratio of ${\widetilde{M}}(X, d)$ is $\frac{1}{w+1}$ .

Notice that the obtained K does not need to be unique, because at any step there can be multiple least d -bounded rows. Choosing which one of them to remove allows selecting for some desired characteristics in the retained rows of K . In particular, Sect. 3.4 provides motivation to select for bigger entries in the resulting d -bounded distance sample K . To accommodate this, we choose to remove at each step a least d -bounded row with the smallest sum of off-diagonal entries $\ge d$ , so-called smallest least d -bounded row. Since uniqueness of a smallest least d -bounded row is not guaranteed either, we implemented procedure FindLeastBoundedRow (see Appendix B for the pseudocode) to find the index of the first such row in a matrix.

3.3 Using permutation similarities of principal submatrices of $D^Y$

Theorem 1 establishes that ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ from the existence of some d -bounded distance sample of sufficiently large size. However, such distance samples may not exist in certain cases (e.g. when $|X| = |Y|$ ), thus deeming Theorem 1 inapplicable. The main result of this subsection, Theorem 2 , complements Theorem 1 by allowing to verify ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ in those cases.

Let $K \in \mathcal {K}_n(X)$ be d -bounded for some $d > 0$ , and let $n \le |Y|$ . If for some $i \in \langle n \rangle \buildrel \textrm{def}\over =\{1, \ldots , n\}$

then $d_{l^\infty }\big (K, \mathcal {K}_n(Y)\big ) \ge d$ .

Let $L \in \mathcal {K}_n(Y)$ . If L is not positive-bounded, $d_{l^\infty }(K, L) \ge d$ follows from Claim 1 and the fact that any distance sample is 0-bounded. If L is positive-bounded, then $L \in \textrm{PSPS}_n(D^Y)$ from Claim 2 , and the premise entails

Because $d_{l^\infty }(K, L) \ge d$ for an arbitrary choice of $L \in \mathcal {K}_n(Y)$ , we have $d_{l^\infty }\big (K, \mathcal {K}_n(Y)\big ) \ge d.$ $\square $

A naive approach to proving $d_{l^\infty }(K, \mathcal {K}_n(Y)) \ge d$ is to show that $d_{l^\infty }(K, L) \ge d$ for each $L \in \mathcal {K}_n(Y)$ , which comprises an instance of the NP-hard QBAP. Instead, the premise of Lemma 1 (for a particular i ) can be checked by solving at most | Y | optimization problems of O (| Y |) time complexity each, as will be shown in the next subsection.

Let $K \in \mathcal {K}_n(X)$ be d -bounded for some $d > 0$ , and let $n \le |Y|$ . If for some $i \in \langle n \rangle $

then ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ .

3.4 Verifying ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$

Let $d > 0$ . To see if we can verify ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ from $D^X$ and $D^Y$ , we start by calling FindLarge K to obtain a d -bounded distance sample $K \in \mathcal {K}_n(X)$ for some $n \ge \frac{1}{w+1}M(X, d)$ . If $n > |Y|$ , then ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ follows immediately from Theorem 1 . Otherwise, we want to obtain this lower bound from Theorem 2 , which requires showing that some $i \in \langle n \rangle $ satisfies

Let i be fixed. If $L \in \textrm{PSPS}_n(D^Y)$ , then all entries in $\textrm{row}_{i}(L)$ come from one row of $D^Y$ , with $L_{i,i} = 0$ being the diagonal element in that row. The choice of i thus induces a (disjoint) partition of $\textrm{PSPS}_n(D^Y)$ :

where $\textrm{PSPS}_n^{i \leftarrow j}(D^Y)$ is the set of all permutation similarities of principal submatrices of $D^Y$ whose i -th row is comprised of the entries in $\textrm{row}_{j}(D^Y)$ . Therefore, the condition

can be verified by showing that

Let j , in addition to i , be fixed. Notice that any $L \in \textrm{PSPS}_n^{i\leftarrow j}(D^Y)$ corresponds to an injective mapping $f_L:\langle n \rangle \rightarrow \langle |Y| \rangle $ that defines the entries from $\textrm{row}_{j}(D^Y)$ that populate $\textrm{row}_{i}(L)$ : $L_{i, k} = D^Y_{j, f_L(k)}$ . In particular, $f_L(i) = j$ , because $L_{i,i} = D^Y_{j,j}$ for any $L \in \textrm{PSPS}_n^{i\leftarrow j}(D^Y)$ . Therefore, the condition

is equivalent to the non-existence of an injective $f_L:\langle n \rangle \rightarrow \langle |Y| \rangle $ such that $|K_{i, k} - D^Y_{j, f_L(k)}| < d \quad \forall k \in \langle n \rangle $ and $f_L(i) = j$ . The decision about the existence of a feasible assignment $f_L$ between the entries of $\textrm{row}_{i}(K)$ and $\textrm{row}_{j}(D^Y)$ is an instance of linear assignment feasibility problem. If such $f_L$ exists, it can be constructed by iteratively pairing the smallest unassigned $K_{i, k}$ to the smallest available $D^Y_{j, h}$ s.t. $|K_{i, k} - D^Y_{j, h}| < d$ , that is, by setting $f_L(k) = h$ (see Claim 3 ). It follows that each entry in $\textrm{row}_{j}(D^Y)$ needs to be checked at most once, and hence solving the feasibility problem takes O (| Y |) time if the entries in both $\textrm{row}_{i}(K)$ and $\textrm{row}_{j}(D^Y)$ are sorted. Procedure SolveFeasibleAssignment (see Appendix C for the pseudocode) implements the solution for a pair of vectors, given their entries are arranged in ascending order. We notice that ignoring the actual order of the (off-diagonal) entries in $\textrm{row}_{i}(K)$ and $\textrm{row}_{j}(D^Y)$ reflects the fact that curvature sets are closed under permutations of the underlying tuples of points.

Let $\textbf{v} \in \mathbb {R}^p, \textbf{u} \in \mathbb {R}^q$ be s.t. $v_1 \le \ldots \le v_p, u_1 \le \ldots \le u_q$ . If $\textsc {SolveFeasibleAssignment}(\textbf{v}, \textbf{u}, d)=\textrm{FALSE}$ , then no injective $f: \langle p \rangle \rightarrow \langle q \rangle $ s.t. $|v_t - u_{f(t)}| < d \quad \forall t \in \langle p \rangle $ exists.

Let t be the largest index for which $u_t$ could be feasibly assigned to some available entry of $\textbf{v}$ by $\textsc {SolveFeasibleAssignment}(\textbf{v}, \textbf{u}, d)$ . If such t does not exist, then $|v_1 - u_l| \ge d \quad \forall l \in \langle q \rangle $ and trivially no feasible assignment between $\textbf{v}$ and $\textbf{u}$ can exist.

Denote the partially constructed assignment by $f: \langle t \rangle \rightarrow \langle q \rangle $ , and notice that it is monotone by construction. In particular, every $u_l$ for $l > f(t)$ must remain available for assignments. Moreover, because $v_{t+1}$ could not be feasibly assigned to any entry of $\textbf{u}$ after $u_{f(t)}$ , which means that $v_t \le u_l - d \quad \forall l > f(t-1)$ .

Let $r \le t$ be the smallest index such that $f(r), f(r+1), \ldots , f(t)$ are a contiguous block, i.e. that $f(r) = f(t) - (t - r + 1)$ . Because $u_{f(r)-1}$ remains available (or does not exist due to $f(r)=1$ ), $v_r$ could not be feasibly assigned to any entry of $\textbf{u}$ before $u_{f(r)}$ , which means that $v_r \ge u_l + d \quad \forall l < f(r)$ .

Because $v_r \le \ldots \le v_t \le v_{t+1}$ , none of these $t-r+2$ entries can be feasibly assigned to the entries of $\textbf{u}$ before $u_{f(r)}$ or after $u_{f(t)}$ , meaning that they only have $t-r+1$ feasible matches in $\textbf{u}$ . By the pigeonhole principle, no feasible assignment between the two vectors can exist. $\square $

Intuitively, either sufficiently small or sufficiently large entries in $\textrm{row}_{i}(K)$ for some $i \in \langle n \rangle $ can render a feasible assignment $f_L$ impossible for every $j \in \langle |Y| \rangle $ , yielding $\Vert \textrm{row}_{i}(K) - \textrm{row}_{i}(L)\Vert _\infty \ge d \quad \forall L \in \textrm{PSPS}_n(D^Y)$ and therefore ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ from Theorem 2 . This provides the motivation behind considering the magnitude of the $\ge d$ entries when choosing a row to remove at each step of FindLarge K . Recall that such row is chosen by the auxiliary procedure FindLeastBoundedRow , that selects for bigger entries in the resulting K . The approach allows for a tighter lower bound in the case when the entries in $D^X$ are, generally speaking, bigger than those in $D^Y$ . The converse case is covered by similarly obtaining and handling a d -bounded distance sample of Y .

Calling SolveFeasibleAssignment $(\textrm{row}_{i}(K), \textrm{row}_{j}(D^Y), d)$ for every $j \in \langle |Y| \rangle $ is sufficient to check whether a particular i satisfies $\Vert \textrm{row}_{i}(K) - \textrm{row}_{i}(L)\Vert _\infty \ge d \quad \forall L \in \textrm{PSPS}_n(D^Y)$ . Procedure CheckTheoremB (see Appendix D for the pseudocode) makes such check for each $i \in \langle n \rangle $ to decide whether ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ follows from Theorem 2 for the d -bounded K . The procedure sorts the entries in the rows of K and $D^Y$ prior to the checks, which takes $O(N\log N)$ time for each of the O ( N ) rows. This allows solving each of the $O(N^2)$ feasibility problems in O ( N ) time, making the time complexity of CheckTheoremB $O(N^2\log N + N^3) = O(N^3)$ .

Notice that both Theorem 1 and 2 regard a largest-size d -bounded distance sample of only one metric space, X . However, its counterpart for Y is equally likely to provide information for discriminating the two metric spaces. Making use of the symmetry of ${\widehat{d}}_{\mathcal{G}\mathcal{H}}$ , we summarize theoretical findings of this section under $O(N^3)$ -time procedure VerifyLowerBound (see Appendix E for the pseudocode), that attempts to prove ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ .

3.5 Obtaining the lower bound

Procedure VerifyLowerBound is a decision algorithm that gives a “yes” or “no” answer to the question if a particular value can be proven to bound ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ from below. In order to obtain an informative lower bound, one wants to find the largest value for which the answer is “yes”. Since ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \le \frac{1}{2}d_{\max }$ , the answer must be “no” for any value above $\frac{1}{2}d_{\max }$ , and therefore it suffices to limit the scope to $(0, \frac{1}{2}d_{\max }]$ . To avoid redundancy when checking the values from this interval, we consider the following result.

Let $\Delta $ denote the set of absolute differences between the distances in X and Y ,

and let $\{\delta _i\}_{i=1}^{|\Delta |}$ represent the sorting order of $\Delta $ , $0 = \delta _1< \ldots < \delta _{|\Delta |} = d_{\max }$ . If $\delta _i< d_1 < d_2 \le \delta _{i+1}$ for some $d_1, d_2$ and $i \in \langle |\Delta |-1 \rangle $ , then $\textsc {VerifyLowerBound}(D^X, D^Y, d_1) = \textsc {VerifyLowerBound}(D^X, D^Y, d_2)$ .

VerifyLowerBound considers the value of its argument d only through comparisons of the form “ $\delta < d$ ” for some $\delta $ , that occur in FindLarge K and SolveFeasibleAssignment . Notice that the values of $\delta $ compared with d in FindLarge K are the entries of $D^X$ or $D^Y$ , and therefore belong to $\Delta $ as

The values of $\delta $ compared with d in SolveFeasibleAssignment belong to $\Delta $ by construction.

For any $\delta \in \Delta $ , $\delta < d_1$ if and only if $\delta < d_2$ . This is because $\delta < d_2$ implies $\delta < d_1$ from $\delta \notin [d_1, d_2)$ , while $\delta < d_1$ implies $\delta < d_2$ trivially. It follows that both FindLarge K and SolveFeasibleAssignment yield identical outputs on $d_1$ and $d_2$ (and otherwise identical inputs), and hence so does VerifyLowerBound . $\square $

Claim 4 implies that the largest $\delta \in \Delta $ s.t. $\textsc {VerifyLowerBound}(D^X, D^Y, \delta ) = \textrm{TRUE}$ is the largest $d \in \mathbb {R}$ s.t. $\textsc {VerifyLowerBound}(D^X, D^Y, d) = \textrm{TRUE}$ . We use this fact to implement the procedure FindLowerBound (see Appendix F for the pseudocode), that obtains a lower bound of ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ by calling $\textsc {VerifyLowerBound}(D^X, D^Y, \delta )$ for each $\delta \in \Delta $ from largest to smallest, and stops once the output is TRUE. Since $|\Delta | = O(N^4)$ in the general case, the time complexity of FindLowerBound is $O(N^7)$ .

Using binary search on $\Delta $ instead of traversing its values in descending order reduces the number of calls to VerifyLowerBound from $O(N^4)$ to $O(\log N)$ , bringing the time complexity of FindLowerBound to $O(N^3 \log N)$ . We however notice that, given some $d_1 < d_2$ , $\textsc {VerifyLowerBound}(D^X, D^Y, d_2) = \textrm{TRUE}$ does not guarantee $\textsc {VerifyLowerBound}(D^X, D^Y, d_1) = \textrm{TRUE}$ due to the heuristic nature of FindLarge K (for example, it is possible to obtain ${\widetilde{M}}(X, d_1) \le |Y| < {\widetilde{M}}(X, d_2)$ even though, trivially, $M(X, d_1) \ge M(X, d_2) \ge {\widetilde{M}}(X, d_2)$ ). It follows that relying on the binary search in FindLowerBound can result in failing to find the largest $\delta \in \Delta $ s.t. $\textsc {VerifyLowerBound}(D^X, D^Y, \delta ) = \textrm{TRUE}$ , and thus in reducing time complexity at the cost of potentially lower accuracy.

An increase in accuracy at the expense of time complexity can be achieved by modifying $\textsc {FindLowerBound}(D^X, D^Y)$ and its subroutines so that Theorem 2 for the d -bounded distance samples tries to prove not only ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d}{2}$ but also ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{d^*}{2}$ for some $d^* < d$ , $d^* \in \Delta $ . For every pair $i \in \langle n \rangle , j \in \langle |Y| \rangle $ , the modified $\textsc {CheckTheoremB}(K, D^Y, d)$ finds the largest $d^* \le d$ s.t. $\textsc {SolveFeasibleAssignment}(\textrm{row}_{i}(K), \textrm{row}_{j}(D^Y), d^*)=\textrm{TRUE}$ (instead of checking the existence of feasible assignment for d only) and returns the largest $d^*$ s.t. some i satisfies $\Vert \textrm{row}_{i}(K) - \textrm{row}_{i}(L)\Vert _\infty \ge d^* \quad \forall L \in \textrm{PSPS}_n(D^Y)$ . Accordingly, VerifyLowerBound propagates this value of $d^*$ to FindLowerBound , which stores their maximum from the already processed part of $\Delta $ (and proceeds only if this maximum is smaller than the current $\delta _i$ ). Because the existence of feasible assignment for $d^*$ is monotonic in $d^*$ , using binary search on $\Delta $ is sufficient to find the largest $d^* \le d$ s.t. $\textsc {SolveFeasibleAssignment}(\textrm{row}_{i}(K), \textrm{row}_{j}(D^Y), d^*)=\textrm{TRUE}$ . It follows that the increase in time complexity of the modified CheckTheoremB (and therefore FindLowerBound ) is only by a factor of $O(\log N)$ .

The modification would be able to provide better bounds by additionally trying smaller distance samples with larger entries in Theorem 2 . In particular, it is guaranteed to prove the baseline lower bound ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \ge \frac{1}{2}|{{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y|$ . Assuming without loss of generality ${{\,\textrm{diam}\,}}X \ge {{\,\textrm{diam}\,}}Y$ , the call to $\textsc {FindLarge}$ K $(D^X, {{\,\textrm{diam}\,}}X)$ from $\textsc {VerifyLowerBound}(D^X, D^Y, {{\,\textrm{diam}\,}}X)$ will yield K with non-zero entries that each are at least $({{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y)$ away from all $D^Y$ entries. Because the $({{\,\textrm{diam}\,}}X)$ -bounded K is also $({{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y)$ -bounded, the modified $\textsc {CheckTheoremB}(K, D^Y, {{\,\textrm{diam}\,}}X)$ will output $d^* \ge {{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y$ , ensuring that the resulting lower bound is at least $\frac{1}{2}|{{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y|$ .

This is in contrast with the original FindLowerBound , in which the only easy guarantee for proving the baseline lower bound via Theorem 2 is the presence of ${{\,\textrm{diam}\,}}X$ values in K produced by $\textsc {FindLarge}K(D^X, {{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y)$ . However, because $\textsc {FindLarge}K$ prioritizes the number of entries $\ge {{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y$ in a row of $D^X$ over their magnitude, and because a point with a distance ${{\,\textrm{diam}\,}}X$ can have arbitrarily many distances $< {{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y$ , establishing practical conditions for the output of FindLowerBound to be $\ge \frac{1}{2}({{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y)$ is non-trivial.

4 Upper bound for ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$

4.1 construction method.

To obtain an upper bound of ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ , we recall the definition

where $\varphi $ and $\psi $ are the mappings $\varphi :X \rightarrow Y$ and $\psi :Y \rightarrow X$ and the infimums are taken over the corresponding function spaces. It follows that ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y) \le \frac{1}{2}\max \{{{\,\textrm{dis}\,}}\varphi , {{\,\textrm{dis}\,}}\psi \}$ for any particular choice of $\varphi $ and $\psi $ . Considering the exponential size of function spaces, we rely on a small randomized sample of mappings to tighten the upper bound. To sample $\varphi :X \rightarrow Y$ , we use the construction method, a heuristic for solving quadratic assignment problems (Gilmore 1962 ; Burkard et al. 1998 ). The construction method iteratively maps each $x \in X$ to some $y \in Y$ , chosen by a greedy algorithm to minimize ${{\,\textrm{dis}\,}}\varphi $ as described below.

Let $X = \{x_1, \ldots , x_{|X|}\}$ and $Y = \{y_1, \ldots , y_{|Y|}\}$ . We randomly choose a permutation $\pi $ of $\langle |X| \rangle $ to represent the order in which the points in X are mapped. At step i we map $x_{\pi (i)}$ by choosing $y_{j_i}$ and setting $\varphi (x_{\pi (i)}) \buildrel \textrm{def}\over =y_{j_i}$ . We represent these choices by inductive construction $R_\varphi ^{(i)} = R_\varphi ^{(i-1)} \cup \{(x_{\pi (i)}, y_{j_i})\}$ for $i = 1, \ldots , |X|$ , where $R_\varphi ^{(0)} \buildrel \textrm{def}\over =\emptyset $ . The particular choice of $y_{j_i}$ at step i is made to minimize distortion of resultant $R_\varphi ^{(i)}$ :

After carrying out all | X | steps, $\varphi :X \rightarrow Y$ is given by the constructed relation $R_\varphi \buildrel \textrm{def}\over =R_\varphi ^{(|X|)}$ , and by definition, ${{\,\textrm{dis}\,}}\varphi = {{\,\textrm{dis}\,}}R_\varphi $ .

Notice the possible ambiguity in the choice of $y_{j_i}$ when $y \in Y$ minimizing ${{\,\textrm{dis}\,}}\Big (R_\varphi ^{(i-1)} \cup \big \{(x_{\pi (i)}, y)\big \}\Big )$ is not unique. In particular, any $y \in Y$ can be chosen as $y_{j_1}$ at step 1, since ${{\,\textrm{dis}\,}}\big \{(x_{\pi (i)}, y_{j_1})\big \} = 0$ is invariant to the said choice. In the case of such ambiguity, our implementation simply decides to map $x_{\pi (i)}$ to $y_{j_i}$ of the smallest index $j_i$ . However, in applications one might want to modify this logic to leverage the knowledge of the relationship between the points from two metric spaces.

We formalize the above heuristic under a randomized, $O(N^3)$ -time procedure SampleSmallDistortion (see Appendix G for the pseudocode) that samples a mapping between the two metric spaces with the intent of minimizing its distortion, and outputs this distortion. We then describe an algorithm FindUpperBound (see Appendix H for the pseudocode), that repeatedly calls SampleSmallDistortion to find $\varphi ^*:X \rightarrow Y$ and $\psi ^*:Y \rightarrow X$ , the mappings of the smallest distortion among those sampled from $X \rightarrow Y$ and $Y \rightarrow X$ , respectively, and finds an upper bound for ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ as $\frac{1}{2}\max \{{{\,\textrm{dis}\,}}\varphi ^*, {{\,\textrm{dis}\,}}\psi ^*\}$ . The time complexity of FindUpperBound is therefore $O(sN^3)$ , where s is the total number of sampled mappings.

4.2 Approximation ratio bounds

Unlike the lower bound estimation, our heuristic for the upper bound operates within the solution space of ${\widehat{d}}_{\mathcal{G}\mathcal{H}}$ formulation as a combinatorial minimization problem. This allows leveraging a result for bottleneck assignment problems bounding the ratio between the two extrema of the objective function (see e.g. Theorem 2 in Burkard and Fincke ( 1985 )) to understand better the convergence of SampleSmallDistortion . Indeed, solving $\inf _{\phi :X\rightarrow Y} {{\,\textrm{dis}\,}}\phi $ can be cast as a variant of the QBAP with the cost function $c(i, j, k, h) \buildrel \textrm{def}\over =|D^X_{i,j} - D^Y_{k,h}|$ that allows non-injective assignments and hence has the search space of size $|Y|^{|X|}$ . Assuming $|X| > 1$ , the maximum of its objective function ${{\,\textrm{dis}\,}}\phi $ on the feasible region is $d_{\max }$ . We consider a scaled but otherwise identical minimization problem with the cost function ${\widetilde{c}}(i, j, k, h) \buildrel \textrm{def}\over =\frac{|D^X_{i,j} - D^Y_{k,h}|}{d_{\max }} \in [0, 1]$ , whose objective function has the minimum of $\frac{\inf _{\phi :X\rightarrow Y} {{\,\textrm{dis}\,}}\phi }{d_{\max }}$ . The result by Burkard and Fincke ( 1985 ) treats the values of ${\widetilde{c}}$ as identically distributed random variables, and states that if | X | and | Y | satisfy

for some $\epsilon , q \in [0, 1]$ , then the approximation ratio of the solution by the maximum is probabilistically bounded by

Let b be the smallest distortion discovered by SampleSmallDistortion after a number of tries, and consider some $r \ge 1$ . If for $\epsilon \buildrel \textrm{def}\over =\frac{rd_{\max }}{b}-1$ we can find q that satisfies both ( ⋆ ) and $q > \frac{\log |Y|}{|X|}$ , the above result allows us to bound the probability that the approximation ratio of b is worse than r :

An analogous probabilistic bound applies to the minimization of distortion of $\psi :Y \rightarrow X$ . These bounds can be used to adaptively control the sample size s in FindUpperBound for achieving some target accuracy with the desired level of confidence.

5 Algorithm for estimating ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$

The algorithm for estimating the mGH distance between compact metric spaces X and Y (“the algorithm”) consists of the calls $\textsc {FindLowerBound}(D^X, D^Y)$ and $\textsc {FindUpperBound}(D^X, D^Y)$ . Notice that ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ is found exactly whenever the outputs of the two procedures match. Time complexity of the algorithm is $O(N^7)$ whenever s , the number of mappings sampled from $X \rightarrow Y$ and $Y \rightarrow X$ in FindUpperBound , is limited by $O(N^4)$ .

To obtain a more practical result, we now consider a special case of metric spaces induced by unweighted undirected graphs. We show that estimating the mGH distance between such metric spaces in many applications has time complexity $O(N^3 \log N)$ , and present our implementation of the algorithm in Python.

5.1 ${\widehat{d}}_{\mathcal{G}\mathcal{H}}$ between unweighted undirected graphs

Let $G = (V_G, E_G)$ be a finite undirected graph. For every pair of vertices $v, v' \in V_G$ , we define $d_G(v, v')$ as the shortest path length between v to $v'$ . If weights of the edges in $E_G$ are positive, the resulting function $d_G : V_G \times V_G \rightarrow [0, \infty ]$ is a metric on $V_G$ . We say that the metric space $(V_G, d_G)$ is induced by graph G , and notice that its size $|V_G|$ is the order of G . By convention, the shortest path length between vertices from different connected components of a graph is defined as $\infty $ , and therefore $(V_G, d_G)$ is compact if and only if graph G is connected.

For brevity, we will use notation $G \buildrel \textrm{def}\over =(V_G, d_G)$ , assuming that the distinction between graph G and metric space G induced by this graph is clear from the context. In particular, we refer to the mGH distance between compact metric spaces induced by undirected connected graphs G and H as ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(G, H)$ , or even call it “the mGH distance between graphs G and H ”.

Let G , H be connected unweighted undirected graphs. Notice that ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(G, H) = 0$ if and only if graphs G and H are isomorphic. We use the following result to reduce the computational cost of estimating ${\widehat{d}}_{\mathcal{G}\mathcal{H}}(G, H)$ as compared to that in the general case.

If G is a finite connected unweighted undirected graph, all entries in distance matrix $D^G$ of the corresponding compact metric space are from $\{0, 1, \ldots , {{\,\textrm{diam}\,}}G\}$ .

Claim 5 implies that there are at most $d_{\max } + 1$ distinct entries in any distance sample of either G or H , where $d_{\max } \buildrel \textrm{def}\over =\max \{{{\,\textrm{diam}\,}}G, {{\,\textrm{diam}\,}}H\}$ . Recall that SolveFeasibleAssignment traverses the two sorted vectors strictly left to right, in each vector keeping track only of its part after the last assigned entry. It follows that both vectors can be represented simply as counts of entries $0, 1, \ldots , d_{\max }$ they contain, with traversing a vector corresponding to decrementing the leftmost non-zero count. In particular, assigning an entry in one vector to an entry in another is then equivalent to decrementing the corresponding counts in each of the vectors, which reflects the injectivity of the assignment being constructed. Notice that if $v_i$ is assigned to $u_j$ at some step and the remaining entries of the two vectors contain $v_i$ and $u_j$ , respectively, SolveFeasibleAssignment will make an identical assignment at the next step. It follows that representing the vectors by counting their identical entries allows the procedure to make bulk assignments, which reduces the time complexity of SolveFeasibleAssignment from O ( N ) to $O(d_{\max })$ and makes the complexity of CheckTheoremB $O(N^2 d_{\max })$ , where $N \buildrel \textrm{def}\over =\max \{|V_G|, |V_H|\}$ .

From the perspective of optimization theory, representing vectors as counts of their entries reformulates the linear assignment feasibility problem of SolveFeasibleAssignment as a transportation feasibility problem.

Another implication of Claim 5 narrows the set of absolute differences between the distances in G and H to $\Delta = \{0, 1, \ldots , d_{\max }\}$ , reducing the time complexity of traversing its elements from $O(N^4)$ to $O(d_{\max })$ . This bounds the time complexity of FindLowerBound by $O(N^3 d_{\max })$ . The complexity of the entire algorithm is therefore $O(N^3 d_{\max })$ when the number of sampled mappings is $s = O(d_{\max })$ .

Network diameter often scales logarithmically with network size, e.g. in Erdős–Rényi random graph model (Albert and Barabási 2002 ) and Watts–Strogatz small-world model (Watts and Strogatz 1998 ), or even sublogarithmically, e.g. in the configuration model with i.i.d. degrees (van der Hofstad et al. 2007 ) and Barabási–Albert preferential attachment model (Cohen and Havlin 2003 ). This suggests the time complexity of the algorithm in applications to be $O(N^3 \log N)$ , deeming it practical for shape comparison for graphs of up to a moderate order.

5.2 Implementation

We have implemented the algorithm for estimating mGH between unweighted graphs in Python 3.7 as part of | scikit-tda| package (Saul and Tralie 2019 ) ( https://github.com/scikit-tda ). Our implementation takes adjacency matrices (optionally in sparse format) of unweighted undirected graphs as inputs. If an adjacency matrix corresponds to a disconnected graph, the algorithm approximates it with its largest connected component. The number of mappings to sample from $X \rightarrow Y$ and $Y \rightarrow X$ in FindUpperBound is parametrized as a function of | X | and | Y |.

6 Computational examples

This section demonstrates the performance of the algorithm on some real-world and synthetic networks. The real-world networks were sourced from the Enron email corpus (Klimt and Yang 2004 ), the cybersecurity dataset collected at Los Alamos National Laboratory (Kent 2016 ), and the functional magnetic resonance imaging dataset ABIDE I (Di Martino et al. 2014 ).

6.1 Methodology and tools

Given a pair of connected graphs, we approximate the mGH distance between them by ${\tilde{d}} \buildrel \textrm{def}\over =\frac{b_L + b_U}{2}$ , where $b_L$ and $b_U$ are the lower and upper bounds produced by the algorithm. The relative error of the algorithm is estimated by

noting that the case of $b_U = 0$ implies that the algorithm has found the mGH distance of 0 exactly. In addition, we compute the utility coefficient defined by

where $b'_L \le b_L$ is the baseline lower bound: $b'_L \buildrel \textrm{def}\over =\frac{1}{2}|{{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y| \le {\widehat{d}}_{\mathcal{G}\mathcal{H}}(X, Y)$ for $X, Y \in \mathcal {M}$ . The utility coefficient thus quantifies the tightening of the lower bound achieved by using Theorems 1 and 2 .

Due to the possible suboptimality of the mappings selected by using the construction method (see Sect. 4 ), the upper bound may not be computed accurately enough. From the definition of relative error $\eta $ and utility coefficient $\upsilon $ , a sufficiently loose upper bound can make $\eta $ arbitrarily close to 1 and $\upsilon $ —arbitrarily small.

We measured $\eta $ and $\upsilon $ separately for each dataset. For the real-world data, we also used the approximated distances ${\tilde{d}}$ to identify graphs of outlying shapes and matched these graphs to events or features of importance in application domains, following the approach taken in e.g. (Bunke and Kraetzl 2004 ; Bunke et al. 2006 ; Koutra et al. 2013 ; Pincombe 2005 ). Unlike (Bunke and Kraetzl 2004 ; Koutra et al. 2013 ), and Pincombe ( 2005 ) that focus on local time outliers (under the assumption of similarity between graphs from consecutive time steps), we considered the outliers with respect to the entire time range (where applicable), similarly to Bunke et al. ( 2006 ).

To identify the outliers, we applied the Local Outlier Probability (LoOP) method (Kriegel et al. 2009 ) to the graphs using their approximated pairwise mGH distances. LoOP uses a local space approach to outlier detection and is robust with respect to the choice of parameters (Kriegel et al. 2009 ). The score assigned by LoOP to a data object is interpreted as the probability of the object to be an outlier. We binarize the score into outlier/non-outlier classification using the commonly accepted confidence levels of 95%, 99%, and 99.9% as thresholds, chosen empirically for each individual dataset. We used the implementation of LoOP in Python (Constantinou 2018 ) (version 0.2.1), modified by us to allow non-Euclidean distances between the objects. We ran LoOP with locality and significance parameters set to $k = 20$ and $\lambda = 1$ , respectively.

The synthetic graphs were generated according to Erdős–Rényi, Watts–Strogatz, and Barabási–Albert network models. We used implementations of the models provided in Hagberg et al. ( 2008 ) (version 2.1).

All computations were performed on a single 2.70GHz core of Intel i7-7500U CPU.

6.2 Enron email corpus

Enron email corpus (available at https://www.cs.cmu.edu/~./enron/ ) represents a collection of email conversations between the employees, mostly senior management, of the Enron corporation from October 1998 to March 2002. We used the latest version of the dataset from May 7, 2015, which contains roughly 500K emails from 150 employees.

Associating employees with graph vertices, we view the dataset as a dynamic network whose 174 instances reflect weekly corporate email exchange over the course of 3.5 years. An (unweighted) edge connecting a pair of vertices in a network instance means a mutual exchange of at least one email between the two employees on a particular week. The time resolution of 1 week was suggested in Sulo et al. ( 2010 ) for providing an appropriate balance between noise reduction and information loss in Enron dataset.

We expected major events related to the Enron scandal in the end of 2001 to cause abnormal patterns of weekly email exchange between the senior management, distorting the shape of the corresponding network instances. As a consequence, metric spaces generated by such network instances would be anomalously far from the rest with respect to the mGH distance.

Outlier probabilities assigned to the weekly email exchange networks. Red indicates outlier probabilities $> 0.99$ , corresponding to the weeks of Sep 17, Oct 29, Nov 5, and Nov 26 in the year 2001

In preparation for the analysis, we discarded all empty network instances corresponding to the weeks of no email exchange between the employees (of which all 28 weeks happened before May 1999). Each of the remaining 146 graphs was then replaced with its largest connected component. The distribution of the order of the resulting graphs had a mean of 68.2, a standard deviation of 99.8, and a maximum of 706.

We estimated the mGH distances in all 10,585 distinct pairs of the non-empty connected network instances. Average graph order and computing time per one pair were distributed as $68.2 \pm 70.3$ and $0.93\textrm{s} \pm 3.91\textrm{s}$ , respectively (where $\mu \pm \sigma $ refers to distribution with a mean of $\mu $ and a standard deviation of $\sigma $ ; no assumptions of normality are made, and we use standard deviation solely as a measure of spread). The algorithm found exact mGH distances in 74.4% of the graph pairs, with relative error $\eta $ and utility coefficient $\upsilon $ distributed as $0.057 \pm 0.118$ and $0.043 \pm 0.085$ , respectively. The ratio between the means of $\upsilon $ and $\eta $ (i.e. $\frac{\upsilon }{\eta } + 1 = \frac{\upsilon + \eta }{\eta } = \frac{b_U - b_{L'}}{b_L - b_{L'}}$ ) implies that using Theorems 1 and 2 on average reduced the relative error by a factor of 1.75.

We ran LoOP on the network instances using their (approximated) pairwise mGH distances ${\tilde{d}}$ . The resulting outlier probability assigned to each network instance (Fig. 2 ) thus measures the abnormality of its shape.

To see if the abnormal shape of email exchange corresponds to events of high importance from the Enron timeline, we applied the threshold of 0.99 to the outlier probabilities. Three out of four network instances that scored above the threshold correspond to the weeks of known important events in 2001, namely the weeks of Oct 29, Nov 5, and Nov 26 (each date is a Monday). As the closing stock price of Enron hit an all-time low on Friday, Oct 26, Enron’s chairman and CEO Kenneth Lay was making multiple calls for help to Treasure Secretary Paul O’Neill and Commerce Secretary Donald Evans on Oct 28–29. Enron fired both its treasurer and in-house attorney on Nov 5, admitted to overstating its profits for the last five years by $600M on Nov 8, and agreed to be acquired by Dynegy Inc. for $9B on Nov 9. On Nov 28, Dynegy Inc. aborted the plan to buy Enron, and on Dec 2, Enron went bankrupt.

We conclude that the abnormal shape of email exchange networks tends to correspond to disturbances in their environment, and that the algorithm estimates the mGH distance accurately enough to capture it.

6.3 LANL cybersecurity dataset

Los Alamos National Laboratory (LANL) cybersecurity dataset (available at https://csr.lanl.gov/data/cyber1/ ) represents 58 consecutive days of event data collected from LANL’s corporate computer network (Kent 2016 ). For our purposes, we considered its part containing records of authentication events, generated by roughly 11K users on 18K computers, and collected from individual Windows-based desktops and servers. During the 58-day data collection period, a “red team” penetration testing operation had taken place. As a consequence, a small subset of authentications were labeled as red team compromise events, presenting well-defined bad behavior that differed from normal user and computer activity. The labeling is not guaranteed to be exhaustive, and authentication events corresponding to red team actions, but not labeled as such, are likely to be present in the data. Heard and Rubin-Delanchy ( 2016 )

Each authentication event occurs between a pair of source and destination computers. Viewing the computers as graph vertices, we associated each user with a dynamic network, whose instances reflect their daily authentication activity within the 58-day period. An (unweighted) edge connecting a pair of vertices in a network instance means that at least one authentication event by the user has occurred between the two computers on a particular day. The user-based approach to graph representation of the data aims to capture the patterns of user account misuse that are expected to occur during a cyberattack.

Our objective was to develop an unsupervised approach that can identify the red team activity associated with a user’s account. We expected that frequent compromise events within the course of one day should distort the shape of the corresponding network instance. As a consequence, metric spaces generated by such network instances would be anomalously far from the rest.

For the analysis, we selected 20 users with the highest total of associated red team events and randomly chose another 20 users from those unaffected by the red team activity (see Fig. 3 ). Each of their 40 dynamic networks initially comprised of 58 instances. We discarded all empty network instances corresponding to the days of inactivity of a user account, and replaced each of the remaining 1,997 graphs with its largest connected component. The distribution of the order in the resulting graphs had a mean of 32.7 and a standard deviation of 75.8. The largest graphs were associated with the red team-affected user U1653@DOM1—their order was distributed with a mean of 178.2, a standard deviation of 391.5, and a maximum of 2,343.

Frequency of red team events in daily authentication activity of the selected users. Grey indicates days of no authentication activity by user. Dashed line separates the two groups of 20 users

Separately for each of the selected users, we estimated the mGH distances in all distinct pairs of the non-empty connected network instances associated with her account. Table 1 shows average graph order in a pair and the performance metrics of the algorithm, aggregated per user subsets. We notice that using Theorems 1 and 2 has reduced the relative error by a factor of 3.5 on average. In addition, the algorithm did not seem to perform worse on the larger graphs associated with user U1653@DOM1.

Outlier probability assigned to user-based daily authentication graphs. Red indicates outlier probabilities $> 0.999$ . Grey indicates empty graphs (excluded from analysis). The dashed line separates the two groups of 20 users

Separately for each user, we ran LoOP on the associated network instances using their (approximated) pairwise mGH distances ${\tilde{d}}$ . The resulting outlier probability assigned to each network instance (Fig. 4 ) thus measures the abnormality of its shape for the particular user.

To see if the days of high compromise activity can be identified from the abnormal shape of the corresponding network instances, we approached the identification as a binary classification task. User’s daily activity is considered a compromise if it includes at least 30 red team events, and is predicted as such if the outlier probability assigned to the corresponding network instance is $>0.999$ . The resulting confusion matrix of our shape-based binary classifier is shown in Table 2 , establishing its accuracy, precision, and recall as 99.5%, 18.2%, and 100%, respectively.

Even though recall is prioritized over precision when identifying intrusions, low precision can be impractical when using the classifier alone. However, high recall suggests that combining the shape-based classifier with another method can improve performance of the latter. For example, classifying daily activity as a compromise if and only if both methods agree on it is likely to increase the other method’s precision without sacrificing its recall.

We conclude that sufficiently frequent compromise behavior tends to distort the shape of networks representing user authentication activity, and that the algorithm estimates the mGH distance accurately enough to pick up the distortion. However, regular operations can cause similar distortion, and the shape of user authentication alone may be insufficient to accurately identify compromise behavior.

6.4 ABIDE I dataset

The Autism Brain Imaging Data Exchange I (ABIDE I, https://fcon_1000.projects.nitrc.org/indi/abide/abide_I.html) (Di Martino et al. 2014 ) is a resting state functional magnetic resonance imaging dataset, collected to improve understanding of the neural bases of autism. Besides the diagnostic group (autism or healthy control), the information collected from the study subjects also includes their sex, age, handedness category, IQ, and current medication status. We considered the preprocessed version of ABIDE I used in Kazeminejad and Sotero ( 2019 ), containing brain networks of 816 subjects, including 374 individuals with autism spectrum disorder and 442 healthy controls.

Brain network of an individual is comprised of 116 nodes, each corresponding to a region of interest (ROI) in the automatic anatomical labeling atlas of the brain (Tzourio-Mazoyer et al. 2002 ). Connectivity of the network represents correlations between the brain activity in the ROI pairs, with the brain activity extracted as a time series for each region. Namely, an (unweighted) edge connects two nodes if Spearman’s rank correlation coefficient between the corresponding pair of time series is in the highest 20% of all such coefficients for distinct ROI pairs. This approach of thresholding connectivity to obtain an unweighted graph representation is commonly used for functional brain networks (Achard and Bullmore 2007 ; Supekar et al. 2008 ; Redcay et al. 2013 ; Rudie et al. 2013 ; Rubinov and Sporns 2010 ).

Outlier probability assigned to brain networks of study subjects. Blue indicates outlier probabilities $> 0.95$ , and red—outlier probabilities $> 0.999$ . The latter correspond to the subjects MaxMun_c_0051332, MaxMun_b_0051323, and MaxMun_c_0051335. The remaining outlier probabilities are 0

We replaced the brain network of each subject with its largest component, which did not introduce a significant change to the data: the distribution of the order in the resulting 816 graphs had a mean of about 116.0 and a standard deviation of 0.1.

We estimated the mGH distances in all 332,520 distinct pairs of the connected brain networks. Average graph order and computing time per one pair were distributed as $116.0 \pm 0.1$ and $0.40\textrm{s} \pm 20.29\textrm{s}$ , respectively. The algorithm found exact mGH distances in 78.6% of the graph pairs, with relative error $\eta $ and utility coefficient $\upsilon $ distributed as $0.072 \pm 0.139$ and $0.361 \pm 0.214$ , respectively. We notice that using Theorems 1 and 2 has reduced the relative error by a factor of 5 on average.

We ran LoOP on the brain networks using their (approximated) pairwise mGH distances ${\tilde{d}}$ . The resulting outlier probability assigned to each brain network (Fig. 5 ) thus measures the abnormality of its shape.

To see if abnormal shape of a brain network corresponds to certain features of the individual, we applied the thresholds of 0.999 and 0.95 to the outlier probabilities. We were unable to identify the corresponding brain network shapes with outlying values of the available measurements, neither for the 3 subjects who scored above the threshold of 0.999 nor for the 54 subjects who scored above 0.95.

To see if the brain networks of subjects within the same diagnostic group tend to have similar shape, we performed cluster analysis based on the mGH distances ${\tilde{d}}$ . We used | scipy| implementation of hierarchical agglomerative clustering algorithm to split the 816 networks into two clusters (by the number of diagnostic groups in the dataset). The smaller cluster was comprised of the same 3 subjects who scored above the outlier probability threshold of 0.999. Discarding them as outliers and rerunning the analysis resulted in two clusters of 51 and 762 subjects, respectively. The clusters did not show any correspondence with the diagnostic groups, thus providing no evidence that the within-group mGH distances are smaller than the inter-group ones. However, we notice a significant overlap between the 54 subjects with an outlier probability above 0.95 and the cluster of 51 individuals, with 47 people shared between the two groups. This implies that the abnormal brain networks tend to be closer to one another than to the “regular” brain networks. This observation suggests that abnormality of the brain network shape is influenced by currently unknown features which are not included in the dataset.

We conclude that the algorithm estimates the mGH distance between Spearman’s correlation-based functional brain networks with high accuracy. However, detected shape abnormalities do not seem to correspond to a conclusive pattern related to autism spectrum disorder identification.

6.5 Synthetic networks

To test performance of the algorithm on synthetic networks, we generated 100 graphs per each of Erdős–Rényi (random), Watts–Strogatz (small-world), and Barabási–Albert (scale-free) network models. The order n of each graph was selected uniformly at random between 10 and 200, and other parameters of the model were based on n . In the Erdős–Rényi G ( n , p ) model, the probability p for an edge between a vertex pair to appear was selected uniformly at random between $\frac{0.5\log n}{n}$ and $\frac{1.5\log n}{n}$ . In the Watts–Strogatz G ( n , 2 k , p ) model, k , half of the average vertex degree, was selected uniformly at random between 1 and $\lfloor 0.5 \log ^2 n \rceil $ , and the probability p for an edge to get rewired was selected uniformly at random between $\frac{0.5\log n}{n}$ and $\frac{1.5\log n}{n}$ . In the Barabási–Albert G ( n , m ) model, the number of edges m to attach from a new node to the existing nodes was selected uniformly at random between 1 and $\lfloor \log ^2 n \rceil $ .

After generating the graphs, we replaced each of them with its largest connected component. For each set, we estimated the mGH distances in all distinct pairs of the 100 connected graphs therein. Table 3 shows the average graph order in a pair and the performance metrics of the algorithm, aggregated per individual data sets.

We notice that the algorithm performs significantly worse on the Erdős–Rényi graphs. One possible explanation is that there are fewer identically connected vertices in random graphs than in those resembling real-world networks, which contributes to the combinatorial complexity of the search for distortion-minimizing mappings to obtain the upper bound. Recall from Sect. 6.1 that inaccurate computations of the upper bound alone can have a detrimental effect on both $\eta $ and $\upsilon $ .

Another interesting observation is that Theorems 1 and 2 have smaller utility when applied to the Watts–Strogatz graphs. Recall that a Watts–Strogatz small-world graph is generated from a lattice ring with each node connected to its 2 k neighbors ( k for each side), by randomly rewiring a fraction (roughly, p ) of its edges. For a small p , the rewired edges serve as shortcuts between the otherwise remote vertices and have a highly nonlinear effect on the diameter (Watts and Strogatz 1998 ). This allows for high variability in the diameters of generated graphs, thus contributing to the tightness of the baseline lower bounds $b'_L \buildrel \textrm{def}\over =\frac{1}{2}|{{\,\textrm{diam}\,}}X - {{\,\textrm{diam}\,}}Y|$ .

We conclude that the algorithm performs better on graphs with scale-free and small-world properties, observed in many real-world networks.

7 Conclusion

The main contribution of this work is a feasible method for finding a lower bound for the mGH (and therefore GH) distance between finite metric spaces. The approach, based on the introduced notion of d -bounded distance samples, yields a polynomial-time algorithm for estimating the mGH distance. The algorithm is implemented as part of Python | scikit-tda| library for the case of compact metric spaces induced by unweighted graphs. It is also shown that in the case of unweighted graphs of order N whose diameter scales at most logarithmically with N the algorithm has time complexity $O(N^3 \log N)$ .

To test the algorithm’s performance, we applied it to both real and synthesized networks. Among the synthesized networks we tested, the best performance was observed for graphs with scale-free and small-world properties. We have also found that the algorithm performed well on the real-world email exchange, computer, and brain networks. The mGH distance was used to successfully detect outlying shapes corresponding to events of significance. This suggests that the proposed algorithm may be useful for graph shape matching in various application domains.

Abbreviations

Index set $\{1, \ldots , n\}$ , for $n \in \mathbb {N}$

The ceiling of $a \in \mathbb {R}$

The nearest integer to $a \in \mathbb {R}$

$l_\infty $ -norm of vector $\textbf{v} = \begin{bmatrix}v_1&v_2&\ldots&\end{bmatrix}$

i -th row of matrix A : $\begin{bmatrix}A_{i,1}&A_{i,2}&\ldots&\end{bmatrix}$

Matrix obtained from matrix A by removing its i -th row and j -th column

$l_\infty $ -induced matrix distance: $\max _{i,j} \left| A_{i,j} - B_{i,j}\right| $

Number of elements in set S

Cartesian product $\underbrace{S \times \ldots \times S}_{n \text { times}}$ , for $n \in \mathbb {N}$

Set of the mappings of S into T

The Hausdorff distance between the subsets S , T of metric space $(X, d_X)$ : $\displaystyle d_{\mathcal {H}}^X(S, T) \buildrel \textrm{def}\over =\max \left\{ \sup _{s \in S} \inf _{t \in T} d_X(s, t), \; \sup _{t \in T} \inf _{s \in S} d_X(s, t) \right\} $

Distance matrix of metric space $(X, d_X)$ , where $X = \{x_1, \ldots , x_{|X|}\}$ : $D^X_{i,j} \buildrel \textrm{def}\over =d_X(x_i, x_j) \quad \forall i,j = 1, \ldots , |X|$

Set of compact metric spaces

Diameter of metric space $(X, d_X) \in \mathcal {M}$ : $\displaystyle \sup _{x, x' \in X} d_X(x, x')$

Achard S, Bullmore E (2007) Efficiency and cost of economical brain functional networks. PLoS Comput Biol 3(2):e17

Article Google Scholar

Aflalo Y, Bronstein A, Kimmel R (2015) On convex relaxation of graph isomorphism. Proc Natl Acad Sci 112(10):2942–2947

Article MathSciNet Google Scholar

Albert R, Barabási A-L (2002) Statistical mechanics of complex networks. Rev Mod Phys 74(1):47

Bunke H (1997) On a relation between graph edit distance and maximum common subgraph. Pattern Recogn Lett 18(8):689–694

Bunke H, Dickinson P, Humm A, Irniger C, Kraetzl M (2006) Computer network monitoring and abnormal event detection using graph matching and multidimensional scaling. In: Industrial conference on data mining. Springer, pp 576–590

Bunke H, Kraetzl M (2004) Classification and detection of abnormal events in time series of graphs. In: Data mining in time series databases. World Scientific, pp 127–148

Burkard RE, Cela E, Pardalos PM, Pitsoulis LS (1998) The quadratic assignment problem. In: Handbook of combinatorial optimization. Springer, pp 1713–1809

Burkard RE, Fincke U (1985) Probabilistic asymptotic properties of some combinatorial optimization problems. Discret Appl Math 12(1):21–29

Calabi E, Olver PJ, Shakiban C, Tannenbaum A, Haker S (1998) Differential and numerically invariant signature curves applied to object recognition. Int J Comput Vision 26(2):107–135

Chazal F, Cohen-Steiner D, Guibas LJ, Mémoli F, Oudot SY (2009) Gromov-Hausdorff stable signatures for shapes using persistence. In: Computer graphics forum, vol 28. Wiley Online Library, pp 1393–1403

Cho M-S (1997) On the optimal covering of equal metric balls in a sphere. Pure Appl Math 4(2):137–144

MathSciNet Google Scholar

Cohen R, Havlin S (2003) Scale-free networks are ultrasmall. Phys Rev Lett 90(5):058701

Constantinou V (2018) PyNomaly: anomaly detection using local outlier probabilities (loOP). J Open Source Softw 3(30):845

Conte D, Foggia P, Sansone C, Vento M (2004) Thirty years of graph matching in pattern recognition. Int J Pattern Recognit Artif Intell 18(03):265–298

Di Martino A, Yan C-G, Li Q, Denio E, Castellanos FX, Alaerts K, Anderson JS, Assaf M, Bookheimer SY, Dapretto M et al (2014) The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Mol Psychiatry 19(6):659–667

Foggia P, Percannella G, Vento M (2014) Graph matching and learning in pattern recognition in the last 10 years. Int J Pattern Recognit Artif Intell 28(01):1450001

Gilmore PC (1962) Optimal and suboptimal algorithms for the quadratic assignment problem. J Soc Ind Appl Math 10(2):305–313

Gromov M (2007) Metric structures for Riemannian and non-Riemannian spaces. Springer

Gromov M (1981) Groups of polynomial growth and expanding maps. Publications Mathématiques de l’Institut des Hautes Études Scientifiques 53(1):53–78

Hagberg A, Swart P, Chult Daniel S (2008) Exploring network structure, dynamics, and function using NetworkX. Technical report, Los Alamos National Lab.(LANL), Los Alamos, NM (United States)

Heard N, Rubin-Delanchy P (2016) Network-wide anomaly detection via the Dirichlet process. In: 2016 IEEE conference on intelligence and security informatics (ISI). IEEE, pp 220–224

Hendrikson R et al. (2016) Using Gromov-Wasserstein distance to explore sets of networks. University of Tartu, Master Thesis, 2

Kalton NJ, Ostrovskii MI (1999) Distances between Banach spaces

Kaustubh S, Vinod M, Daniel R, Mark M, Greicius Michael D (2008) Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Comput Biol 4(6):e1000100

Kazeminejad A, Sotero RC (2019) Topological properties of resting-state fMRI functional networks improve machine learning-based autism classification. Front Neurosci 12:1018

Kégl B (2002) Intrinsic dimension estimation using packing numbers. In: NIPS. Citeseer, pp 681–688

Kent AD (2016) Cyber security data sources for dynamic network research. In: Dynamic networks and cyber-security. World Scientific, pp 37–65

Klimt B, Yang Y (2004) The enron corpus: a new dataset for email classification research. In: European conference on machine learning. Springer, pp 217–226

Koutra D, Vogelstein JT, Faloutsos C (2013) Deltacon: a principled massive-graph similarity function. In: Proceedings of the 2013 SIAM international conference on data mining. SIAM, pp 162–170

Kriegel H-P, Kröger P, Schubert E, Zimek A (2009) LoOP: local outlier probabilities. In: Proceedings of the 18th ACM conference on information and knowledge management, pp 1649–1652

Lee H, Chung MK, Kang H, Kim B-N, Lee DS et al (2006) Persistent network homology from the perspective of dendrograms. IEEE Trans Med Imaging 12:2381–2381

Google Scholar

Lee H, Chung MK, Kang H, Kim B-N, Lee DS (2011) Computing the shape of brain networks using graph filtration and Gromov-Hausdorff metric. In: International conference on medical image computing and computer-assisted intervention. Springer, pp 302–309

Lipman Y, Daubechies I (2011) Conformal Wasserstein distances: comparing surfaces in polynomial time. Adv Math 227(3):1047–1077

Majhi S, Vitter J, Wenk C (2019) Approximating Gromov-Hausdorff distance in euclidean space. arXiv:1912.13008

Mémoli F (2007) On the use of Gromov-Hausdorff distances for shape comparison

Mémoli F (2009) Spectral Gromov-Wasserstein distances for shape matching. In: 2009 IEEE 12th international conference on computer vision workshops, ICCV Workshops. IEEE, pp 256–263

Mémoli F (2011) Gromov-Wasserstein distances and the metric approach to object matching. Found Comput Math 11(4):417–487

Mémoli F (2012) Some properties of Gromov-Hausdorff distances. Discrete Comput Geom 48(2):416–440

Mémoli F (2013) The Gromov-Hausdorff distance: a brief tutorial on some of its quantitative aspects. Actes des rencontres du CIRM 3(1):89–96

Mémoli F, Sapiro G (2004) Comparing point clouds. In: Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing, pp 32–40

Oles V, Vixie KR (2022) Lipschitz (non-)equivalence of the Gromov–Hausdorff distances, including on ultrametric spaces. arXiv:2204.10250

Pankaj KA, Kyle F, Abhinandan N, Anastasios S, Yusu W (2018) Computing the Gromov-Hausdorff distance for metric trees. ACM Trans Algorithms (TALG) 14(2):1–20

Peyré G, Cuturi M, Solomon J (2016) Gromov-Wasserstein averaging of kernel and distance matrices. In: International conference on machine learning. PMLR, pp 2664–2672

Pincombe B (2005) Anomaly detection in time series of graphs using arma processes. Asor Bull 24(4):2

Raymond JW, Willett P (2002) Maximum common subgraph isomorphism algorithms for the matching of chemical structures. J Comput Aided Mol Des 16(7):521–533

Redcay E, Moran JM, Mavros PL, Tager-Flusberg H, Gabrieli JDE, Whitfield-Gabrieli S (2013) Intrinsic functional network organization in high-functioning adolescents with autism spectrum disorder. Front Hum Neurosci 7:573

Rubinov M, Sporns O (2010) Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52(3):1059–1069

Rudie JD, Brown JA, Devi B-P, Hernandez LM, Dennis EL, Thompson PM, Bookheimer SY, Dapretto MJNC (2013) Altered functional and structural brain network organization in autism. NeuroImage Clin 2:79–94

Saul N, Tralie C (2019) Scikit-TDA: topological data analysis for python. https://doi.org/10.5281/zenodo.2533369

Schmiedl F (2017) Computational aspects of the Gromov-Hausdorff distance and its application in non-rigid shape matching. Discrete Comput Geom 57(4):854

Shoubridge P, Kraetzl M, Wallis WAL, Bunke H (2002) Detection of abnormal change in a time series of graphs. J Interconnection Netw 3(01n02):85–101

Sturm K-T (2006) On the geometry of metric measure spaces. Acta Math 196(1):65–131

Sulo R, Berger-Wolf T, Grossman R (2010) Meaningful selection of temporal resolution for dynamic networks. In: Proceedings of the eighth workshop on mining and learning with graphs, pp 127–136

Tuzhilin AA (2016) Who invented the Gromov-Hausdorff distance? arXiv:1612.00728

Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M (2002) Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15(1):273–289

van der Hofstad R, Hooghiemstra G, Znamenski D (2007) A phase transition for the diameter of the configuration model. Int Math 4(1):113–128

Van Wijk Bernadette CM, Stam Cornelis J, Andreas D (2010) Comparing brain networks of different size and connectivity density using graph theory. PloS one 5(10):e13701

Vandewiele NM, Van Geem KM, Reyniers M-F, Marin GB (2012) Kinetic model construction using chemo-informatics. Genesyst Chem Eng J 207:526–538

Villani C (2003) Topics in optimal transportation, vol 58. American Mathematical Soc

Villar S, Bandeira AS, Blumberg AJ, Ward R (2016) A polynomial-time relaxation of the Gromov-Hausdorff distance. arXiv:1610.05214

Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world’networks. Nature 393(6684):440–442

Download references

Acknowledgements

Part of this work was performed during the stay of Vladyslav Oles at Los Alamos National Laboratory, and he acknowledges the provided support. In addition, the authors would like to thank Facundo Mémoli for detailed clarification of his work and useful comments, Amirali Kazeminejad for sharing preprocessed ABIDE I dataset, Bob Week for insightful conversations, Iana Khotsianivska for helping with figure design, Grace Grimm for reviewing and editing, and Luigi Boschetti for encouragement and inspiration.

Author information

Authors and affiliations.

Oak Ridge National Laboratory, Oak Ridge, USA

Vladyslav Oles, Nathan Lemons & Alexander Panchenko

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vladyslav Oles .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A: Procedure FindLarge K

Appendix B: Procedure FindLeastBoundedRow

Appendix C: Procedure SolveFeasibleAssignment

Appendix D: Procedure CheckTheoremB

Appendix E: Procedure VerifyLowerBound

Appendix F: Procedure FindLowerBound

Appendix G: Procedure SampleSmallDistortion

Appendix H: Procedure FindUpperBound

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Oles, V., Lemons, N. & Panchenko, A. Efficient estimation of the modified Gromov–Hausdorff distance between unweighted graphs. J Comb Optim 48 , 14 (2024). https://doi.org/10.1007/s10878-024-01202-1

Download citation

Accepted : 04 June 2024

Published : 23 August 2024

DOI : https://doi.org/10.1007/s10878-024-01202-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Gromov–Hausdorff distance
Shape analysis
Network science
Anomaly detection
Find a journal
Publish with us
Track your research

Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
Advertising & Talent Reach devs & technologists worldwide about your product, service or employer brand
OverflowAI GenAI features for Teams
OverflowAPI Train & fine-tune LLMs
Labs The future of collective knowledge sharing
About the company Visit the blog

Collectives™ on Stack Overflow

Find centralized, trusted content and collaborate around the technologies you use most.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

Get early access and see previews of new features.

Assigning Values to an Array with for Loop Python

I'm trying to assign the values of a string to different array indexes

but I'm getting an error called "list assignment out of range"

I tried using

but it gave an error called "list index out of range"

made it work with no error but the outcome was wrong

because it keep concatenating the new assigned value with old values in the next index

How it should work:

returnedList[ '52:33:42:40:94:10:19, -60' , '22:34:42:24:89:70:89, -90' , '87:77:98:54:81:23:71, -81' ]

with each iteration it assign the first to char to uuidVal (ex: 52, 22, 87) and the last two char to distVal (ex: 60, 90, 81)

at the end uuidArray should have these values [52, 22, 87]

and distArray should have these values [60, 90, 81]

Note: using .append concatenate the values, for example if used with distArray like distArray.append(distVal) the values will be like this [60, 6090, 609081]

variable-assignment

@michaelpri Nope, they have values. – AMS91 Commented Jan 3, 2015 at 23:53

4 Answers 4

yes you will get error list index out of range for:

you are accessing the index that is not created yet

lets see this demo:

your code should be like this:

output will be uudiArray: ['52', '22', '87'] and distArray: ['60', '6090', '609081']

Thanks, now I understand why my approach is wrong. But what should I do instead to make it work? – AMS91 Commented Jan 3, 2015 at 23:56
The input data is a string containing two digits number. The output should be an array with each index containing a string of two digits numbers. The first loop is used to assign select the index, the second loop is to get a string from an array of string in each iteration. I cannot select indexes with a string value – AMS91 Commented Jan 4, 2015 at 0:28
can u update in ur post with sample input and expected output that will be more clear – Hackaholic Commented Jan 4, 2015 at 0:29
Thx it works now, I was commenting distVal = "" that why it was keeping to concatenate. – AMS91 Commented Jan 4, 2015 at 1:17

When you define distArray as: distArray = []

You are initializing a list with 0 elements, so distArray[2] will correctly throw an error, since you are attempting to access an element past the total length of the array.

There are two ways to deal with this:

Use append . This takes the list and extends it by the element contained in the function call. This is to be preferred for all but the rarest of occasions, imo.
Explicitly define an empty list. This can be done using something like: distArray = [0]*num_elements , where num_elements is the number of elements you want to have. This will create a list of size num_elements all equal to 0.

Using append will no give an error but the problem it will concatenate the new value with the old values. So if index[0]='81' and the next value is 79, index[1] will equal '8179' and so on. The second method it give wrong output, too long form the beginning. The first one starts great exactly like I wanted but the issue it keep concatenating – AMS91 Commented Jan 4, 2015 at 0:23

Others have already explained the mistake, so I'll just leave my 2c on how to work this out. First of all you can use pure Python:

I'm using None-type objects to allocate the array (whereas many people prefer zeros) because they can't be interpreted as an integer or bool.

If your process is going to be RAM-intensive, you should better use numpy arrays. And there is a highly efficient way to create an empty array in numpy.

Notice that you should manually select a data type.

What you are trying to achieve is basically a simplified hash-map/table. If you're not sure about the maximum value, you can consider writing your own 'dynamic' array, that will increase in size, if called outside its borders, instead of raising the error.

This thing will adapt to your needs.

Your Answer

Reminder: Answers generated by artificial intelligence tools are not allowed on Stack Overflow. Learn more

Sign up or log in

Post as a guest.

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged python arrays for-loop variable-assignment or ask your own question .

The Overflow Blog
Ryan Dahl explains why Deno had to evolve with version 2.0
From PHP to JavaScript to Kubernetes: how one backend engineer evolved over time
Featured on Meta
We've made changes to our Terms of Service & Privacy Policy - July 2024
Bringing clarity to status tag usage on meta sites
Feedback requested: How do you use tag hover descriptions for curating and do...
What does a new user need in a homepage experience on Stack Overflow?

Hot Network Questions

Everyone hates this Key Account Manager, but company won’t act
Can objective morality be derived as a corollary from the assumption of God's existence?
bash script quoting frustration
What does the Fizeau experiment now do?
Can the speed of light inhibit the synchronisation of a power grid?
DateTicksFormat -> Automatic different in 14.1 than in 14.0
Assumptions in a ideal circuit which consists of ideal wires(zero resistance)
Sticker on caption phone says that using the captions can be illegal. Why?
The McDonald's Option
Would it take less thrust overall to put an object into higher orbit?
Millennial reign and New Heaven and New Earth
How to determine if a set is countable or uncountable?
Jacobi two square's theorem last step to conclusion
What is the lesson of the Book of Iyov for the "average" person
Matrix with \guilsinglright, \guilsinglleft and \textlquill, \textrquill
Are there any virtues in virtue ethics that cannot be plausibly grounded in more fundamental utilitarian principles?
How would I make an agent noun out of the word "autodice -es f" or "autodicia"
Name of engineering civil construction device for flattening tarmac
Print tree of uninstalled dependencies and their filesizes for apt packages
What does 北渐 mean?
Short story in which the protagonist shrinks to the size of his model train set and is run over by one of his trains
Can you successfully substitute pickled onions for baby onions in Coq Au Vin?
Can figere come with a dative?
Can a "sharp turn" on a trace with an SMD resistor also present a risk of reflection?

IMAGES

Python for loop (10 easy examples with syntax)
Loops in Python
Python While Loop With Assignment [With 4 Real Examples]
Python For Loops Explained (Python for Data Science Basics #5)
Loops in Python with Examples
Python For Loops Explained (Python for Data Science Basics #5)

COMMENTS

Python Variable assignment in a for loop
6 I understand that in Python regular c++ style variable assignment is replaced by references to stuff ie
How to use Python While with Assignment[4 Examples]
This Python tutorial explains what is python while with assignment , the Python While loop conditions and how we can assign variables with different methods.
21 Python for Loop Exercises and Examples
To get a clear idea about how a for loop works, I have provided 21 examples of using for loop in Python. You can go through these examples and understand the working of for loops in different scenarios.
How To Use Assignment Expressions in Python
In this tutorial, you used assignment expressions to make compact sections of Python code that assign values to variables inside of if statements, while loops, and list comprehensions.
Python's Assignment Operator: Write Robust Assignments
In this tutorial, you'll learn how to use Python's assignment operators to write assignment statements that allow you to create, initialize, and update variables in your code.
PEP 572
Particularly with the while loop, this can remove the need to have an infinite loop, an assignment, and a condition. It also creates a smooth parallel between a loop which simply uses a function call as its condition, and one which uses that as its condition but also uses the actual value.
The Walrus Operator: Python's Assignment Expressions
In this tutorial, you'll learn about assignment expressions and the walrus operator. The biggest change back in Python 3.8 was the inclusion of the := operator, which you can use to assign variables in the middle of expressions. You'll see several examples of how to take advantage of this feature.
Python "for" Loops (Definite Iteration)
In this introductory tutorial, you'll learn all about how to perform definite iteration with Python for loops. You'll see how other programming languages implement definite iteration, learn about iterables and iterators, and tie it all together to learn about Python's for loop.
8 Python while Loop Examples for Beginners
Looking for a Python while loop example? Discover what a Python while loop is and how to use it efficiently.
Python for loop and if else Exercises [10 Exercise Programs]
This Python loop exercise include the following: - It contains 18 programs to solve using if-else statements and looping techniques. Solutions are provided for all questions and tested on Python 3. This exercise is nothing but an assignment to solve, where you can solve and practice different loop programs and challenges.
python
113 Since Python 3.8, code can use the so-called "walrus" operator ( := ), documented in PEP 572, for assignment expressions. This seems like a really substantial new feature, since it allows this form of assignment within comprehensions and lambda s. What exactly are the syntax, semantics, and grammar specifications of assignment expressions?
Python For Loops
Python For Loops. A for loop is used for iterating over a sequence (that is either a list, a tuple, a dictionary, a set, or a string). This is less like the for keyword in other programming languages, and works more like an iterator method as found in other object-orientated programming languages. With the for loop we can execute a set of ...
Python while Loop (With Examples)
In Python, we use the while loop to repeat a block of code until a certain condition is met.
Assignment Operators in Python
The Python Operators are used to perform operations on values and variables. These are the special symbols that carry out arithmetic, logical, and bitwise computations. The value the operator operates on is known as the Operand. Here, we will cover Different Assignment operators in Python.
Assignment Expressions: The Walrus Operator
In this lesson, you'll learn about the biggest change in Python 3.8: the introduction of assignment expressions. Assignment expression are written with a new notation (:=) .This operator is often called the walrus operator as it resembles the eyes and tusks of a walrus on its side.
18 Python while Loop Examples and Exercises
In Python programming, we use while loops to do a task a certain number of times repeatedly. The while loop checks a condition and executes…
4. More Control Flow Tools
4. More Control Flow Tools ¶ As well as the while statement just introduced, Python uses a few more that we will encounter in this chapter.
Assign values to array during loop
I am currently learning Python (I have a strong background in Matlab). I would like to write a loop in Python, where the size of the array increases with every iteration (i.e., I can assign a newly
Python Exercises, Practice, Challenges
Coding Exercises with solutions for Python developers. Practice 220+ Python Topic-specific exercises. Solve Python challenges, assignments, programs.
python
I want to make an assignment to an item of a list in a single line for loop. First i have a list, where each list items are dictionary object. Then, i do for loop over each item of the list and co...
Efficient estimation of the modified Gromov-Hausdorff ...
Because the existence of feasible assignment for $d^*$ is monotonic in \ ... We used the implementation of LoOP in Python (Constantinou 2018) (version 0.2.1), modified by us to allow non-Euclidean distances between the objects. We ran LoOP with locality and significance parameters set to $k = 20$ and $\lambda = 1$, respectively.
Assigning Values to an Array with for Loop Python
The input data is a string containing two digits number. The output should be an array with each index containing a string of two digits numbers. The first loop is used to assign select the index, the second loop is to get a string from an array of string in each iteration. I cannot select indexes with a string value - AMS91 Jan 4, 2015 at 0:28