null hypothesis testing process

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
Collect data in a way designed to test the hypothesis.
Perform an appropriate statistical test .
Decide whether to reject or fail to reject your null hypothesis.
Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

an estimate of the difference in average height between the two groups.
a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved August 26, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

Null Hypothesis: Definition, Rejecting & Examples

By Jim Frost 6 Comments

What is a Null Hypothesis?

The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

Photograph of Rodin's statue, The Thinker who is pondering the null hypothesis.

Null Hypothesis H 0 : No effect exists in the population.
Alternative Hypothesis H A : The effect exists in the population.

In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.

In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!

You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.

Related post : What is an Effect in Statistics?

Null Hypothesis Examples

Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.


Does the vaccine prevent infections?	The vaccine does not affect the infection rate.
Does the new additive increase product strength?	The additive does not affect mean product strength.
Does the exercise intervention increase bone mineral density?	The intervention does not affect bone mineral density.
As screen time increases, does test performance decrease?	There is no relationship between screen time and test performance.

After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.

Let’s see how you reject the null hypothesis and get to those more exciting findings!

When to Reject the Null Hypothesis

So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.

The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .

After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.

When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .

Rejecting the Null Hypothesis

Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!

When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .

Failing to Reject the Null Hypothesis

Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!

Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .

That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!

Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.

Related posts : How Hypothesis Tests Work and Interpreting P-values

How to Write a Null Hypothesis

The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.

Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics

Group Means

T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.

For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.

Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.

Group Proportions

Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.

For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.

Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .

Correlation and Regression Coefficients

Some studies assess the relationship between two continuous variables rather than differences between groups.

In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.

For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.

Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.

For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.

The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .

Related post : Understanding Correlation

Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.

Reader Interactions

January 11, 2024 at 2:57 pm

Thanks for the reply.

January 10, 2024 at 1:23 pm

Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?

January 10, 2024 at 2:15 pm

Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.

Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.

With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.

So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).

For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.

I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!

February 20, 2022 at 9:26 pm

Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”

February 23, 2022 at 9:21 pm

Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.

It’s the alternative hypothesis that typically contains does not equal.

There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.

In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.

February 15, 2022 at 9:32 am

Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent

Comments and Questions Cancel reply

13.1 Understanding Null Hypothesis Testing

Learning objectives.

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of adults with clinical depression, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.

You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.

“Null Hypothesis” retrieved from http://imgs.xkcd.com/comics/null_hypothesis.png (CC-BY-NC 2.5)

Role of Sample Size and Relationship Strength

Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”



Sample Size	Weak	Medium	Strong
Small ( = 20)	No	No	= Maybe = Yes
Medium ( = 50)	No	Yes	Yes
Large ( = 100)	= Yes = No	Yes	Yes
Extra large ( = 500)	Yes	Yes	Yes

Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

“Conditional Risk” retrieved from http://imgs.xkcd.com/comics/conditional_risk.png (CC-BY-NC 2.5)

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Share This Book

Increase Font Size

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 13: Inferential Statistics

Understanding Null Hypothesis Testing

Learning Objectives

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favour of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Table 13.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant
Sample Size	Weak relationship	Medium-strength relationship	Strong relationship
Small ( = 20)	No	No	= Maybe = Yes
Medium ( = 50)	No	Yes	Yes
Large ( = 100)	= Yes = No	Yes	Yes
Extra large ( = 500)	Yes	Yes	Yes

Statistical Significance Versus Practical Significance

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.

Long Descriptions

“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]

“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]

Media Attributions

Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Values in a population that correspond to variables measured in a study.

The random variability in a statistic from sample to sample.

A formal approach to deciding between two interpretations of a statistical relationship in a sample.

The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.

The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.

When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.

The probability that, if the null hypothesis were true, the result found in the sample would occur.

How low the p value must be before the sample result is considered unlikely in null hypothesis testing.

When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.

Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List

PMC5635437.1 ; 2015 Aug 25
PMC5635437.2 ; 2016 Jul 13
➤ PMC5635437.3; 2016 Oct 10

Null hypothesis significance testing: a short tutorial

Cyril pernet.

1 Centre for Clinical Brain Sciences (CCBS), Neuroimaging Sciences, The University of Edinburgh, Edinburgh, UK

Version Changes

Revised. amendments from version 2.

This v3 includes minor changes that reflect the 3rd reviewers' comments - in particular the theoretical vs. practical difference between Fisher and Neyman-Pearson. Additional information and reference is also included regarding the interpretation of p-value for low powered studies.

Peer Review Summary

Review date	Reviewer name(s)	Version reviewed	Review status
	Dorothy Vera Margaret Bishop		Approved with Reservations
	Stephen J. Senn		Approved
	Stephen J. Senn		Approved with Reservations
	Marcel ALM van Assen		Not Approved
	Daniel Lakens		Not Approved

Although thoroughly criticized, null hypothesis significance testing (NHST) remains the statistical method of choice used to provide evidence for an effect, in biological, biomedical and social sciences. In this short tutorial, I first summarize the concepts behind the method, distinguishing test of significance (Fisher) and test of acceptance (Newman-Pearson) and point to common interpretation errors regarding the p-value. I then present the related concepts of confidence intervals and again point to common interpretation errors. Finally, I discuss what should be reported in which context. The goal is to clarify concepts to avoid interpretation errors and propose reporting practices.

The Null Hypothesis Significance Testing framework

NHST is a method of statistical inference by which an experimental factor is tested against a hypothesis of no effect or no relationship based on a given observation. The method is a combination of the concepts of significance testing developed by Fisher in 1925 and of acceptance based on critical rejection regions developed by Neyman & Pearson in 1928 . In the following I am first presenting each approach, highlighting the key differences and common misconceptions that result from their combination into the NHST framework (for a more mathematical comparison, along with the Bayesian method, see Christensen, 2005 ). I next present the related concept of confidence intervals. I finish by discussing practical aspects in using NHST and reporting practice.

Fisher, significance testing, and the p-value

The method developed by ( Fisher, 1934 ; Fisher, 1955 ; Fisher, 1959 ) allows to compute the probability of observing a result at least as extreme as a test statistic (e.g. t value), assuming the null hypothesis of no effect is true. This probability or p-value reflects (1) the conditional probability of achieving the observed outcome or larger: p(Obs≥t|H0), and (2) is therefore a cumulative probability rather than a point estimate. It is equal to the area under the null probability distribution curve from the observed test statistic to the tail of the null distribution ( Turkheimer et al. , 2004 ). The approach proposed is of ‘proof by contradiction’ ( Christensen, 2005 ), we pose the null model and test if data conform to it.

In practice, it is recommended to set a level of significance (a theoretical p-value) that acts as a reference point to identify significant results, that is to identify results that differ from the null-hypothesis of no effect. Fisher recommended using p=0.05 to judge whether an effect is significant or not as it is roughly two standard deviations away from the mean for the normal distribution ( Fisher, 1934 page 45: ‘The value for which p=.05, or 1 in 20, is 1.96 or nearly 2; it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not’). A key aspect of Fishers’ theory is that only the null-hypothesis is tested, and therefore p-values are meant to be used in a graded manner to decide whether the evidence is worth additional investigation and/or replication ( Fisher, 1971 page 13: ‘it is open to the experimenter to be more or less exacting in respect of the smallness of the probability he would require […]’ and ‘no isolated experiment, however significant in itself, can suffice for the experimental demonstration of any natural phenomenon’). How small the level of significance is, is thus left to researchers.

What is not a p-value? Common mistakes

The p-value is not an indication of the strength or magnitude of an effect . Any interpretation of the p-value in relation to the effect under study (strength, reliability, probability) is wrong, since p-values are conditioned on H0. In addition, while p-values are randomly distributed (if all the assumptions of the test are met) when there is no effect, their distribution depends of both the population effect size and the number of participants, making impossible to infer strength of effect from them.

Similarly, 1-p is not the probability to replicate an effect . Often, a small value of p is considered to mean a strong likelihood of getting the same results on another try, but again this cannot be obtained because the p-value is not informative on the effect itself ( Miller, 2009 ). Because the p-value depends on the number of subjects, it can only be used in high powered studies to interpret results. In low powered studies (typically small number of subjects), the p-value has a large variance across repeated samples, making it unreliable to estimate replication ( Halsey et al. , 2015 ).

A (small) p-value is not an indication favouring a given hypothesis . Because a low p-value only indicates a misfit of the null hypothesis to the data, it cannot be taken as evidence in favour of a specific alternative hypothesis more than any other possible alternatives such as measurement error and selection bias ( Gelman, 2013 ). Some authors have even argued that the more (a priori) implausible the alternative hypothesis, the greater the chance that a finding is a false alarm ( Krzywinski & Altman, 2013 ; Nuzzo, 2014 ).

The p-value is not the probability of the null hypothesis p(H0), of being true, ( Krzywinski & Altman, 2013 ). This common misconception arises from a confusion between the probability of an observation given the null p(Obs≥t|H0) and the probability of the null given an observation p(H0|Obs≥t) that is then taken as an indication for p(H0) (see Nickerson, 2000 ).

Neyman-Pearson, hypothesis testing, and the α-value

Neyman & Pearson (1933) proposed a framework of statistical inference for applied decision making and quality control. In such framework, two hypotheses are proposed: the null hypothesis of no effect and the alternative hypothesis of an effect, along with a control of the long run probabilities of making errors. The first key concept in this approach, is the establishment of an alternative hypothesis along with an a priori effect size. This differs markedly from Fisher who proposed a general approach for scientific inference conditioned on the null hypothesis only. The second key concept is the control of error rates . Neyman & Pearson (1928) introduced the notion of critical intervals, therefore dichotomizing the space of possible observations into correct vs. incorrect zones. This dichotomization allows distinguishing correct results (rejecting H0 when there is an effect and not rejecting H0 when there is no effect) from errors (rejecting H0 when there is no effect, the type I error, and not rejecting H0 when there is an effect, the type II error). In this context, alpha is the probability of committing a Type I error in the long run. Alternatively, Beta is the probability of committing a Type II error in the long run.

The (theoretical) difference in terms of hypothesis testing between Fisher and Neyman-Pearson is illustrated on Figure 1 . In the 1 st case, we choose a level of significance for observed data of 5%, and compute the p-value. If the p-value is below the level of significance, it is used to reject H0. In the 2 nd case, we set a critical interval based on the a priori effect size and error rates. If an observed statistic value is below and above the critical values (the bounds of the confidence region), it is deemed significantly different from H0. In the NHST framework, the level of significance is (in practice) assimilated to the alpha level, which appears as a simple decision rule: if the p-value is less or equal to alpha, the null is rejected. It is however a common mistake to assimilate these two concepts. The level of significance set for a given sample is not the same as the frequency of acceptance alpha found on repeated sampling because alpha (a point estimate) is meant to reflect the long run probability whilst the p-value (a cumulative estimate) reflects the current probability ( Fisher, 1955 ; Hubbard & Bayarri, 2003 ).

An external file that holds a picture, illustration, etc.
Object name is f1000research-4-10487-g0000.jpg

The figure was prepared with G-power for a one-sided one-sample t-test, with a sample size of 32 subjects, an effect size of 0.45, and error rates alpha=0.049 and beta=0.80. In Fisher’s procedure, only the nil-hypothesis is posed, and the observed p-value is compared to an a priori level of significance. If the observed p-value is below this level (here p=0.05), one rejects H0. In Neyman-Pearson’s procedure, the null and alternative hypotheses are specified along with an a priori level of acceptance. If the observed statistical value is outside the critical region (here [-∞ +1.69]), one rejects H0.

Acceptance or rejection of H0?

The acceptance level α can also be viewed as the maximum probability that a test statistic falls into the rejection region when the null hypothesis is true ( Johnson, 2013 ). Therefore, one can only reject the null hypothesis if the test statistics falls into the critical region(s), or fail to reject this hypothesis. In the latter case, all we can say is that no significant effect was observed, but one cannot conclude that the null hypothesis is true. This is another common mistake in using NHST: there is a profound difference between accepting the null hypothesis and simply failing to reject it ( Killeen, 2005 ). By failing to reject, we simply continue to assume that H0 is true, which implies that one cannot argue against a theory from a non-significant result (absence of evidence is not evidence of absence). To accept the null hypothesis, tests of equivalence ( Walker & Nowacki, 2011 ) or Bayesian approaches ( Dienes, 2014 ; Kruschke, 2011 ) must be used.

Confidence intervals

Confidence intervals (CI) are builds that fail to cover the true value at a rate of alpha, the Type I error rate ( Morey & Rouder, 2011 ) and therefore indicate if observed values can be rejected by a (two tailed) test with a given alpha. CI have been advocated as alternatives to p-values because (i) they allow judging the statistical significance and (ii) provide estimates of effect size. Assuming the CI (a)symmetry and width are correct (but see Wilcox, 2012 ), they also give some indication about the likelihood that a similar value can be observed in future studies. For future studies of the same sample size, 95% CI give about 83% chance of replication success ( Cumming & Maillardet, 2006 ). If sample sizes however differ between studies, CI do not however warranty any a priori coverage.

Although CI provide more information, they are not less subject to interpretation errors (see Savalei & Dunn, 2015 for a review). The most common mistake is to interpret CI as the probability that a parameter (e.g. the population mean) will fall in that interval X% of the time. The correct interpretation is that, for repeated measurements with the same sample sizes, taken from the same population, X% of times the CI obtained will contain the true parameter value ( Tan & Tan, 2010 ). The alpha value has the same interpretation as testing against H0, i.e. we accept that 1-alpha CI are wrong in alpha percent of the times in the long run. This implies that CI do not allow to make strong statements about the parameter of interest (e.g. the mean difference) or about H1 ( Hoekstra et al. , 2014 ). To make a statement about the probability of a parameter of interest (e.g. the probability of the mean), Bayesian intervals must be used.

The (correct) use of NHST

NHST has always been criticized, and yet is still used every day in scientific reports ( Nickerson, 2000 ). One question to ask oneself is what is the goal of a scientific experiment at hand? If the goal is to establish a discrepancy with the null hypothesis and/or establish a pattern of order, because both requires ruling out equivalence, then NHST is a good tool ( Frick, 1996 ; Walker & Nowacki, 2011 ). If the goal is to test the presence of an effect and/or establish some quantitative values related to an effect, then NHST is not the method of choice since testing is conditioned on H0.

While a Bayesian analysis is suited to estimate that the probability that a hypothesis is correct, like NHST, it does not prove a theory on itself, but adds its plausibility ( Lindley, 2000 ). No matter what testing procedure is used and how strong results are, ( Fisher, 1959 p13) reminds us that ‘ […] no isolated experiment, however significant in itself, can suffice for the experimental demonstration of any natural phenomenon'. Similarly, the recent statement of the American Statistical Association ( Wasserstein & Lazar, 2016 ) makes it clear that conclusions should be based on the researchers understanding of the problem in context, along with all summary data and tests, and that no single value (being p-values, Bayesian factor or else) can be used support or invalidate a theory.

What to report and how?

Considering that quantitative reports will always have more information content than binary (significant or not) reports, we can always argue that raw and/or normalized effect size, confidence intervals, or Bayes factor must be reported. Reporting everything can however hinder the communication of the main result(s), and we should aim at giving only the information needed, at least in the core of a manuscript. Here I propose to adopt optimal reporting in the result section to keep the message clear, but have detailed supplementary material. When the hypothesis is about the presence/absence or order of an effect, and providing that a study has sufficient power, NHST is appropriate and it is sufficient to report in the text the actual p-value since it conveys the information needed to rule out equivalence. When the hypothesis and/or the discussion involve some quantitative value, and because p-values do not inform on the effect, it is essential to report on effect sizes ( Lakens, 2013 ), preferably accompanied with confidence or credible intervals. The reasoning is simply that one cannot predict and/or discuss quantities without accounting for variability. For the reader to understand and fully appreciate the results, nothing else is needed.

Because science progress is obtained by cumulating evidence ( Rosenthal, 1991 ), scientists should also consider the secondary use of the data. With today’s electronic articles, there are no reasons for not including all of derived data: mean, standard deviations, effect size, CI, Bayes factor should always be included as supplementary tables (or even better also share raw data). It is also essential to report the context in which tests were performed – that is to report all of the tests performed (all t, F, p values) because of the increase type one error rate due to selective reporting (multiple comparisons and p-hacking problems - Ioannidis, 2005 ). Providing all of this information allows (i) other researchers to directly and effectively compare their results in quantitative terms (replication of effects beyond significance, Open Science Collaboration, 2015 ), (ii) to compute power to future studies ( Lakens & Evers, 2014 ), and (iii) to aggregate results for meta-analyses whilst minimizing publication bias ( van Assen et al. , 2014 ).

[version 3; referees: 1 approved

Funding Statement

The author(s) declared that no grants were involved in supporting this work.

Christensen R: Testing Fisher, Neyman, Pearson, and Bayes. The American Statistician. 2005; 59 ( 2 ):121–126. 10.1198/000313005X20871 [ CrossRef ] [ Google Scholar ]
Cumming G, Maillardet R: Confidence intervals and replication: Where will the next mean fall? Psychological Methods. 2006; 11 ( 3 ):217–227. 10.1037/1082-989X.11.3.217 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Dienes Z: Using Bayes to get the most out of non-significant results. Front Psychol. 2014; 5 :781. 10.3389/fpsyg.2014.00781 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Fisher RA: Statistical Methods for Research Workers . (Vol. 5th Edition). Edinburgh, UK: Oliver and Boyd.1934. Reference Source [ Google Scholar ]
Fisher RA: Statistical Methods and Scientific Induction. Journal of the Royal Statistical Society, Series B. 1955; 17 ( 1 ):69–78. Reference Source [ Google Scholar ]
Fisher RA: Statistical methods and scientific inference . (2nd ed.). NewYork: Hafner Publishing,1959. Reference Source [ Google Scholar ]
Fisher RA: The Design of Experiments . Hafner Publishing Company, New-York.1971. Reference Source [ Google Scholar ]
Frick RW: The appropriate use of null hypothesis testing. Psychol Methods. 1996; 1 ( 4 ):379–390. 10.1037/1082-989X.1.4.379 [ CrossRef ] [ Google Scholar ]
Gelman A: P values and statistical practice. Epidemiology. 2013; 24 ( 1 ):69–72. 10.1097/EDE.0b013e31827886f7 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Halsey LG, Curran-Everett D, Vowler SL, et al.: The fickle P value generates irreproducible results. Nat Methods. 2015; 12 ( 3 ):179–85. 10.1038/nmeth.3288 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Hoekstra R, Morey RD, Rouder JN, et al.: Robust misinterpretation of confidence intervals. Psychon Bull Rev. 2014; 21 ( 5 ):1157–1164. 10.3758/s13423-013-0572-3 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Hubbard R, Bayarri MJ: Confusion over measures of evidence (p’s) versus errors ([alpha]’s) in classical statistical testing. The American Statistician. 2003; 57 ( 3 ):171–182. 10.1198/0003130031856 [ CrossRef ] [ Google Scholar ]
Ioannidis JP: Why most published research findings are false. PLoS Med. 2005; 2 ( 8 ):e124. 10.1371/journal.pmed.0020124 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Johnson VE: Revised standards for statistical evidence. Proc Natl Acad Sci U S A. 2013; 110 ( 48 ):19313–19317. 10.1073/pnas.1313476110 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Killeen PR: An alternative to null-hypothesis significance tests. Psychol Sci. 2005; 16 ( 5 ):345–353. 10.1111/j.0956-7976.2005.01538.x [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Kruschke JK: Bayesian Assessment of Null Values Via Parameter Estimation and Model Comparison. Perspect Psychol Sci. 2011; 6 ( 3 ):299–312. 10.1177/1745691611406925 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Krzywinski M, Altman N: Points of significance: Significance, P values and t -tests. Nat Methods. 2013; 10 ( 11 ):1041–1042. 10.1038/nmeth.2698 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Lakens D: Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t -tests and ANOVAs. Front Psychol. 2013; 4 :863. 10.3389/fpsyg.2013.00863 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Lakens D, Evers ER: Sailing From the Seas of Chaos Into the Corridor of Stability: Practical Recommendations to Increase the Informational Value of Studies. Perspect Psychol Sci. 2014; 9 ( 3 ):278–292. 10.1177/1745691614528520 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Lindley D: The philosophy of statistics. Journal of the Royal Statistical Society. 2000; 49 ( 3 ):293–337. 10.1111/1467-9884.00238 [ CrossRef ] [ Google Scholar ]
Miller J: What is the probability of replicating a statistically significant effect? Psychon Bull Rev. 2009; 16 ( 4 ):617–640. 10.3758/PBR.16.4.617 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Morey RD, Rouder JN: Bayes factor approaches for testing interval null hypotheses. Psychol Methods. 2011; 16 ( 4 ):406–419. 10.1037/a0024377 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Neyman J, Pearson ES: On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference: Part I. Biometrika. 1928; 20A ( 1/2 ):175–240. 10.3389/fpsyg.2015.00245 [ CrossRef ] [ Google Scholar ]
Neyman J, Pearson ES: On the problem of the most efficient tests of statistical hypotheses. Philos Trans R Soc Lond Ser A. 1933; 231 ( 694–706 ):289–337. 10.1098/rsta.1933.0009 [ CrossRef ] [ Google Scholar ]
Nickerson RS: Null hypothesis significance testing: a review of an old and continuing controversy. Psychol Methods. 2000; 5 ( 2 ):241–301. 10.1037/1082-989X.5.2.241 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Nuzzo R: Scientific method: statistical errors. Nature. 2014; 506 ( 7487 ):150–152. 10.1038/506150a [ PubMed ] [ CrossRef ] [ Google Scholar ]
Open Science Collaboration. PSYCHOLOGY. Estimating the reproducibility of psychological science. Science. 2015; 349 ( 6251 ):aac4716. 10.1126/science.aac4716 [ PubMed ] [ CrossRef ] [ Google Scholar ]
Rosenthal R: Cumulating psychology: an appreciation of Donald T. Campbell. Psychol Sci. 1991; 2 ( 4 ):213–221. 10.1111/j.1467-9280.1991.tb00138.x [ CrossRef ] [ Google Scholar ]
Savalei V, Dunn E: Is the call to abandon p -values the red herring of the replicability crisis? Front Psychol. 2015; 6 :245. 10.3389/fpsyg.2015.00245 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Tan SH, Tan SB: The Correct Interpretation of Confidence Intervals. Proceedings of Singapore Healthcare. 2010; 19 ( 3 ):276–278. 10.1177/201010581001900316 [ CrossRef ] [ Google Scholar ]
Turkheimer FE, Aston JA, Cunningham VJ: On the logic of hypothesis testing in functional imaging. Eur J Nucl Med Mol Imaging. 2004; 31 ( 5 ):725–732. 10.1007/s00259-003-1387-7 [ PubMed ] [ CrossRef ] [ Google Scholar ]
van Assen MA, van Aert RC, Nuijten MB, et al.: Why Publishing Everything Is More Effective than Selective Publishing of Statistically Significant Results. PLoS One. 2014; 9 ( 1 ):e84896. 10.1371/journal.pone.0084896 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Walker E, Nowacki AS: Understanding equivalence and noninferiority testing. J Gen Intern Med. 2011; 26 ( 2 ):192–196. 10.1007/s11606-010-1513-8 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
Wasserstein RL, Lazar NA: The ASA’s Statement on p -Values: Context, Process, and Purpose. The American Statistician. 2016; 70 ( 2 ):129–133. 10.1080/00031305.2016.1154108 [ CrossRef ] [ Google Scholar ]
Wilcox R: Introduction to Robust Estimation and Hypothesis Testing . Edition 3, Academic Press, Elsevier: Oxford, UK, ISBN: 978-0-12-386983-8.2012. Reference Source [ Google Scholar ]

Referee response for version 3

Dorothy vera margaret bishop.

1 Department of Experimental Psychology, University of Oxford, Oxford, UK

I can see from the history of this paper that the author has already been very responsive to reviewer comments, and that the process of revising has now been quite protracted.

That makes me reluctant to suggest much more, but I do see potential here for making the paper more impactful. So my overall view is that, once a few typos are fixed (see below), this could be published as is, but I think there is an issue with the potential readership and that further revision could overcome this.

I suspect my take on this is rather different from other reviewers, as I do not regard myself as a statistics expert, though I am on the more quantitative end of the continuum of psychologists and I try to keep up to date. I think I am quite close to the target readership , insofar as I am someone who was taught about statistics ages ago and uses stats a lot, but never got adequate training in the kinds of topic covered by this paper. The fact that I am aware of controversies around the interpretation of confidence intervals etc is simply because I follow some discussions of this on social media. I am therefore very interested to have a clear account of these issues.

This paper contains helpful information for someone in this position, but it is not always clear, and I felt the relevance of some of the content was uncertain. So here are some recommendations:

As one previous reviewer noted, it’s questionable that there is a need for a tutorial introduction, and the limited length of this article does not lend itself to a full explanation. So it might be better to just focus on explaining as clearly as possible the problems people have had in interpreting key concepts. I think a title that made it clear this was the content would be more appealing than the current one.
P 3, col 1, para 3, last sentence. Although statisticians always emphasise the arbitrary nature of p < .05, we all know that in practice authors who use other values are likely to have their analyses queried. I wondered whether it would be useful here to note that in some disciplines different cutoffs are traditional, e.g. particle physics. Or you could cite David Colquhoun’s paper in which he recommends using p < .001 ( http://rsos.royalsocietypublishing.org/content/1/3/140216) - just to be clear that the traditional p < .05 has been challenged.

What I can’t work out is how you would explain the alpha from Neyman-Pearson in the same way (though I can see from Figure 1 that with N-P you could test an alternative hypothesis, such as the idea that the coin would be heads 75% of the time).

‘By failing to reject, we simply continue to assume that H0 is true, which implies that one cannot….’ have ‘In failing to reject, we do not assume that H0 is true; one cannot argue against a theory from a non-significant result.’

I felt most readers would be interested to read about tests of equivalence and Bayesian approaches, but many would be unfamiliar with these and might like to see an example of how they work in practice – if space permitted.

Confidence intervals: I simply could not understand the first sentence – I wondered what was meant by ‘builds’ here. I understand about difficulties in comparing CI across studies when sample sizes differ, but I did not find the last sentence on p 4 easy to understand.
P 5: The sentence starting: ‘The alpha value has the same interpretation’ was also hard to understand, especially the term ‘1-alpha CI’. Here too I felt some concrete illustration might be helpful to the reader. And again, I also found the reference to Bayesian intervals tantalising – I think many readers won’t know how to compute these and something like a figure comparing a traditional CI with a Bayesian interval and giving a source for those who want to read on would be very helpful. The reference to ‘credible intervals’ in the penultimate paragraph is very unclear and needs a supporting reference – most readers will not be familiar with this concept.

P 3, col 1, para 2, line 2; “allows us to compute”

P 3, col 2, para 2, ‘probability of replicating’

P 3, col 2, para 2, line 4 ‘informative about’

P 3, col 2, para 4, line 2 delete ‘of’

P 3, col 2, para 5, line 9 – ‘conditioned’ is either wrong or too technical here: would ‘based’ be acceptable as alternative wording

P 3, col 2, para 5, line 13 ‘This dichotomisation allows one to distinguish’

P 3, col 2, para 5, last sentence, delete ‘Alternatively’.

P 3, col 2, last para line 2 ‘first’

P 4, col 2, para 2, last sentence is hard to understand; not sure if this is better: ‘If sample sizes differ between studies, the distribution of CIs cannot be specified a priori’

P 5, col 1, para 2, ‘a pattern of order’ – I did not understand what was meant by this

P 5, col 1, para 2, last sentence unclear: possible rewording: “If the goal is to test the size of an effect then NHST is not the method of choice, since testing can only reject the null hypothesis.’ (??)

P 5, col 1, para 3, line 1 delete ‘that’

P 5, col 1, para 3, line 3 ‘on’ -> ‘by’

P 5, col 2, para 1, line 4 , rather than ‘Here I propose to adopt’ I suggest ‘I recommend adopting’

P 5, col 2, para 1, line 13 ‘with’ -> ‘by’

P 5, col 2, para 1 – recommend deleting last sentence

P 5, col 2, para 2, line 2 ‘consider’ -> ‘anticipate’

P 5, col 2, para 2, delete ‘should always be included’

P 5, col 2, para 2, ‘type one’ -> ‘Type I’

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

The University of Edinburgh, UK

I wondered about changing the focus slightly and modifying the title to reflect this to say something like: Null hypothesis significance testing: a guide to commonly misunderstood concepts and recommendations for good practice

Thank you for the suggestion – you indeed saw the intention behind the ‘tutorial’ style of the paper.

P 3, col 1, para 3, last sentence. Although statisticians always emphasise the arbitrary nature of p < .05, we all know that in practice authors who use other values are likely to have their analyses queried. I wondered whether it would be useful here to note that in some disciplines different cutoffs are traditional, e.g. particle physics. Or you could cite David Colquhoun’s paper in which he recommends using p < .001 ( http://rsos.royalsocietypublishing.org/content/1/3/140216) - just to be clear that the traditional p < .05 has been challenged.

I have added a sentence on this citing Colquhoun 2014 and the new Benjamin 2017 on using .005.

I agree that this point is always hard to appreciate, especially because it seems like in practice it makes little difference. I added a paragraph but using reaction times rather than a coin toss – thanks for the suggestion.

Added an example based on new table 1, following figure 1 – giving CI, equivalence tests and Bayes Factor (with refs to easy to use tools)

Changed builds to constructs (this simply means they are something we build) and added that the implication that probability coverage is not warranty when sample size change, is that we cannot compare CI.

I changed ‘ i.e. we accept that 1-alpha CI are wrong in alpha percent of the times in the long run’ to ‘, ‘e.g. a 95% CI is wrong in 5% of the times in the long run (i.e. if we repeat the experiment many times).’ – for Bayesian intervals I simply re-cited Morey & Rouder, 2011.

It is not the CI cannot be specified, it’s that the interval is not predictive of anything anymore! I changed it to ‘If sample sizes, however, differ between studies, there is no warranty that a CI from one study will be true at the rate alpha in a different study, which implies that CI cannot be compared across studies at this is rarely the same sample sizes’

I added (i.e. establish that A > B) – we test that conditions are ordered, but without further specification of the probability of that effect nor its size

Yes it works – thx

P 5, col 2, para 2, ‘type one’ -> ‘Type I’

Typos fixed, and suggestions accepted – thanks for that.

Stephen J. Senn

1 Luxembourg Institute of Health, Strassen, L-1445, Luxembourg

The revisions are OK for me, and I have changed my status to Approved.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Referee response for version 2

On the whole I think that this article is reasonable, my main reservation being that I have my doubts on whether the literature needs yet another tutorial on this subject.

A further reservation I have is that the author, following others, stresses what in my mind is a relatively unimportant distinction between the Fisherian and Neyman-Pearson (NP) approaches. The distinction stressed by many is that the NP approach leads to a dichotomy accept/reject based on probabilities established in advance, whereas the Fisherian approach uses tail area probabilities calculated from the observed statistic. I see this as being unimportant and not even true. Unless one considers that the person carrying out a hypothesis test (original tester) is mandated to come to a conclusion on behalf of all scientific posterity, then one must accept that any remote scientist can come to his or her conclusion depending on the personal type I error favoured. To operate the results of an NP test carried out by the original tester, the remote scientist then needs to know the p-value. The type I error rate is then compared to this to come to a personal accept or reject decision (1). In fact Lehmann (2), who was an important developer of and proponent of the NP system, describes exactly this approach as being good practice. (See Testing Statistical Hypotheses, 2nd edition P70). Thus using tail-area probabilities calculated from the observed statistics does not constitute an operational difference between the two systems.

A more important distinction between the Fisherian and NP systems is that the former does not use alternative hypotheses(3). Fisher's opinion was that the null hypothesis was more primitive than the test statistic but that the test statistic was more primitive than the alternative hypothesis. Thus, alternative hypotheses could not be used to justify choice of test statistic. Only experience could do that.

Further distinctions between the NP and Fisherian approach are to do with conditioning and whether a null hypothesis can ever be accepted.

I have one minor quibble about terminology. As far as I can see, the author uses the usual term 'null hypothesis' and the eccentric term 'nil hypothesis' interchangeably. It would be simpler if the latter were abandoned.

Referee response for version 1

Marcel alm van assen.

1 Department of Methodology and Statistics, Tilburgh University, Tilburg, Netherlands

Null hypothesis significance testing (NHST) is a difficult topic, with misunderstandings arising easily. Many texts, including basic statistics books, deal with the topic, and attempt to explain it to students and anyone else interested. I would refer to a good basic text book, for a detailed explanation of NHST, or to a specialized article when wishing an explaining the background of NHST. So, what is the added value of a new text on NHST? In any case, the added value should be described at the start of this text. Moreover, the topic is so delicate and difficult that errors, misinterpretations, and disagreements are easy. I attempted to show this by giving comments to many sentences in the text.

Abstract: “null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely”. No, NHST is the method to test the hypothesis of no effect.

Intro: “Null hypothesis significance testing (NHST) is a method of statistical inference by which an observation is tested against a hypothesis of no effect or no relationship.” What is an ‘observation’? NHST is difficult to describe in one sentence, particularly here. I would skip this sentence entirely, here.

Section on Fisher; also explain the one-tailed test.

Section on Fisher; p(Obs|H0) does not reflect the verbal definition (the ‘or more extreme’ part).

Section on Fisher; use a reference and citation to Fisher’s interpretation of the p-value

Section on Fisher; “This was however only intended to be used as an indication that there is something in the data that deserves further investigation. The reason for this is that only H0 is tested whilst the effect under study is not itself being investigated.” First sentence, can you give a reference? Many people say a lot about Fisher’s intentions, but the good man is dead and cannot reply… Second sentence is a bit awkward, because the effect is investigated in a way, by testing the H0.

Section on p-value; Layout and structure can be improved greatly, by first again stating what the p-value is, and then statement by statement, what it is not, using separate lines for each statement. Consider adding that the p-value is randomly distributed under H0 (if all the assumptions of the test are met), and that under H1 the p-value is a function of population effect size and N; the larger each is, the smaller the p-value generally is.

Skip the sentence “If there is no effect, we should replicate the absence of effect with a probability equal to 1-p”. Not insightful, and you did not discuss the concept ‘replicate’ (and do not need to).

Skip the sentence “The total probability of false positives can also be obtained by aggregating results ( Ioannidis, 2005 ).” Not strongly related to p-values, and introduces unnecessary concepts ‘false positives’ (perhaps later useful) and ‘aggregation’.

Consider deleting; “If there is an effect however, the probability to replicate is a function of the (unknown) population effect size with no good way to know this from a single experiment ( Killeen, 2005 ).”

The following sentence; “ Finally, a (small) p-value is not an indication favouring a hypothesis . A low p-value indicates a misfit of the null hypothesis to the data and cannot be taken as evidence in favour of a specific alternative hypothesis more than any other possible alternatives such as measurement error and selection bias ( Gelman, 2013 ).” is surely not mainstream thinking about NHST; I would surely delete that sentence. In NHST, a p-value is used for testing the H0. Why did you not yet discuss significance level? Yes, before discussing what is not a p-value, I would explain NHST (i.e., what it is and how it is used).

Also the next sentence “The more (a priori) implausible the alternative hypothesis, the greater the chance that a finding is a false alarm ( Krzywinski & Altman, 2013 ; Nuzzo, 2014 ).“ is not fully clear to me. This is a Bayesian statement. In NHST, no likelihoods are attributed to hypotheses; the reasoning is “IF H0 is true, then…”.

Last sentence: “As Nickerson (2000) puts it ‘theory corroboration requires the testing of multiple predictions because the chance of getting statistically significant results for the wrong reasons in any given case is high’.” What is relation of this sentence to the contents of this section, precisely?

Next section: “For instance, we can estimate that the probability of a given F value to be in the critical interval [+2 +∞] is less than 5%” This depends on the degrees of freedom.

“When there is no effect (H0 is true), the erroneous rejection of H0 is known as type I error and is equal to the p-value.” Strange sentence. The Type I error is the probability of erroneously rejecting the H0 (so, when it is true). The p-value is … well, you explained it before; it surely does not equal the Type I error.

Consider adding a figure explaining the distinction between Fisher’s logic and that of Neyman and Pearson.

“When the test statistics falls outside the critical region(s)” What is outside?

“There is a profound difference between accepting the null hypothesis and simply failing to reject it ( Killeen, 2005 )” I agree with you, but perhaps you may add that some statisticians simply define “accept H0’” as obtaining a p-value larger than the significance level. Did you already discuss the significance level, and it’s mostly used values?

“To accept or reject equally the null hypothesis, Bayesian approaches ( Dienes, 2014 ; Kruschke, 2011 ) or confidence intervals must be used.” Is ‘reject equally’ appropriate English? Also using Cis, one cannot accept the H0.

Do you start discussing alpha only in the context of Cis?

“CI also indicates the precision of the estimate of effect size, but unless using a percentile bootstrap approach, they require assumptions about distributions which can lead to serious biases in particular regarding the symmetry and width of the intervals ( Wilcox, 2012 ).” Too difficult, using new concepts. Consider deleting.

“Assuming the CI (a)symmetry and width are correct, this gives some indication about the likelihood that a similar value can be observed in future studies, with 95% CI giving about 83% chance of replication success ( Lakens & Evers, 2014 ).” This statement is, in general, completely false. It very much depends on the sample sizes of both studies. If the replication study has a much, much, much larger N, then the probability that the original CI will contain the effect size of the replication approaches (1-alpha)*100%. If the original study has a much, much, much larger N, then the probability that the original Ci will contain the effect size of the replication study approaches 0%.

“Finally, contrary to p-values, CI can be used to accept H0. Typically, if a CI includes 0, we cannot reject H0. If a critical null region is specified rather than a single point estimate, for instance [-2 +2] and the CI is included within the critical null region, then H0 can be accepted. Importantly, the critical region must be specified a priori and cannot be determined from the data themselves.” No. H0 cannot be accepted with Cis.

“The (posterior) probability of an effect can however not be obtained using a frequentist framework.” Frequentist framework? You did not discuss that, yet.

“X% of times the CI obtained will contain the same parameter value”. The same? True, you mean?

“e.g. X% of the times the CI contains the same mean” I do not understand; which mean?

“The alpha value has the same interpretation as when using H0, i.e. we accept that 1-alpha CI are wrong in alpha percent of the times. “ What do you mean, CI are wrong? Consider rephrasing.

“To make a statement about the probability of a parameter of interest, likelihood intervals (maximum likelihood) and credibility intervals (Bayes) are better suited.” ML gives the likelihood of the data given the parameter, not the other way around.

“Many of the disagreements are not on the method itself but on its use.” Bayesians may disagree.

“If the goal is to establish the likelihood of an effect and/or establish a pattern of order, because both requires ruling out equivalence, then NHST is a good tool ( Frick, 1996 )” NHST does not provide evidence on the likelihood of an effect.

“If the goal is to establish some quantitative values, then NHST is not the method of choice.” P-values are also quantitative… this is not a precise sentence. And NHST may be used in combination with effect size estimation (this is even recommended by, e.g., the American Psychological Association (APA)).

“Because results are conditioned on H0, NHST cannot be used to establish beliefs.” It can reinforce some beliefs, e.g., if H0 or any other hypothesis, is true.

“To estimate the probability of a hypothesis, a Bayesian analysis is a better alternative.” It is the only alternative?

“Note however that even when a specific quantitative prediction from a hypothesis is shown to be true (typically testing H1 using Bayes), it does not prove the hypothesis itself, it only adds to its plausibility.” How can we show something is true?

I do not agree on the contents of the last section on ‘minimal reporting’. I prefer ‘optimal reporting’ instead, i.e., the reporting the information that is essential to the interpretation of the result, to any ready, which may have other goals than the writer of the article. This reporting includes, for sure, an estimate of effect size, and preferably a confidence interval, which is in line with recommendations of the APA.

I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

The idea of this short review was to point to common interpretation errors (stressing again and again that we are under H0) being in using p-values or CI, and also proposing reporting practices to avoid bias. This is now stated at the end of abstract.

Regarding text books, it is clear that many fail to clearly distinguish Fisher/Pearson/NHST, see Glinet et al (2012) J. Exp Education 71, 83-92. If you have 1 or 2 in mind that you know to be good, I’m happy to include them.

I agree – yet people use it to investigate (not test) if an effect is likely. The issue here is wording. What about adding this distinction at the end of the sentence?: ‘null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences used to investigate if an effect is likely, even though it actually tests for the hypothesis of no effect’.

I think a definition is needed, as it offers a starting point. What about the following: ‘NHST is a method of statistical inference by which an experimental factor is tested against a hypothesis of no effect or no relationship based on a given observation’

The section on Fisher has been modified (more or less) as suggested: (1) avoiding talking about one or two tailed tests (2) updating for p(Obs≥t|H0) and (3) referring to Fisher more explicitly (ie pages from articles and book) ; I cannot tell his intentions but these quotes leave little space to alternative interpretations.

The reasoning here is as you state yourself, part 1: ‘a p-value is used for testing the H0; and part 2: ‘no likelihoods are attributed to hypotheses’ it follows we cannot favour a hypothesis. It might seems contentious but this is the case that all we can is to reject the null – how could we favour a specific alternative hypothesis from there? This is explored further down the manuscript (and I now point to that) – note that we do not need to be Bayesian to favour a specific H1, all I’m saying is this cannot be attained with a p-value.

The point was to emphasise that a p value is not there to tell us a given H1 is true and can only be achieved through multiple predictions and experiments. I deleted it for clarity.

This sentence has been removed

Indeed, you are right and I have modified the text accordingly. When there is no effect (H0 is true), the erroneous rejection of H0 is known as type 1 error. Importantly, the type 1 error rate, or alpha value is determined a priori. It is a common mistake but the level of significance (for a given sample) is not the same as the frequency of acceptance alpha found on repeated sampling (Fisher, 1955).

A figure is now presented – with levels of acceptance, critical region, level of significance and p-value.

I should have clarified further here – as I was having in mind tests of equivalence. To clarify, I simply states now: ‘To accept the null hypothesis, tests of equivalence or Bayesian approaches must be used.’

It is now presented in the paragraph before.

Yes, you are right, I completely overlooked this problem. The corrected sentence (with more accurate ref) is now “Assuming the CI (a)symmetry and width are correct, this gives some indication about the likelihood that a similar value can be observed in future studies. For future studies of the same sample size, 95% CI giving about 83% chance of replication success (Cumming and Mallardet, 2006). If sample sizes differ between studies, CI do not however warranty any a priori coverage”.

Again, I had in mind equivalence testing, but in both cases you are right we can only reject and I therefore removed that sentence.

Yes, p-values must be interpreted in context with effect size, but this is not what people do. The point here is to be pragmatic, does and don’t. The sentence was changed.

Not for testing, but for probability, I am not aware of anything else.

Cumulative evidence is, in my opinion, the only way to show it. Even in hard science like physics multiple experiments. In the recent CERN study on finding Higgs bosons, 2 different and complementary experiments ran in parallel – and the cumulative evidence was taken as a proof of the true existence of Higgs bosons.

Daniel Lakens

1 School of Innovation Sciences, Eindhoven University of Technology, Eindhoven, Netherlands

I appreciate the author's attempt to write a short tutorial on NHST. Many people don't know how to use it, so attempts to educate people are always worthwhile. However, I don't think the current article reaches it's aim. For one, I think it might be practically impossible to explain a lot in such an ultra short paper - every section would require more than 2 pages to explain, and there are many sections. Furthermore, there are some excellent overviews, which, although more extensive, are also much clearer (e.g., Nickerson, 2000 ). Finally, I found many statements to be unclear, and perhaps even incorrect (noted below). Because there is nothing worse than creating more confusion on such a topic, I have extremely high standards before I think such a short primer should be indexed. I note some examples of unclear or incorrect statements below. I'm sorry I can't make a more positive recommendation.

“investigate if an effect is likely” – ambiguous statement. I think you mean, whether the observed DATA is probable, assuming there is no effect?

The Fisher (1959) reference is not correct – Fischer developed his method much earlier.

“This p-value thus reflects the conditional probability of achieving the observed outcome or larger, p(Obs|H0)” – please add 'assuming the null-hypothesis is true'.

“p(Obs|H0)” – explain this notation for novices.

“Following Fisher, the smaller the p-value, the greater the likelihood that the null hypothesis is false.” This is wrong, and any statement about this needs to be much more precise. I would suggest direct quotes.

“there is something in the data that deserves further investigation” –unclear sentence.

“The reason for this” – unclear what ‘this’ refers to.

“ not the probability of the null hypothesis of being true, p(H0)” – second of can be removed?

“Any interpretation of the p-value in relation to the effect under study (strength, reliability, probability) is indeed

wrong, since the p-value is conditioned on H0” - incorrect. A big problem is that it depends on the sample size, and that the probability of a theory depends on the prior.

“If there is no effect, we should replicate the absence of effect with a probability equal to 1-p.” I don’t understand this, but I think it is incorrect.

“The total probability of false positives can also be obtained by aggregating results (Ioannidis, 2005).” Unclear, and probably incorrect.

“By failing to reject, we simply continue to assume that H0 is true, which implies that one cannot, from a nonsignificant result, argue against a theory” – according to which theory? From a NP perspective, you can ACT as if the theory is false.

“(Lakens & Evers, 2014”) – we are not the original source, which should be cited instead.

“ Typically, if a CI includes 0, we cannot reject H0.” - when would this not be the case? This assumes a CI of 1-alpha.

“If a critical null region is specified rather than a single point estimate, for instance [-2 +2] and the CI is included within the critical null region, then H0 can be accepted.” – you mean practically, or formally? I’m pretty sure only the former.

The section on ‘The (correct) use of NHST’ seems to conclude only Bayesian statistics should be used. I don’t really agree.

“ we can always argue that effect size, power, etc. must be reported.” – which power? Post-hoc power? Surely not? Other types are unknown. So what do you mean?

The recommendation on what to report remains vague, and it is unclear why what should be reported.

This sentence was changed, following as well the other reviewer, to ‘null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely, even though it actually tests whether the observed data are probable, assuming there is no effect’

Changed, refers to Fisher 1925

I changed a little the sentence structure, which should make explicit that this is the condition probability.

This has been changed to ‘[…] to decide whether the evidence is worth additional investigation and/or replication (Fisher, 1971 p13)’

my mistake – the sentence structure is now ‘ not the probability of the null hypothesis p(H0), of being true,’ ; hope this makes more sense (and this way refers back to p(Obs>t|H0)

Fair enough – my point was to stress the fact that p value and effect size or H1 have very little in common, but yes that the part in common has to do with sample size. I left the conditioning on H0 but also point out the dependency on sample size.

The whole paragraph was changed to reflect a more philosophical take on scientific induction/reasoning. I hope this is clearer.

Changed to refer to equivalence testing

I rewrote this, as to show frequentist analysis can be used - I’m trying to sell Bayes more than any other approach.

I’m arguing we should report it all, that’s why there is no exhausting list – I can if needed.

Null hypothesis

by Marco Taboga , PhD

In a test of hypothesis , a sample of data is used to decide whether to reject or not to reject a hypothesis about the probability distribution from which the sample was extracted.

The hypothesis is called the null hypothesis, or simply "the null".

Things a data scientist should know: 1) the criminal trial analogy; 2) the role of the test statistic; 3) failure to reject may be due to lack of power; 4) Rejection may be due to misspecification.

Table of contents

The null is like the defendant in a criminal trial

How is the null hypothesis tested, example 1 - proportion of defective items, measurement, test statistic, critical region, interpretation, example 2 - reliability of a production plant, rejection and failure to reject, not rejecting and accepting are not the same thing, failure to reject can be due to lack of power, rejections are easier to interpret, but be careful, takeaways - how to (and not to) formulate a null hypothesis, more examples, more details, best practices in science, keep reading the glossary.

Formulating null hypotheses and subjecting them to statistical testing is one of the workhorses of the scientific method.

Scientists in all fields make conjectures about the phenomena they study, translate them into null hypotheses and gather data to test them.

This process resembles a trial:

the defendant (the null hypothesis) is accused of being guilty (wrong);

evidence (data) is gathered in order to prove the defendant guilty (reject the null);

if there is evidence beyond any reasonable doubt, the defendant is found guilty (the null is rejected);

otherwise, the defendant is found not guilty (the null is not rejected).

Keep this analogy in mind because it helps to better understand statistical tests, their limitations, use and misuse, and frequent misinterpretation.

The null hypothesis is like the defendant in a criminal trial.

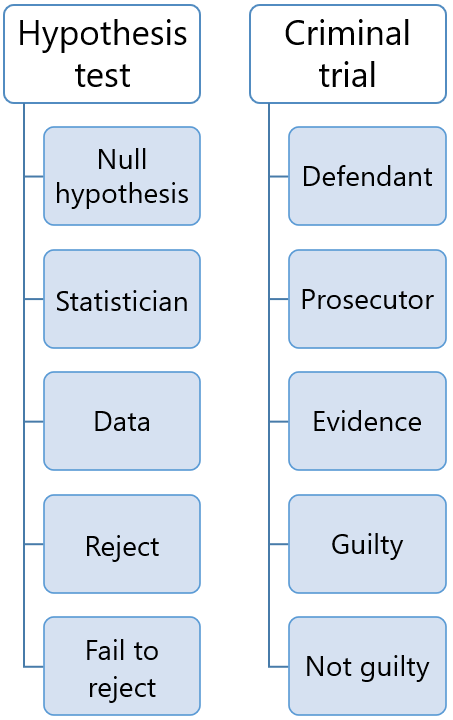
Before collecting the data:

we decide how to summarize the relevant characteristics of the sample data in a single number, the so-called test statistic ;

we derive the probability distribution of the test statistic under the hypothesis that the null is true (the data is regarded as random; therefore, the test statistic is a random variable);

we decide what probability of incorrectly rejecting the null we are willing to tolerate (the level of significance , or size of the test ); the level of significance is typically a small number, such as 5% or 1%.

we choose one or more intervals of values (collectively called rejection region) such that the probability that the test statistic falls within these intervals is equal to the desired level of significance; the rejection region is often a tail of the distribution of the test statistic (one-tailed test) or the union of the left and right tails (two-tailed test).

The rejection region is a set of values that the test statistic is unlikely to take if the null hypothesis is true.

Then, the data is collected and used to compute the value of the test statistic.

A decision is taken as follows:

if the test statistic falls within the rejection region, then the null hypothesis is rejected;

otherwise, it is not rejected.

The probability distribution of the test statistic and the rejection region depend on the null hypothesis.

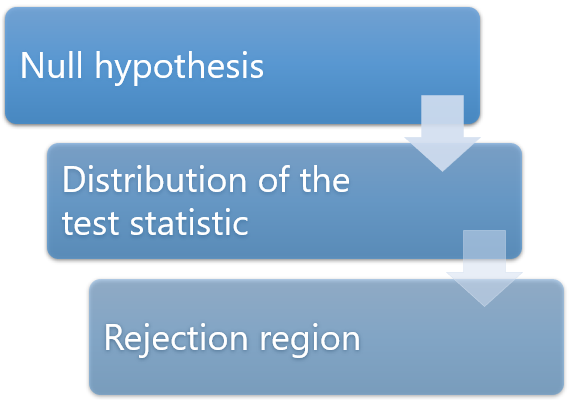
We now make two examples of practical problems that lead to formulate and test a null hypothesis.

A new method is proposed to produce light bulbs.

The proponents claim that it produces less defective bulbs than the method currently in use.

To check the claim, we can set up a statistical test as follows.

We keep the light bulbs on for 10 consecutive days, and then we record whether they are still working at the end of the test period.

The probability that a light bulb produced with the new method is still working at the end of the test period is the same as that of a light bulb produced with the old method.

100 light bulbs are tested:

50 of them are produced with the new method (group A)

the remaining 50 are produced with the old method (group B).

The final data comprises 100 observations of:

an indicator variable which is equal to 1 if the light bulb is still working at the end of the test period and 0 otherwise;

a categorical variable that records the group (A or B) to which each light bulb belongs.

We use the data to compute the proportions of working light bulbs in groups A and B.

The proportions are estimates of the probabilities of not being defective, which are equal for the two groups under the null hypothesis.

We then compute a z-statistic (see here for details) by:

taking the difference between the proportion in group A and the proportion in group B;

standardizing the difference:

we subtract the expected value (which is zero under the null hypothesis);

we divide by the standard deviation (it can be derived analytically).

The distribution of the z-statistic can be approximated by a standard normal distribution .

The z-statistic has a normal distribution with zero mean and variance equal to one.

We decide that the level of confidence must be 5%. In other words, we are going to tolerate a 5% probability of incorrectly rejecting the null hypothesis.

The critical region is the right 5%-tail of the normal distribution, that is, the set of all values greater than 1.645 (see the glossary entry on critical values if you are wondering how this value was obtained).

If the test statistic is greater than 1.645, then the null hypothesis is rejected; otherwise, it is not rejected.

A rejection is interpreted as significant evidence that the new production method produces less defective items; failure to reject is interpreted as insufficient evidence that the new method is better.

The null hypothesis is rejected when the test statistic falls in the tails of the distribution.

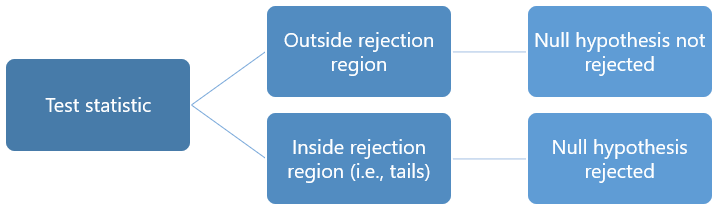
A production plant incurs high costs when production needs to be halted because some machinery fails.

The plant manager has decided that he is not willing to tolerate more than one halt per year on average.

If the expected number of halts per year is greater than 1, he will make new investments in order to improve the reliability of the plant.

A statistical test is set up as follows.

The reliability of the plant is measured by the number of halts.

The number of halts in a year is assumed to have a Poisson distribution with expected value equal to 1 (using the Poisson distribution is common in reliability testing).

The manager cannot wait more than one year before taking a decision.

There will be a single datum at his disposal: the number of halts observed during one year.

The number of halts is used as a test statistic. By assumption, it has a Poisson distribution under the null hypothesis.

The manager decides that the probability of incorrectly rejecting the null can be at most 10%.

A Poisson random variable with expected value equal to 1 takes values:

larger than 1 with probability 26.42%;

larger than 2 with probability 8.03%.

Therefore, it is decided that the critical region will be the set of all values greater than or equal to 3.

If the test statistic is strictly greater than or equal to 3, then the null is rejected; otherwise, it is not rejected.

A rejection is interpreted as significant evidence that the production plant is not reliable enough (the average number of halts per year is significantly larger than tolerated).

Failure to reject is interpreted as insufficient evidence that the plant is unreliable.

Failure to reject the null hypothesis is interpreted as insufficient evidence.

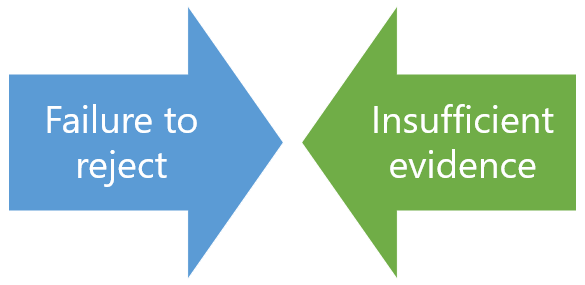
This section discusses the main problems that arise in the interpretation of the outcome of a statistical test (reject / not reject).

When the test statistic does not fall within the critical region, then we do not reject the null hypothesis.

Does this mean that we accept the null? Not really.

In general, failure to reject does not constitute, per se, strong evidence that the null hypothesis is true .

Remember the analogy between hypothesis testing and a criminal trial. In a trial, when the defendant is declared not guilty, this does not mean that the defendant is innocent. It only means that there was not enough evidence (not beyond any reasonable doubt) against the defendant.

In turn, lack of evidence can be due:

either to the fact that the defendant is innocent ;

or to the fact that the prosecution has not been able to provide enough evidence against the defendant, even if the latter is guilty .

This is the very reason why courts do not declare defendants innocent, but they use the locution "not guilty".

In a similar fashion, statisticians do not say that the null hypothesis has been accepted, but they say that it has not been rejected.

Failure to reject does not imply acceptance.

To better understand why failure to reject does not in general constitute strong evidence that the null hypothesis is true, we need to use the concept of statistical power .

The power of a test is the probability (calculated ex-ante, i.e., before observing the data) that the null will be rejected when another hypothesis (called the alternative hypothesis ) is true.

Let's consider the first of the two examples above (the production of light bulbs).

In that example, the null hypothesis is: the probability that a light bulb is defective does not decrease after introducing a new production method.

Let's make the alternative hypothesis that the probability of being defective is 1% smaller after changing the production process (assume that a 1% decrease is considered a meaningful improvement by engineers).

How much is the ex-ante probability of rejecting the null if the alternative hypothesis is true?

If this probability (the power of the test) is small, then it is very likely that we will not reject the null even if it is wrong.

If we use the analogy with criminal trials, low power means that most likely the prosecution will not be able to provide sufficient evidence, even if the defendant is guilty.

Thus, in the case of lack of power, failure to reject is almost meaningless (it was anyway highly likely).

This is why, before performing a test, it is good statistical practice to compute its power against a relevant alternative .

If the power is found to be too small, there are usually remedies. In particular, statistical power can usually be increased by increasing the sample size (see, e.g., the lecture on hypothesis tests about the mean ).

The best practice is to compute the power of the test, that is, the probability of rejecting the null hypothesis when the alternative is true.

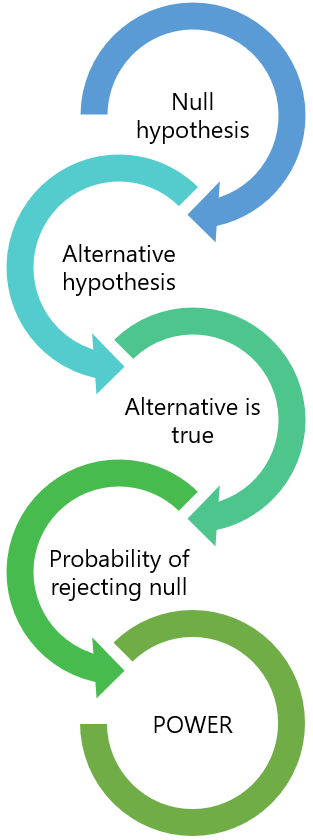
As we have explained above, interpreting a failure to reject the null hypothesis is not always straightforward. Instead, interpreting a rejection is somewhat easier.

When we reject the null, we know that the data has provided a lot of evidence against the null. In other words, it is unlikely (how unlikely depends on the size of the test) that the null is true given the data we have observed.

There is an important caveat though. The null hypothesis is often made up of several assumptions, including:

the main assumption (the one we are testing);

other assumptions (e.g., technical assumptions) that we need to make in order to set up the hypothesis test.

For instance, in Example 2 above (reliability of a production plant), the main assumption is that the expected number of production halts per year is equal to 1. But there is also a technical assumption: the number of production halts has a Poisson distribution.

It must be kept in mind that a rejection is always a joint rejection of the main assumption and all the other assumptions .

Therefore, we should always ask ourselves whether the null has been rejected because the main assumption is wrong or because the other assumptions are violated.

In the case of Example 2 above, is a rejection of the null due to the fact that the expected number of halts is greater than 1 or is it due to the fact that the distribution of the number of halts is very different from a Poisson distribution?

When we suspect that a rejection is due to the inappropriateness of some technical assumption (e.g., assuming a Poisson distribution in the example), we say that the rejection could be due to misspecification of the model .

The right thing to do when these kind of suspicions arise is to conduct so-called robustness checks , that is, to change the technical assumptions and carry out the test again.

In our example, we could re-run the test by assuming a different probability distribution for the number of halts (e.g., a negative binomial or a compound Poisson - do not worry if you have never heard about these distributions).

If we keep obtaining a rejection of the null even after changing the technical assumptions several times, the we say that our rejection is robust to several different specifications of the model .

Even if the null hypothesis is true, a wrong technical assumption can lead to reject the null too often.

What are the main practical implications of everything we have said thus far? How does the theory above help us to set up and test a null hypothesis?

What we said can be summarized in the following guiding principles:

A test of hypothesis is like a criminal trial and you are the prosecutor . You want to find evidence that the defendant (the null hypothesis) is guilty. Your job is not to prove that the defendant is innocent. If you find yourself hoping that the defendant is found not guilty (i.e., the null is not rejected) then something is wrong with the way you set up the test. Remember: you are the prosecutor.

Compute the power of your test against one or more relevant alternative hypotheses. Do not run a test if you know ex-ante that it is unlikely to reject the null when the alternative hypothesis is true.

Beware of technical assumptions that you add to the main assumption you want to test. Make robustness checks in order to verify that the outcome of the test is not biased by model misspecification.

$H_{0}$

More examples of null hypotheses and how to test them can be found in the following lectures.

Where the example is found	Null hypothesis
	The mean of a normal distribution is equal to a certain value
	The variance of a normal distribution is equal to a certain value
	A vector of parameters estimated by MLE satisfies a set of linear or non-linear restrictions
	A regression coefficient is equal to a certain value

The lecture on Hypothesis testing provides a more detailed mathematical treatment of null hypotheses and how they are tested.

This lecture on the null hypothesis was featured in Stanford University's Best practices in science .

Stanford University Best Practices in Science.

Previous entry: Normal equations

Next entry: Parameter

How to cite

Please cite as:

Taboga, Marco (2021). "Null hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/null-hypothesis.

Most of the learning materials found on this website are now available in a traditional textbook format.

Permutations
Characteristic function
Almost sure convergence
Likelihood ratio test
Uniform distribution
Bernoulli distribution
Multivariate normal distribution
Chi-square distribution
Maximum likelihood
Mathematical tools
Fundamentals of probability
Probability distributions
Asymptotic theory
Fundamentals of statistics
About Statlect
Cookies, privacy and terms of use
Precision matrix
Distribution function
Mean squared error
IID sequence
To enhance your privacy,
we removed the social buttons,
but don't forget to share .

Null Hypothesis Examples

ThoughtCo / Hilary Allison

Scientific Method
Chemical Laws
Periodic Table
Projects & Experiments
Biochemistry
Physical Chemistry
Medical Chemistry
Chemistry In Everyday Life
Famous Chemists
Activities for Kids
Abbreviations & Acronyms
Weather & Climate
Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as H 0 (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.


Are teens better at math than adults?	Age has no effect on mathematical ability.
Does taking aspirin every day reduce the chance of having a heart attack?	Taking aspirin daily does not affect heart attack risk.
Do teens use cell phones to access the internet more than adults?	Age has no effect on how cell phones are used for internet access.
Do cats care about the color of their food?	Cats express no food preference based on color.
Does chewing willow bark relieve pain?	There is no difference in pain relief after chewing willow bark versus taking a placebo.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
What Are Examples of a Hypothesis?
Random Error vs. Systematic Error
Six Steps of the Scientific Method
What Is a Hypothesis? (Science)
Scientific Method Flow Chart
What Are the Elements of a Good Hypothesis?
Scientific Method Vocabulary Terms
Understanding Simple vs Controlled Experiments
The Role of a Controlled Variable in an Experiment
What Is an Experimental Constant?
What Is a Testable Hypothesis?
Scientific Hypothesis Examples
What Is the Difference Between a Control Variable and Control Group?
DRY MIX Experiment Variables Acronym
What Is a Controlled Experiment?
Scientific Variable

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

Research Question	Null Hypothesis
Do teenagers use cell phones more than adults?	Teenagers and adults use cell phones the same amount.
Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil?	Tomato plants show no difference in growth rates when planted in compost rather than soil.
Does daily meditation decrease the incidence of depression?	Daily meditation does not decrease the incidence of depression.
Does daily exercise increase test performance?	There is no relationship between daily exercise time and test performance.
Does the new vaccine prevent infections?	The vaccine does not affect the infection rate.
Does flossing your teeth affect the number of cavities?	Flossing your teeth has no effect on the number of cavities.

When Do We Reject The Null Hypothesis?

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Probability and statistical significance in ab testing. Statistical significance in a b experiments

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.

Purpose of a Null Hypothesis

The primary purpose of the null hypothesis is to disprove an assumption.
Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.

Data Science
Data Analysis
Data Visualization
Machine Learning
Deep Learning
Computer Vision
Artificial Intelligence
AI ML DS Interview Series
AI ML DS Projects series
Data Engineering
Web Scrapping

Understanding Hypothesis Testing

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.

To test the validity of the claim or assumption about the population parameter:

A sample is drawn from the population and analyzed.
The results of the analysis are used to decide whether the claim is true or not.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis. Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.

Key Terms of Hypothesis Testing

Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 : [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]

To delve deeper into differences into both types of test: Refer to link

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).

	Null Hypothesis is True	Null Hypothesis is False
Null Hypothesis is True (Accept)	Correct Decision	Type II Error (False Negative)
Alternative Hypothesis is True (Reject)	Type I Error (False Positive)	Correct Decision

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ), suggesting an effect or difference.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

If Test Statistic>Critical Value: Reject the null hypothesis.
If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]

[Tex]\bar{x} [/Tex] is the sample mean,
μ represents the population mean,
σ is the standard deviation
and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]

t = t-score,
x̄ = sample mean
μ = population mean,
s = standard deviation of the sample,
n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]

[Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
i,j are the rows and columns index respectively.
[Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]

Real life Examples of Hypothesis Testing

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

m = mean of the difference i.e X after, X before
s = standard deviation of the difference (d) i.e d i = X after, i − X before,
n = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Case A

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

import numpy as np from scipy import stats # Data before_treatment = np . array ([ 120 , 122 , 118 , 130 , 125 , 128 , 115 , 121 , 123 , 119 ]) after_treatment = np . array ([ 115 , 120 , 112 , 128 , 122 , 125 , 110 , 117 , 119 , 114 ]) # Step 1: Null and Alternate Hypotheses # Null Hypothesis: The new drug has no effect on blood pressure. # Alternate Hypothesis: The new drug has an effect on blood pressure. null_hypothesis = "The new drug has no effect on blood pressure." alternate_hypothesis = "The new drug has an effect on blood pressure." # Step 2: Significance Level alpha = 0.05 # Step 3: Paired T-test t_statistic , p_value = stats . ttest_rel ( after_treatment , before_treatment ) # Step 4: Calculate T-statistic manually m = np . mean ( after_treatment - before_treatment ) s = np . std ( after_treatment - before_treatment , ddof = 1 ) # using ddof=1 for sample standard deviation n = len ( before_treatment ) t_statistic_manual = m / ( s / np . sqrt ( n )) # Step 5: Decision if p_value <= alpha : decision = "Reject" else : decision = "Fail to reject" # Conclusion if decision == "Reject" : conclusion = "There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different." else : conclusion = "There is insufficient evidence to claim a significant difference in average blood pressure before and after treatment with the new drug." # Display results print ( "T-statistic (from scipy):" , t_statistic ) print ( "P-value (from scipy):" , p_value ) print ( "T-statistic (calculated manually):" , t_statistic_manual ) print ( f "Decision: { decision } the null hypothesis at alpha= { alpha } ." ) print ( "Conclusion:" , conclusion )

T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05.

The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] and we get accordingly , Z =2.039999999999992.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Python Implementation of Case B

import scipy.stats as stats import math import numpy as np # Given data sample_data = np . array ( [ 205 , 198 , 210 , 190 , 215 , 205 , 200 , 192 , 198 , 205 , 198 , 202 , 208 , 200 , 205 , 198 , 205 , 210 , 192 , 205 , 198 , 205 , 210 , 192 , 205 ]) population_std_dev = 5 population_mean = 200 sample_size = len ( sample_data ) # Step 1: Define the Hypotheses # Null Hypothesis (H0): The average cholesterol level in a population is 200 mg/dL. # Alternate Hypothesis (H1): The average cholesterol level in a population is different from 200 mg/dL. # Step 2: Define the Significance Level alpha = 0.05 # Two-tailed test # Critical values for a significance level of 0.05 (two-tailed) critical_value_left = stats . norm . ppf ( alpha / 2 ) critical_value_right = - critical_value_left # Step 3: Compute the test statistic sample_mean = sample_data . mean () z_score = ( sample_mean - population_mean ) / \ ( population_std_dev / math . sqrt ( sample_size )) # Step 4: Result # Check if the absolute value of the test statistic is greater than the critical values if abs ( z_score ) > max ( abs ( critical_value_left ), abs ( critical_value_right )): print ( "Reject the null hypothesis." ) print ( "There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL." ) else : print ( "Fail to reject the null hypothesis." ) print ( "There is not enough evidence to conclude that the average cholesterol level in the population is different from 200 mg/dL." )

Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.

Limitations of Hypothesis Testing

Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( [Tex]H_o [/Tex] ): No effect or difference exists. Alternative Hypothesis ( [Tex]H_1 [/Tex] ): An effect or difference exists. Significance Level ( [Tex]\alpha [/Tex] ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

10.2 - steps used in a hypothesis test.

Regardless of the type of hypothesis being considered, the process of carrying out a significance test is the same and relies on four basic steps:

State the null and alternative hypotheses (see section 10.1 ) Also think about the type 1 error (rejecting a true null) and type 2 error (declaring the plausibility of a false null) possibilities at this time and how serious each mistake would be in terms of the problem.

Collect and summarize the data so that a test statistic can be calculated. A test statistic is a summary of the data that measures the difference between what is seen in the data and what would be expected if the null hypothesis were true. It is typically standardized so that a p -value can be obtained from a reference distribution like the normal curve.

Use the test statistic to find the p -value. The p -value represents the likelihood of getting our test statistic or any test statistic more extreme if, in fact, the null hypothesis is true.

For a one-sided "greater than" alternative hypothesis, the "more extreme" part of the interpretation refers to test statistic values larger than the test statistic given.
For a one-sided "less than" alternative hypothesis, the "more extreme" part of the interpretation refers to test statistic values smaller than the test statistic given.
For a two-sided "not equal to" alternative hypothesis, the "more extreme" part of the interpretation refers to test statistic values that are farther away from the null hypothesis that the test statistic given at either the upper end or lower end of the reference distribution (both "tails").

Interpret what the p -value is telling you and make a decision using the p -value. Does the null hypothesis provide a reasonable explanation of the data or not? If not it is statistically significant and we have evidence favoring the alternative. State a conclusion in terms of the problem.

Common Decision Rules seen in the literature

If the p -value ≤ .05 , we often see scientists declare their data to be "significant."
If the p -value ≤ .01 , we often see scientists declare their data to be "highly significant".
If the p -value > .05 , we often see scientists declare their data to be "not significant".

Example 10.9: Left Handed Artists: (continuation of example 10.2) Section

About 10% of the human population is left-handed. A researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed that people in the general population. A random sample of 100 students in the College of Arts and Architecture is obtained and 18 of these students were found to be left-handed.

Research Question : Are artists more likely to be left-handed than people in the general population?

Null Hypothesis : Population proportion of left-handed students in the College of Art and Architecture = 0.10 ( p = 0.10).
Alternative Hypothesis : Population proportion of left-handed students in the College of Art and Architecture > 0.10 ( p > 0.10).

Now that you know the null and alternative hypothesis, did you think about what the type 1 and type 2 errors are? It is important to note that Step 1 is before we even collect data. Identifying these errors helps to improve the design of your research study. Let's write them out:

Type 1 error : Claim artists are more likely to be left-handed than people in the general population when in truth they are not more likely.
Type 2 error : Fail to claim artists are more likely to be left-handed than people in the general population when they are in fact more likely.

In this case, the consequences of these two errors are fairly similar (e.g. installing more or fewer left-handed desks in classrooms that are needed).

In the sample of 100 students listed above, the sample proportion is 18 / 100 = 0.18. The hypothesis test will determine whether or not the null hypothesis that p = 0.1 provides a plausible explanation for the data. If not we will see this as evidence that the proportion of left-handed Art & Architecture students is greater than 0.10.

If the null hypothesis is true then the standard error of the sample proportion would be $\sqrt{\frac{0.1(1-0.1)}{100}} = 0.03$ and the sample proportion would follow the normal curve. Thus, we can use the standard score z = (0.18-0.10) / 0.03 = 2.67 as our test statistic.

Using the normal curve table for the Z -value of 2.67 we find the p -value to be about 0.004. Notice that the one-sided alternative hypothesis says to watch out for large values so we look at the percentage of the normal curve above 2.67 to get the p -value.

Interpretation of the p -value. The likelihood of getting our test statistic of 2.67 or any higher value, if in fact, the null hypothesis is true, is 0.004.

Since the p -value of 0.004 is so small, the null hypothesis provides a very poor explanation of the data. We find good evidence that the population proportion of left-handed students in the College of Art and Architecture exceeds 0.10.

Now that we have made our decision, we are only at risk of making a type 1 error. It is not possible at this point to make a type 2 error because we rejected the null hypothesis.

Example 10.10: The Weight of McDonald's French Fries in Japan Section

After receiving complaints from McDonald's customers in Japan about the amount of french fries being served, the online news magazine "Rocket News" decided to test the actual of the fries served at a particular Japanese McDonald's restaurant. According to the Rocket News article, the official weight standard set by McDonald's of Japan is for a medium-sized fries to weigh 135 grams. The publication weighed the fries from ten different medium fries they purchased and found the average weight of the fries in their sample to be 130 grams with a standard deviation of 9 grams.

Research Question : Does the data suggest that the medium fries from this McDonald's in Japan are underpacked?

Null Hypothesis : Population mean weight of medium fries = 135 grams
Alternative Hypothesis : Population mean weight of medium fries < 135 grams

The sample mean weight was 130 grams. Also, the sample standard deviation was 9 grams so the standard error of the mean is found to be $\frac{9}{\sqrt{10}} = 2.85$ grams. The test statistic would be the standardized value (130-135) / 2.85 = -1.76.

Since the sample size is only 10, the sample standard deviation would be an unreliable estimate of the population standard deviation so the normal curve would not be appropriate to use as the reference distribution to find the p -value. In this case, the t curve would be used instead and it turns out that the percentage of a t -curve below -1.76 when you have a sample size of 10 is about 6%.

Interpretation of the p -value. The likelihood of getting our test statistic of -1.76 or any smaller value, if in fact, the null hypothesis is true, is about 6%.

Since the p -value is around 6% we are near the border of what people often use as a cutoff for declaring a significant result. Given the amount of variability from one package of fries to the next, there is a reasonable chance that we would see a sample average like this even if the restaurant met the official standard weight on average.

It is important to remember in carrying out the mechanics of a significance test that you are only doing a probability calculation assuming the null hypothesis is true . Because the calculation is done under that assumption, it cannot say anything about the chances that the null hypothesis or the alternative hypothesis are true.

Pardon Our Interruption

As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:

You've disabled JavaScript in your web browser.
You're a power user moving through this website with super-human speed.
You've disabled cookies in your web browser.
A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .

To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

Recommended

How physicians can fix media bias with science

The assassination attempt is the straw that breaks the camel’s back. The “gaslighting” is over. The rules for truth by legacy media are never examined for objectivity. We do not have the Inquisition in the United States; we have the legacy media.

One “fact-checker” measures truth by “Pinocchios.” There is a better way—hypothesis testing. Who better to know about hypothesis testing than a physician?

What if the facts about how Medicare is represented by two media outlets are tested? Hypothesis testing follows four rules:

1. Identify the truth: The truth is out there. Truth-telling has nine phases, each representing a specific duty that pertains to an ideal storyteller.

The initiation phase: The duty to collect all the facts.
The acceptance phase: The duty to accept a fact verifiable by objective evidence.
The rejection phase: The duty to reject an artifact not verifiable by objective evidence.
The attribution phase: The duty to source the facts.
The external review phase: The duty to examine the motives of others to influence facts.
The internal review phase: The duty to examine a personal motive to influence facts.
The discrimination phase: The duty to distinguish an opinion from a fact. Opinions, even a consensus by authorities, are not facts.
The equanimity phase: The duty not to contaminate a fact with emotion.
The analysis phase: The duty to use facts, and only facts, to arrive at a conclusion.

2. State the subject matter: It is the actual storyteller’s version of reality. The subject matter contains the same facts, but some may be subtly misrepresented, just enough to satisfy the conclusion. The subject matter is divided into the same nine phases as they pertain to the actual storyteller.

3. The Test: Each phase of the subject matter is compared to its counterpart in the truth. The comparison measures the “relative risk” resulting from the misrepresentation of a fact by the actual storyteller.

If there is no difference, the relative risk equals 1.0.
If there is a difference, the relative risk is greater than 1.0. A relative risk greater than 1.0 is a Risk of Bias. For the sake of transparency, the assignments of Risk of Bias are documented for anyone to see and, if need be, to dispute.

A single sample of nine relative risks emerges representing each phase in the subject matter. Some are 1.0, and some are greater than 1.0. Because storytellers naturally tend to exaggerate a fact, producing a relative risk greater than 1.0, this discrepancy itself is not proof of a departure from the truth. Bias is intentional. For proof, the collective difference among the nine relative risks in all phases of the subject matter must be statistically significant.

4. Analysis: To determine a statistically significant difference, the sample is analyzed using the single-sample T-test, found in any statistical software. The level of significance, or alpha, is 0.05, which corresponds to 95 percent confidence. The population mean, or mu, is 1.0, which corresponds to the truth. The result is the p-value.

If the p-value is equal to or greater than 0.05, there is no statistically significant difference between the subject matter and the truth. Although there may be a phase that contains an exaggeration, the risk of bias is not sufficient for it to misrepresent reality. Therefore, there is no bias. This is the null hypothesis. If the null hypothesis is retained, the subject matter is the null hypothesis.
If the p-value is less than 0.05, there is a statistically significant difference. Therefore, there is quantifiable proof of bias. This is the alternate hypothesis. The alternate hypothesis is accepted by default. If the null hypothesis is rejected, the subject matter is the alternate hypothesis.

Hypothesis testing, unlike “Pinocchios,” objectively makes a valid comparison between truth and facsimile. A Pinocchio, while quantitative, has no level of confidence. However, a p-value has a level of confidence of 95 percent. For a rational person, 95 percent confidence stands in stark contrast to a Pinocchio.

As an example of hypothesis testing, the truth consists of the verifiable facts about Medicare that are publicly available in government documents. The subject matter consists of two media outlets’ versions of the truth.

One storyteller is Fox News. The sample is 1.0, 1.0, 1.0, 1.0, 1.0, 1.5, 1.5, 2.0, 1.0, and the p-value is 0.051893. The collective risk of bias is not sufficient to misrepresent reality.

The other storyteller is MSNBC. The sample is 1.5, 1.5, 1.5, 2.0, 1.5, 1.5, 1.5, 2.0, 2.0, and the p-value is 0.000022. The collective risk of bias is sufficient to misrepresent reality.

The difference between the two p-values shows that MSNBC’s version of Medicare is 99.9 percent less reliable than Fox’s version.

Howard Smith is an obstetrics-gynecology physician.

Why I won't let my wife see her EOBs anymore

How compassionate communities can transform the lives of schizophrenia patients

Tagged as: Mainstream media

More by Howard Smith, MD

The truth about medical lawsuits: What the numbers reveal

The flaw with medical malpractice litigation, why most medical malpractice claims never see a courtroom, related posts.

Social media: Striking a balance for physicians and parents

I was trolled by another physician on social media. I am happy I did not respond.

Are negative news cycles and social media injurious to our health?

How I used social media to get promoted to professor

Sharing mental health issues on social media

How physicians can engage on social media

Changing the narrative: medicine and resilience in Israel

A strategic approach for leveraging Lyapunov functions in health care artificial intelligence

How these doctors overcame ethnic conflict to unite in medicine

How a doctor transformed grief into personal growth

How embracing vulnerability transforms pain into power

A life of purpose: free from societal pressures that lead us astray

How medical school curricula perpetuate inequality

President Biden: a closer look at leadership, dignity, and aging

Closing the colorectal cancer screening gap: the need for clear guidance on the use of new screening options

Balancing values and metrics: the modern physician’s dilemma [PODCAST]

The hidden connection between dementia and PTSD

Past 6 months.

A doctor’s eye-opening journey as a patient

The truth behind opioid use disorder

From conviction to appeal: a doctor’s opioid case sparks debate

The sham peer review: a hidden contributor to the doctor shortage

The unseen dangers of faulty expert witness testimony

Creating a subspecialty track for experienced hospitalists

Is skin really the largest organ? The truth might surprise you.

Latest advancements in inflatable penile implants: a men’s health urologist’s perspective

A medical student’s transformative encounter with end-of-life care [PODCAST]

Subscribe to KevinMD and never miss a story!

Get free updates delivered free to your inbox.

Find jobs at Careers by KevinMD.com

Search thousands of physician, PA, NP, and CRNA jobs now.

CME Spotlights

Comments are moderated before they are published. Please read the comment policy .

Troubleshooting High CPU Utilization in SQL Server

By: Jeffrey Yao | Updated: 2024-08-19 | Comments | Related: > Monitoring

In a database environment, you may find slow SQL Server performance due to high CPU usage. Quite often, this slowness is caused by one or a few SQL Server sessions using high CPU resources, and such queries can even cause the server's CPU to reach 100% for a long period.

As a DBA, how can you proactively monitor high CPU usage by the SQL Server instance and find out which sessions are the culprits for such high CPU?

When a server machine running SQL Server has high CPU, there are two scenarios causing the issue:

SQL Server service, or
Other applications, such as virus scan applications, are installed on the machine.

From a DBA perspective, I am interested in scenario 1, i.e., high CPU caused by the SQL Server service and the "offending" SQL sessions that use high CPU resources.

So, here is my solution for CPU monitoring and session loggings:

Run PowerShell cmdlet get-counter to get the counters ( \PROCESS(_TOTAL)\% Processor Time ) and ( \PROCESS(SQLSERVER)\% Processor Time ) on the target servers and save the collected result into a central table.
When the SQL Server process CPU value exceeds a predefined threshold [X]%, we will go to the next step. I usually choose X = 85, i.e., the SQL instance process is using more than 85% of the total CPU.
Run sp_whoisactive on the target SQL Server instance and export the result to another central repository table.
Send a notification email to the DBA team about the high CPU issue and the corresponding SQL queries collected from the previous step.

To implement the solution, we will first perform the following setup.

All the monitoring work will be set up on a central monitoring server, which has PowerShell V5.1+ and SQL Server PowerShell module installed, together with an SQL Server instance installed (can be a free Express edition). Database mail needs to be set up as well to get notifications.

Source Code

We will first create two tables: one to store the get-counter result and another to store the sp_whoisactive result.

We need to create a monitoring PowerShell script to monitor the CPUs of our designated target servers. The monitoring script will do three things:

Keep collecting CPU counter values via get-counter and populating the dbo.CPUCounter table.
After each data collection, analyze whether the CPU is above a predefined threshold on some monitored servers.
If the CPU usage exceeds the predefined threshold, run sp_whoisactive on those servers, save the results to dbo.WhoisactiveResult, and send an email alert to the DBA team.

The following script makes a few assumptions:

PowerShell V5.1 or higher and sqlserver module are installed on the monitoring server, which can connect to all the monitored servers.
On the monitored server, we have a SQL Server instance installed, and the database mail is set up as well.
Sp_whoisactive v12.00 is installed on the monitored servers.
For simplicity, we assume only default SQL Server instances, i.e., not named instances, are installed on the monitored servers.

We first create the PowerShell script shown below.

If I run the PowerShell script, I can see the CPU performance data is collected in the table dbo.CPUCounter .

CPU performance data collected in the table dbo.CPUCounter

If we want to send an alert if the SQL Server service CPU is more than 85% within the last 5 minutes (assuming we collect CPU counters every minute), we need to calculate the average CPU usage by the SQL Server for the last 5 minutes. If it exceeds the defined threshold, we will send an alert via database mail.

We need to expand the previous PowerShell code to include the logic to find whether the threshold is reached on which server instances and then send an alert email if true.

We can put the whole PowerShell script into a SQL job on the center server, as shown below.

Note: My central server is SQL Server 2019 standard edition, and the key point is in the first line of the PowerShell script. It should be #NOSQLPS to avoid loading the default SQLPS module. Please see the reference link below for details.

To test the script, we can purposely set a low threshold value:

We also need to give the correct computer names for $svr_list:

For each server, please make sure that the CPU performance counter can be collected from the central server by running the following quick PowerShell cmdlet:

I have scheduled the job to run every minute, and here is the sample alert email I received when the CPU of the SQL Server process on one or more monitored servers exceeded the predefined threshold, which is 15% (for test purposes).

I can copy and paste the SELECT query in the alert email and run it against the central server, and the result is as follows. The key point to check the query result is column [CPU_delta], which is automatically calculated by sp_whoisactive between 2 seconds. This is done by providing @delta_interval = 2 parameter to sp_whoisactive (which you can see in the code above). Of course, we can change the value of @delta_interval to meet our own needs.

This tip describes a simple, near real-time monitoring of the SQL Server process CPU usage and the queries running at the time of high CPU.

Since the monitoring is based on the CPU usage of each process, it minimizes the potential false alarms about the SQL Server process as a culprit for high CPU usage. If high CPU usage is caused by another process other than the SQL Server process, this monitoring will not send an alert to the DBA team.

This framework can be extended to monitor other SQL Server performance issues. For example, if the tempdb data file keeps expanding or a database log file keeps growing, we DBAs may want to determine which queries could be the culprits for such issues. We can monitor the default SQL trace file, find the data file or log file expanding events, and then run the sp_whoisactive on the target server to capture the current query running status.

Run PowerShell from SQL Server Agent
Sp_whoisactive documentation
Using the SQL Server Default Trace to Audit Events

SQL Server High CPU Query Use Monitoring with PowerShell

About the author

Comments For This Article

COMMENTS

16.3: The Process of Null Hypothesis Testing
We can break the process of null hypothesis testing down into a number of steps: Formulate a hypothesis that embodies our prediction ( before seeing the data) Collect some data relevant to the hypothesis. Specify null and alternative hypotheses. Fit a model to the data that represents the alternative hypothesis and compute a test statistic.
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
Null Hypothesis: Definition, Rejecting & Examples
In a hypothesis test, this process involves comparing the p-value to your significance level. Rejecting the Null Hypothesis. Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. ... Null Hypothesis ...
1.2: The 7-Step Process of Statistical Hypothesis Testing
Step 7: Based on steps 5 and 6, draw a conclusion about H0. If the F\calculated F \calculated from the data is larger than the Fα F α, then you are in the rejection region and you can reject the null hypothesis with (1 − α) ( 1 − α) level of confidence. Note that modern statistical software condenses steps 6 and 7 by providing a p p -value.
Null hypothesis
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...
9.1: Introduction to Hypothesis Testing
In hypothesis testing, the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis.The null hypothesis is usually denoted $H_0$ while the alternative hypothesis is usually denoted $H_1$. An hypothesis test is a statistical decision; the conclusion will either be to reject the null hypothesis in favor ...
6a.2
Below these are summarized into six such steps to conducting a test of a hypothesis. Set up the hypotheses and check conditions: Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as H 0, which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is ...
13.1 Understanding Null Hypothesis Testing
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that ...
Understanding Null Hypothesis Testing
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
Statistical hypothesis test
A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently supports a particular hypothesis. ... An example of Neyman-Pearson hypothesis testing (or null hypothesis statistical significance testing) can be made by a change to the radioactive suitcase example. ...
11.2.1
Step 1: Check assumptions and write hypotheses. When conducting a chi-square goodness-of-fit test, it makes the most sense to write the hypotheses first. The hypotheses will depend on the research question. The null hypothesis will always contain the equalities and the alternative hypothesis will be that at least one population proportion is ...
Understanding Statistical Testing
Steps in the Application of the Logic of Statistical Testing. Step 1. Determine the hypothesis-specific partition of the parameter space associated with the data generating process. How this is achieved depends on the substance and logic of the research being pursued and is not merely a question of statistics. Step 2.
Null hypothesis significance testing: a short tutorial
Fisher, significance testing, and the p-value. The method developed by ( Fisher, 1934; Fisher, 1955; Fisher, 1959) allows to compute the probability of observing a result at least as extreme as a test statistic (e.g. t value), assuming the null hypothesis of no effect is true.This probability or p-value reflects (1) the conditional probability of achieving the observed outcome or larger: p(Obs ...
1.2
Step 7: Based on Steps 5 and 6, draw a conclusion about H 0. If F calculated is larger than F α, then you are in the rejection region and you can reject the null hypothesis with ( 1 − α) level of confidence. Note that modern statistical software condenses Steps 6 and 7 by providing a p -value. The p -value here is the probability of getting ...
Null hypothesis
The null is like the defendant in a criminal trial. Formulating null hypotheses and subjecting them to statistical testing is one of the workhorses of the scientific method. Scientists in all fields make conjectures about the phenomena they study, translate them into null hypotheses and gather data to test them.
8.6: Steps of the Hypothesis Testing Process
The process of testing hypotheses follows a simple four-step procedure. This process will be what we use for the remainder of the textbook and course, and though the hypothesis and statistics we use will change, this process will not. Step 1: State the Hypotheses. Your hypotheses are the first thing you need to lay out.
How to Formulate a Null Hypothesis (With Examples)
To distinguish it from other hypotheses, the null hypothesis is written as H 0 (which is read as "H-nought," "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the ...
What Is The Null Hypothesis & When To Reject It
Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. ... R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods, 5(2), 241. Rozeboom, W. W. (1960). The ...
PDF Null Hypothesis Significance Testing
Joachim Krueger Brown University Null hypothesis significance testing (NHST) is the re- searcher's workhorse for making inductive inferences. This method has often been challenged, has ...
Null Hypothesis
The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null ...
Understanding Hypothesis Testing
Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. ... Critical value: The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a ...
10.2
Step 1: State Null and Alternative Hypotheses. Null Hypothesis: Population mean weight of medium fries = 135 grams. Alternative Hypothesis: Population mean weight of medium fries < 135 grams. Step 2: Collect and summarize the data so that a test statistic can be calculated. The sample mean weight was 130 grams.
7.6: Steps of the Hypothesis Testing Process
Taft College. The process of testing hypotheses follows a simple four-step procedure. This process will be what we use for the remained of the textbook and course, and though the hypothesis and statistics we use will change, this process will not. Step 1: State the Hypotheses. Your hypotheses are the first thing you need to lay out.
Mastering Hypothesis Testing: 8 Steps Decoded
Deliverable 04 Worksheet 1. Describe the 8 steps in the process for hypothesis testing. Explain the decision criteria for rejecting the null hypothesis for both the p-value method and the critical value method. Answer and Explanation: The remaining problems refer to the following scenario: A claim is made that the average salary for all jobs in Minnesota is less than $75,000.
How physicians can fix media bias with science
Therefore, there is quantifiable proof of bias. This is the alternate hypothesis. The alternate hypothesis is accepted by default. If the null hypothesis is rejected, the subject matter is the alternate hypothesis. Hypothesis testing, unlike "Pinocchios," objectively makes a valid comparison between truth and facsimile.
Troubleshooting High CPU Utilization in SQL Server
Problem. In a database environment, you may find slow SQL Server performance due to high CPU usage. Quite often, this slowness is caused by one or a few SQL Server sessions using high CPU resources, and such queries can even cause the server's CPU to reach 100% for a long period.
Get Docker
Download and install Docker on the platform of your choice, including Mac, Linux, or Windows.

Have a language expert improve your writing

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Table of contents

Here's why students love Scribbr's proofreading services

Cite this Scribbr article

Is this article helpful?

Rebecca Bevans

Null Hypothesis: Definition, Rejecting & Examples

What is a Null Hypothesis?

Null Hypothesis Examples

When to Reject the Null Hypothesis

Rejecting the Null Hypothesis

Failing to Reject the Null Hypothesis

How to Write a Null Hypothesis

Group Means

Group Proportions

Correlation and Regression Coefficients

Share this:

Reader Interactions

Comments and Questions Cancel reply

13.1 Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Key Takeaways

Share This Book

Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Long Descriptions

Media Attributions

Share This Book

Null hypothesis significance testing: a short tutorial

Version Changes

Peer Review Summary

The Null Hypothesis Significance Testing framework

Fisher, significance testing, and the p-value

What is not a p-value? Common mistakes

Neyman-Pearson, hypothesis testing, and the α-value

Acceptance or rejection of H0?

Confidence intervals

The (correct) use of NHST

What to report and how?

Funding Statement

Referee response for version 3

Stephen J. Senn

Referee response for version 2

Referee response for version 1

Daniel Lakens

The null is like the defendant in a criminal trial

How to cite

Null Hypothesis Examples

What Is the Null Hypothesis?

Examples of the Null Hypothesis

Other Types of Hypotheses

Key Takeaways

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

How to Write a Null Hypothesis

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

Examples of Null Hypotheses

When Do We Reject The Null Hypothesis?

Why Do We Never Accept The Null Hypothesis?

Why Do We Use The Null Hypothesis?

Purpose of a Null Hypothesis

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

What is the difference between a null hypothesis and an alternative hypothesis?

What are some problems with the null hypothesis?

Why can a null hypothesis not be accepted?

Is a null hypothesis directional or non-directional?

Understanding Hypothesis Testing

What is Hypothesis Testing?

Defining Hypotheses

Key Terms of Hypothesis Testing

Why do we use Hypothesis Testing?

One-Tailed and Two-Tailed Test

One-Tailed Test