Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.

Understanding the concept of “truth assignment”.
Working on the book: Derek Goldrei. " Propositional and Predicate Calculus " (p. 40)
The author briefly introduces the concept of a function v :
We talked informally about knowing whether, in a particular set of circumstances, each propositional variable is true or false. More formally and elegantly, thsi set of circumstances is a function $v \colon P \to \{T,F\}$ , where $P$ is the set of propositional variables in our language.
Before introducing the concept of truth assignment , explains:
Let $Form(P, S)$ be the set of all formulas built up from propositional variables in a set $P$ using connectives in a set $S$ which includes $\land$ . We shall say that a function $v \colon Form(P,S) \to \{T,F\}$ respects the truth table $\land$ if $$ v((\theta \land \psi))= \begin{cases} T, &\text{if } v(\theta))=v(\psi)=T\\ F, &otherwise, \\ \end{cases} $$ for all formulas $\theta, \psi \in Form(P,S)$ .
I see how function $v$ respects the truth table of $\land$ . My question is:
- In which way are the truth value of $v(\theta)$ and $v(\psi)$ determined in that piecewise function ?
- What is the criteria for deciding whether $v(\theta)$ (or any propositional variable) is going to be $T$ or $F$ ?
- propositional-calculus
- $\begingroup$ See van Dalen , page 17 for the definition and the basic result: "If a valuation is only given for atoms then it is, by virtue of the definition by recursion [see your previous post], possible to extend it to all propositions. " $\endgroup$ – Mauro ALLEGRANZA Commented Oct 8, 2020 at 6:40
- $\begingroup$ Thank you so much, @Mauro ALLEGRANZA. That's exactly what I do not understand. Could you explain a little bit ? What does "...possible to extend it to all propositions", mean ? I see how the value of compound formulas is computes; I just do not see it when it comes to atoms. I mean, what determines the assignment of T or F to an atomic formula. $\endgroup$ – F. Zer Commented Oct 8, 2020 at 12:05
- $\begingroup$ Thank for the offering. I will appreciate if you could clarify the meaning of "...possible to extend it to all propositions". Also, is perhaps the assignment to atoms random ? I feel this is not really complicated but a detail evades me. $\endgroup$ – F. Zer Commented Oct 8, 2020 at 12:32
3 Answers 3
Ultimately the truth value $v(\varphi)$ of any formula $\varphi$ is determined by the truth values that $v$ assigns to the propositional variable appearing in $\varphi$ . Consider, for instance the following formula $\varphi$ :
$$(p\land\neg q)\lor(r\land q)\to p$$
If $v(p)=F$ , $v(q)=T$ , and $v(r)=F$ , then:
- $v(\neg q)$ must be $F$ in order to respect to truth table for $\neg$ ;
- $v(p\land\neg q)$ must then also be $F$ in order to respect the truth table for $\land$ ;
- $v(r\land q)$ must be $F$ for the same reason;
- $v\big((p\land\neg q)\lor(r\land q)\big)$ must be $F$ in order to respect the truth table for $\lor$ ; and finally
- $v(\varphi)$ must be $T$ in order to respect the truth table for $\to$ .
If we change the truth value of $r$ by setting $v(r)=T$ , we must then have $v(r\land q)=T$ , $v\big((p\land\neg q)\lor(r\land q)\big)=T$ , and $v(\varphi)=F$ .
In practice truth assignments are very often presented in the form of tables showing the truth values assigned to a particular formula under all possible assignments of truth values to its propositional variables. In this case we’d have the following table, and we could read off that $v(\varphi)=T$ for all truth assignments to $p,q$ , and $r$ except the one mentioned immediately above, the one in the fifth line of the table:
$$\begin{array}{c|c|c} p&q&r&p\land\neg q&r\land q&(p\land\neg q)\lor(r\land q)&\varphi\\\hline T&T&T&F&T&T&T\\ T&T&F&F&F&F&T\\ T&F&T&T&F&T&T\\ T&F&F&T&F&T&T\\ F&T&T&F&T&T&F\\ F&T&F&F&F&F&T\\ F&F&T&F&F&F&T\\ F&F&F&F&F&F&T \end{array}$$
- $\begingroup$ Very clear. Thank you so much, @Brian M. Scott ! I see what you explain about respecting the truth table of logical connectives. But, in which way the value of $v(\theta)$ is determined ($\theta$ being an atomic proposition) ? $\endgroup$ – F. Zer Commented Oct 8, 2020 at 11:59
- $\begingroup$ Taking a simple example, I know the value of $\sqrt{4}$ is going to be $2$, but in terms of truth assignments, I cannot see a predictable way of determining if a certain proposition is going to be true or false. $\endgroup$ – F. Zer Commented Oct 8, 2020 at 11:59
- $\begingroup$ Perhaps, there is a subtle point about functions that I'm not getting... $\endgroup$ – F. Zer Commented Oct 8, 2020 at 12:00
- $\begingroup$ @F.Zer: I’m not quite sure what you’re asking. Are you asking how, if $p$ is a propositional variable, one determines the truth value of $p$? That’s not a question with which propositional logic deals: propositional logic deals with how truth values of propositions are correctly combined. $\endgroup$ – Brian M. Scott Commented Oct 8, 2020 at 16:27
- 1 $\begingroup$ @F.Zer: Yes, that’s correct. For instance, the truth table in my answer shows every one of the $8$ possible truth assignments to the three variable $p,q$, and $r$, one per line. $\endgroup$ – Brian M. Scott Commented Oct 8, 2020 at 17:05
The above answers are thorough, but they overcomplicate matters by quite a bit by being too formal. A truth assignment ν is simply a row of values of atomic propositions in a truth table , nothing more, nothing less.
This row of atomic proposition values can be thought of as a function ν(φ) → {T, F} , which is true or T , if the value of the formula φ is true with that combination of values of atomic propositions ν and false or F, if the fomula φ is not true with said values. For example, if it is raining and cloudy or raining = T and cloudy = T , then
and the sequence raining cloudy = T T = ν for which ν(φ) = ν(raining ∧ cloudy) = T .
Another way of writing the fact that ν(φ) = T , or that φ is true with the observed combination of values of the atomic propositions, is ν ⊧ φ , or ν is a model of the formula φ . If φ is not true with the given combination of atomic proposition values ν , we say that ν ̸⊧ φ , or that ν is a counter model of φ .
Anyways, thinking about this in terms of truth tables is in my opinion more illustrative than most alternative presentations.
See Dirk van Dalen, Logic and Structure (5th ed., 2013) , page 17 for the definition and the basic result:
"If a valuation is only given for atoms then it is, by virtue of the definition by recursion, possible to extend it to all propositions."
What is a valuation ? Simply a function: $v : \text {PROP} \to \{ 0,1 \}$ ,
where [see page 7 ] $\text {PROP} = \{ p_0, p_1, \ldots \}$ is the collection of proposition symbols .
Side condition : van Dalen uses $\bot$ and consider it as a $0$ -ary connective. Thus, he needs the clause: for every valuation $v$ we must have: $v(\bot)=0$ .
Silly examples of valuations:
$v(p_i)=0$ , for every $i$ ; $v'(p_i)=1$ , for every $i$ .
Starting with an assignment $v$ , we can easily show how the truth tables for the basic connectives [see page 18 ] give us the recipe for computing the truth value for a formula $\varphi$ whatever.
Consider the formula $((p_0 ∧ p_1) → (\lnot p_0))$ [similar to the example used in your previous post ] and build the usual truth table:
$$\begin{array}{c|c|c} p_0&p_1&(p_0 \land p_1)&(\lnot p_0)&((p_0\land p_1)\to(\lnot p_0))&\\\hline 1&1&1&0&0\\ 1&0&0&0&1\\ 0&1&0&1&1\\ 0&0&0&1&1\\ \end{array}$$
Consider now the following valuation: $v(p_0)=0$ and $v(p_1)=1$ . It simply amounts to the third line in the table above.
Note : as we can imagine [but we can prove it: see Lemma 2.2.3 , page 18], what matters are only the value that the valuation assigns to the propositional symbols occurring into the formula.
The "recipe" is:
(i) $v(p_0)=0$ ; thus $v[(\lnot p_0)]=1$ .
(ii) $v(p_0)=0$ and $v(p_1)=1$ ; thus $v[(p_0 \land p_1)]=0$ .
(iii) $v[(p_0 \land p_1)]=0$ and $v[(\lnot p_0)]=1$ ; thus $v[((p_0 \land p_1)\to (\lnot p_0))]=1$ .
Note : in computing the truth value of the formula, we have followed the formation sequence [see Definition 2.1.4 , page 9] of the formula:
$p_0, p_1, (p_0 \land p_1), (\lnot p_0), ((p_0 \land p_1)\to (\lnot p_0))$ .
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged logic propositional-calculus ..
- Featured on Meta
- Bringing clarity to status tag usage on meta sites
- Join Stack Overflow’s CEO and me for the first Stack IRL Community Event in...
- 2024 Election Results: Congratulations to our new moderator!
Hot Network Questions
- Model reduction in linear regression by stepwise elimination of predictors with "non-significant" coefficients
- Why were there so many OSes that had the name "DOS" in them?
- Who was the French detective mentioned in Hitchcock's "Shadow of a Doubt"?
- The meaning of "sharp" in "sharp sweetness"
- Correct anonymization of submission using Latex
- Can we use "day and night time" instead of "day and night"?
- Humans are forbidden from using complex computers. But what defines a complex computer?
- What is the working justification of this circuit?
- Best memory / storage solution for high read / write throughput application(s)?
- What are the steps to write a book?
- Where Does Rashi Mention the Streets of Venice?
- Starting with 2014 "+" signs and 2015 "−" signs, you delete signs until one remains. What’s left?
- How resiliant is a private key passphase to brute force attacks?
- Children's book about intelligent bears or maybe cats
- Could they free up a docking port on ISS by undocking the emergency vehicle and letting it float next to the station for a little while
- Is the product of two NONZERO elements independently drawn from a prime field uniformly distributed?
- Remove spaces from the 3rd line onwards in a file on linux
- Canonical decomposition as wedge sum up to homotopy equivalence
- A probably Fantasy middle-length fiction about a probable vampire during the Blitz
- Consistency-proof of ZFC
- Engaging students in the beauty of mathematics
- package accents seems to be incompatible with Unicode-math
- Do images have propositional content?
- Can the Fourier transform of a test function vanish on an interval?
All Subjects
Truth Assignment
In thinking like a mathematician.
A truth assignment is a specific mapping of truth values to the variables in propositional logic. This means that each variable in a logical expression is assigned either 'true' or 'false', which allows us to determine the overall truth value of complex expressions built from those variables. Truth assignments are crucial in understanding how different combinations of truth values affect the validity of propositions and in constructing truth tables that systematically represent these relationships.
congrats on reading the definition of Truth Assignment . now let's actually learn it.
5 Must Know Facts For Your Next Test
- A truth assignment can be represented as a list where each variable is paired with its corresponding truth value, helping to analyze logical expressions.
- For a logical expression with 'n' variables, there are $2^n$ possible truth assignments, reflecting all combinations of true and false for those variables.
- Evaluating a logical expression under a specific truth assignment involves substituting the assigned values into the expression and calculating its resulting truth value.
- Truth assignments are essential for determining the satisfiability of propositional formulas, where a formula is satisfiable if there exists at least one truth assignment that makes it true.
- In constructing truth tables, each row corresponds to a unique truth assignment, allowing for a comprehensive evaluation of how different inputs affect the output of logical operations.
Review Questions
- A truth assignment functions by assigning true or false values to the variables in a propositional logic statement. This is important because it allows us to evaluate the overall truth value of complex logical expressions based on these individual assignments. By using different combinations of truth assignments, we can explore how these values impact the validity and satisfiability of various propositions.
- Truth assignments directly influence the construction of truth tables because each row in a table corresponds to a specific combination of truth values for the involved variables. As we fill out the table using all possible truth assignments, we can observe how each combination affects the outcome of logical expressions. This systematic representation aids in visualizing and analyzing the relationships between different propositions and their truth conditions.
- Understanding truth assignments significantly enhances problem-solving skills in propositional logic by providing a structured approach to evaluating logical statements. By knowing how to systematically apply different assignments, students can confidently tackle complex expressions and determine their validity. Additionally, mastering this concept allows for deeper insights into concepts like logical equivalence and contradictions, enabling students to approach problems with greater analytical skills and clarity.
Related terms
Propositional Logic : A branch of logic that deals with propositions and their relationships, focusing on how truth values can be assigned to statements that can be either true or false.
Logical Connectives : Symbols used in propositional logic to combine one or more propositions, such as AND, OR, and NOT, which influence the overall truth value of complex statements.
Truth Table : A systematic way of displaying all possible truth assignments for a given logical expression, showing how the truth values of its components lead to the overall truth value.
" Truth Assignment " also found in:
Subjects ( 6 ).
- Algebraic Logic
- Formal Logic I
- Formal Logic II
- Mathematical Logic
- Model Theory
- Proof Theory
© 2024 Fiveable Inc. All rights reserved.
Ap® and sat® are trademarks registered by the college board, which is not affiliated with, and does not endorse this website..
© Alexander Brandt 2023
Theme by the Executable Book Project
Propositional Logic
1.1. propositional logic #.
Propositional Logic is the logical system built around proposition s. From such propositions one can build logical arguments and implications.
In this section we will explore the language of propositions, their applications, and deriving logical equivalences.
The Language of Propositions
Propositions
Constructing Propositions
Connectives
Conjunction
Disjunction
Implication
Biconditional
Propositional Formulas
Truth Tables
Implication, Inverse, Converse, and Contrapositive
Applications
Translating English to Propositional Logic
Boolean Searches
Formal Specifications
Solving logic puzzles
Logical Equivalences
Logically Equivalent
Equivalence proof
Basic Propositions
1.1.1. The Language of Propositions #
Propositions are all about truth. Is a statement true or false? Is a statement correct or incorrect?
Propositions #
Definition (Proposition)
A proposition is a declarative sentence or statement has a truth value. It is a statement which is either true or false. Each proposition has a “truth value”: either true or false.
To get acquainted with propositions, let us see some examples and counterexamples.
Examples of propositions
Socrates was a human.
Socrates was a pigeon.
It is raining today.
The logo of Starbucks is a green mermaid.
\(1 + 1 = 2\)
\(1 + 1 = 4\)
Notice that propositions need not be a true statement. Propositions only need to be declarative . Their truth value may be true or false. However, all propositions must have a particular truth value. The statement cannot be both true and false. The statement must be able to be interpreted as true or false.
From the previous definition and examples, propositions are therefore not questions, general statements, demands, or hypotheses. Propositions do not have any variables, quantifiers, or parameters (e.g. the words “some” or “any” typically do not appear). Consider now a few non-examples.
Examples of statements that are not propositions
Do you have a dog?
Some coffee mug with a mermaid on it.
\(x + 2 = 3\)
\(y = x^2 - 1\)
Are each of these propositions?
I am a dolphin.
Supercalifragilisticexpialidocious.
Jupiter is the 5th planet from the sun.
On Thursdays, van Gogh painted landscapes.
\(\frac{11+56*3-8}{19} = 9\)
Yes. This is a statement which is false. The author and the reader are both humans, right?
No. A single adjective on its own can not be true or false.
Yes. This is a statement which is true.
Yes. While I do not personally know the truth value of this statement, it certainly has one.
Yes. A formula with no variables precisely stating an equality. The equality is true .
Constructing Propositions #
An entire proposition is often denoted by a single propositional variable . Propositional variables are typically among \(p, q, r, s, t, \ldots\) .
Using propositional variables
\(p := \) “The sky is blue”
\(q := \) “The sun rises from the west”
We also denote truth values in particular ways. “True” may be denoted by \(T\) . “False” may be denoted by \(F\) . When a proposition (or proposition variable) is known to always be true, we can replace it by \(T\) . When a proposition (or proposition variable) is known to always be false, we can replace it by \(F\) .
Connectives #
We can combine propositions (and propositional variables) into compound propositions or propositional formula s. This is akin to compound sentences and other logical connectives in natural language.
In propositional logic , we have 5 main connectives. Each connective has a corresponding meaning in natural language as we will soon see.
Negation: \(\neg\)
Conjunction: \(\land\)
Disjunction: \(\lor\)
Implication: \(\rightarrow\)
Biconditional: \(\leftrightarrow\)
Logical connectives are like arithmetic operators ( \(+, -, \times, \div\) ).
The negation of a proposition results in a proposition with the opposite truth value. It is akin to adding “not” into a sentence, or starting a sentence with “it is not that case that…”.
Given a proposition \(p\) its negation is \(\neg p\) and has the following truth values.
\(p\) | \(\neg p\) |
|---|---|
F |
|
T |
|
Let \(p := \) “the sky is blue”.
\(\neg p\) is “the sky is not blue” or “it is not the case that the sky is blue”.
Let \(q := \) “ \(2 + 2 = 5\) ”.
\(\neg q\) is “ \(2 + 2 \neq 5\) .
Notice in these examples that negation does not necessarily make a proposition false. Rather, it makes the proposition have the opposite truth value .
Conjunction #
The conjunction of two propositions is the logical “and” of the two propositions. The conjunction of two proposition is only true if both the propositions are individually true, otherwise the conjunction is false.
Given proposition \(p\) and \(q\) their conjunction is denoted \(p \land q\) and has the following truth values.
\(p\) | \(q\) | \(p \land q\) |
|---|---|---|
F | F |
|
F | T |
|
T | F |
|
T | T |
|
Let \(p\) be “birds lay eggs” and \(q\) be “my eyes are blue”. \(p \land q\) is then “birds lay eggs and my eyes are blue”.
Disjunction #
The disjunction of two propositions is the “or” of the two propositions. The disjunction is true if at least one of the propositions is individually true, otherwise the disjunction is false.
Given proposition \(p\) and \(q\) their disjunction is denoted \(p \lor q\) and has the following truth values.
\(p\) | \(q\) | \(p \lor q\) |
|---|---|---|
F | F |
|
F | T |
|
T | F |
|
T | T |
|
Let \(p\) be “it is raining” and \(q\) be “I am wearing sunglasses”. \(p \lor q\) is then “it is raining or I am wearing sunglasses”.
Notice that in this previous example, it is may be true that it is both raining and that I am wearing sunglasses. While that may be silly, \(p \lor q\) is still true! In logic, we only require that at least one of the propositions in a disjunction is true. That means both are allowed to simultaneously be true.
In natural language, “or” is often interpreted as an exclusive or .
Language “or”
“You can have a cookie or a piece of cake.” Most people assume that this means you can have a cookie or a piece of cake, but not both .
In logic, “or” is not exclusive. You can have a cookie, a piece of cake, or both !
If you want logical exclusive or, we use the symbol \(\oplus\) . However, we will not use that in this course.
What is the truth value of these compound propositions?
“The earth is round and the sky is blue.”
“Dogs or cats make great pets.”
“It is \(20^{\circ}\) Celsius outside and it is snowing.”
“Lemons are purple or grass is green”
True. Both propositions are individually true.
True. You may not like dogs, or you may not like cats, but at least one of dogs or cats make a great pet.
False. Both “it is \(20^{\circ}\) Celsius outside” and “it is snowing” cannot simultaneously be true. Therefore, their conjunction is false.
True. Lemons may not be purple, but (healthy) grass is green.
Implication #
Implication is one of the most challenging connectives to understand. Yet it is arguably the most important for creating logical arguments (see Logical Equivalences ).
An implication is a conditional statement . For two propositions \(p\) and \(q\) , \(p \rightarrow q\) is an implication which is read “if \(p\) , then \(q\) ”. You can also say “ \(p\) implies \(q\) ”.
Let \(p\) be “it is raining” and \(q\) be “the ground is wet”. \(p \rightarrow q\) can be read “if it is raining, then the ground is wet”.
In an implication \(p \rightarrow q\) , the first proposition \(p\) is known as the hypothesis , antecedent , or premise . The second proposition \(q\) is known as the conclusion or consequence .
Because an implication is a conditional , the truth value of the implication as a whole changes depending on the truth value of the premise. The following truth table summarizes the truth values of an implication.
\(p\) | \(q\) | \(p \rightarrow q\) |
|---|---|---|
F | F |
|
F | T |
|
T | F |
|
T | T |
|
An implication can be viewed as an obligation , a contract , or a commitment . The implication \(p \rightarrow q\) is false (the contract is broken; the obligation is unmet) only when \(p\) is true and \(q\) is false.
There are several important observations from this truth table about logical implication.
If \(q\) is true, then \(p \rightarrow q\) is always true.
If \(p\) is true and the implication correct (the obligation is upheld), then \(q\) can never be false.
“Falsity can imply anything.” If the hypothesis is false, then the implication is always true, regardless of the whether or not the conclusion is true.
Some of these observations may seem counter-intuitive at first. Let us clarify with some examples.
The truth value of implications
Let \(p\) be “that animal is a panda bear” and \(q\) be “that animal is black and white”. \(p \rightarrow q\) can be read as “if that animal is a panda bear, then that animal is black and white”.
If \(p\) is true, and that animal is indeed a panda bear (and the implication is correct), then it is also black and white. If \(q\) is true, and the animal is black and white, it might be a panda bear, but it might also be a cow.
From \(p \rightarrow q\) , we can say that knowing the animal is a panda bear is sufficient to know that the animal is black and white.
Valid implications can be formed from completely unrelated propositions. Moreover, if you begin with a nonsensical hypothesis, then one can construct valid (but equally nonsensical) implications. Falsity implies anything .
Absurd but valid implications
“If pigs can fly, then I am the pope.”
“If \(2+2=5\) , then lemons are purple.”
“If the sun is made of ice, then my father is Morgan Freeman”.
There are many equivalent ways to think about the implication \(p \rightarrow q\) .
If \(p\) , then \(q\)
\(p\) implies \(q\)
\(q\) when \(p\)
\(q\) , if \(p\)
\(q\) whenever \(p\)
\(q\) follows from \(p\)
\(p\) is sufficient for \(q\)
\(q\) is necessary for \(p\)
Necessity and Sufficiency
An implication connects propositions by a necessary or sufficient condition. From \(p \rightarrow q\) we get two relations:
That is, “if sufficient condition , then necessary condition ”.
Necessary and Sufficient
“If all birds have feathers, then a chicken is a type of bird.”
Knowing birds have feathers is sufficient information to conclude that a chicken is a type of bird. If a chicken is a type of bird, then chickens necessarily have feathers.
Fig. 1.1 Being in the inner circle is sufficient for being in the outer circle. Being in the outer circle is necessary for being in the inner circle. #
Biconditional #
For two propositions \(p\) and \(q\) , they can be connected by a biconditional as \(p \leftrightarrow q\) .
A biconditional is an double implication. A biconditional is true if both propositions have the same truth value. \(p \leftrightarrow q\) can be read as “ \(p\) if and only if \(q\) ”. A biconditional has the following truth table.
\(p\) | \(q\) | \(p \leftrightarrow q\) |
|---|---|---|
F | F |
|
F | T |
|
T | F |
|
T | T |
|
The biconditional \(p \leftrightarrow q\) can be expressed in many ways:
“ \(p\) if and only if \(q\) ”
“if \(p\) then \(q\) , and if \(q\) then \(p\) ”
“ \(p\) is necessary and sufficient for \(q\) ”
“ \(p\) iff \(q\) ”
Let \(p\) be “ \(2\) is an even number”. Let \(q\) be “ \(4\) is an even number”. \(p \leftrightarrow q\) is a biconditional and its truth value is true, since both \(p\) and \(q\) are true.
Tip (thinking in memes)
“The venn diagram is a circle” exactly means that the two subjects form a biconditional.
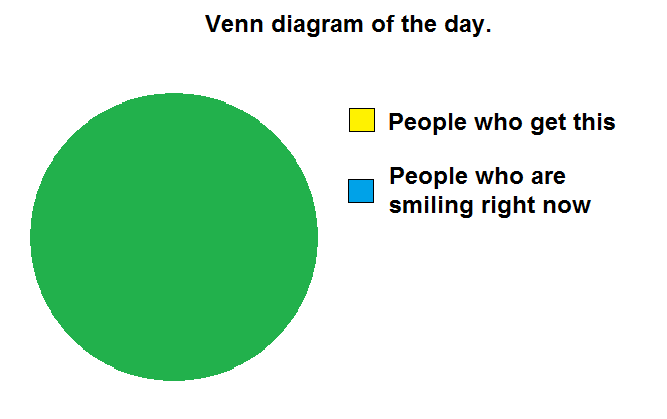
“The Earth is flat” \(\rightarrow\) “Pigeons are robots”
“Bats have wings” \(\rightarrow\) “Bats are birds”
“A square is a rectangle” \(\leftrightarrow\) “A square had four \(90^{\circ}\) interior angles”
“Spinach is green” \(\leftrightarrow\) “Penguins can fly”
True. “The Earth is flat” is false, and false implies anything!
False. An implication is false if the hypothesis is true meanwhile the conclusion is false. Bats have wings but are not birds. Therefore, the implication is false.
True. Both sides of the biconditional are true.
False. The left-hand side is true meanwhile the right-hand side is false.
Propositional Formulas #
In the previous section we saw 5 different logical connectives: \(\neg\) , \(\land\) , \(\lor\) , \(\rightarrow\) , and \(\leftrightarrow\) . Much like arithmetic formulas using addition, multiplication, division, etc., propositional formulas may use several connectives simultaneously.
Remember BEDMAS or PEDMAS ? Now we have “PaNCo DIB” (“ Panko Dib”)?
For logical connectives we have a similar order of precedence .
Parenthesis: always perform operations on expressions inside parentheses first.
Negation: apply negation to a proposition before binary connectives .
Conjunction: conjunction before disjunction
Disjunction: disjunction after conjunction, but before implication
Implication: \(\rightarrow\) after \(\land\) , \(\lor\)
Biconditional: \(\leftrightarrow\) after \(\land, \lor, \rightarrow\) .
Logical order of precendence
\(p \lor q \rightarrow \neg r\ \ \) is the same as \(\ \ (p \lor q) \rightarrow (\neg r)\)
\(p \lor \neg q \land r\ \ \) is the same as \(\ \ p \lor ( \ (\neg q)\ \land r)\)
Propositional variables need not be associated with a particular proposition or truth value. A propositional variable could be just that: a variable . Replacing the variables in a propositional formula with a truth value is called a truth assignment .
Definition (truth assignment)
A truth assignment is the assignment of a truth value ( true or false ) to a propositional variable. Equally, it is the replacement of a propositional variable with a truth value.
Much like logical connectives, propositional formulas will result in different truth values depending on the particular truth assignment on its consituent propositional variables. When at least one truth assignment exists so that a formula is true, that formula is said to be satisfiable .
Definition (satisfiable)
A propositional formula is satisfiable if its truth value can be true under some truth assignment. If every possible truth assignment makes the formula have false as its truth value, that formula is said to be unsatisfiable .
In order to determine the truth value of a propositional formula, and to determine if it is satisfiable, we can create a truth table .
Truth Tables #
Truth tables are tools for determining the truth values of propositional formulas.
The table is separated into two sets of columns:
The first set of columns represent each proposition (or propositional variable) in a formula.
The second set of columns represents the sub-formulas and formulas whose truth values are to be determined.
There must be one row in the table for every possible combination of truth values of the propositional variables. For example, in a formula with two variables, the possible combinations are: \((T,T), (T,F), (F,T), (F,F)\) .
3-variable truth table
Let \(p, q, r\) be propositional variables. A truth table for the formula \((p \land q) \lor r\) is:
\(p\) | \(q\) | \(r\) | \(p \land q\) | \((p \land q) \lor r\) |
|---|---|---|---|---|
F | F | F | F |
|
F | F | T | F |
|
F | T | F | F |
|
F | T | T | F |
|
T | F | F | F |
|
T | F | T | F |
|
T | T | F | T |
|
T | T | T | T |
|
Notice that every possible combination of truth values for \(p\) , \(q\) , and \(r\) is contained in this table. Since at least one choice of truth value for \(p\) , \(q\) , and \(r\) results in the formula being true, then this formula is satisfiable.
In a truth table, you begin by filling out the columns corresponding to each propositional variable. These columns represent every possible combination of truth values on those variables. Then, you add columns for each sub-formula, one at a time, building up to the final formula.
Consider the formula \(p \land q \land r \ \lor\ \neg q \land r \rightarrow p\) . By order of precendence, this is equal to \((\ (p \land q \land r) \ \lor\ ((\neg q) \land r)\ ) \rightarrow p\) This contains several sub-formulas which we can parse:
\(\neg q \land r\)
\(p \land q\)
\((p \land q) \land r\)
\((p \land q \land r) \lor (\neg q \land r)\)
\((\ (p \land q \land r) \lor (\neg q \land r)\ ) \rightarrow p\)
To be as explicit as possible, we could create a truth table with 3 + 6 = 9 columns (3 variables, 6 sub-formulas). But this is excessive. For example, we could directly compute \((\neg q \land r)\) and \((p \land q \land r)\) . This gives the following truth table.
A large truth table
A truth table for the propositional formula \(p \land q \land r \ \lor\ \neg q \land r \rightarrow p\) .
\(p\) | \(q\) | \(r\) | \(p \land q \land r\) | \(\neg q \land r\) | \((p \land q \land r) \lor (\neg q \land r)\) | \((p \land q \land r) \lor (\neg q \land r) \rightarrow p\) |
|---|---|---|---|---|---|---|
F | F | F | F | F | F |
|
F | F | T | F | T | T |
|
F | T | F | F | F | F |
|
F | T | T | F | F | F |
|
T | F | F | F | F | F |
|
T | F | T | F | T | T |
|
T | T | F | F | F | F |
|
T | T | T | T | F | T |
|
Construct a truth table
Give a truth table for the propositional formula \(p \land r \rightarrow q \lor \neg r\)
\(p \land r \rightarrow q \lor \neg r\ \ \ \) is equal to \(\ \ \ (p \land r) \rightarrow (q \lor (\neg r)\ )\)
\(p\) | \(q\) | \(r\) | \(p \land r\) | \(q \lor \neg r\) | \(p \land r \rightarrow q \lor \neg r\) |
|---|---|---|---|---|---|
F | F | F | F | T |
|
F | F | T | F | F |
|
F | T | F | F | T |
|
F | T | T | F | T |
|
T | F | F | F | T |
|
T | F | T | T | F |
|
T | T | F | F | T |
|
T | T | T | T | T |
|
Implication, Inverse, Converse, and Contrapositive #
Now that we have seen propositional formulas and truth tables, let’s revisit implications. This connective has many related conditionals.
Consider the propositional formula \(p \rightarrow q\) . Then, we have:
Converse : \(q \rightarrow p\)
Inverse : \(\neg p \rightarrow \neg q\)
Contrapositive : \(\neg q \rightarrow \neg p\)
A conditional and its inverse
The proposition “if it is raining, then I wear a jacket” is a conditional statement. Its inverse is “if it is not raining I do not wear a jacket”.
Notice from this previous example than an implication and its inverse are not exactly the same. If the conditional “if it is raining, then I wear a jacket” is true , that is not the same as its inverse. Indeed, you might still wear a jacket even if its not raining. Maybe you’re just cold.
An implication is not equivalent to its converse or inverse. However, it is equivalent to its contrapositive. See Logical Equivalences and Exercises .
1.1.2. Applications #
There are many many applications of propositional logic. You will explore many more of them in other courses on logic, computer architecture, theoretical computer science, and more.
In this section we review a small sampling of applications:
Translating English to logic.
Boolean searches.
Formal specifications of software and computer systems.
Solving logic puzzles.
Translating English to Propositional Logic #
To convert an English sentence to a propositional formula, there are two significant steps. First, find the atomic propositions , the smallest clauses of the sentence which do not contain connectives. Represent each such proposition as a unique variable. Second, determine the appropriate logical connectives for those propositions.
A first logical translation
“If it is raining and I am going outside, I bring an umbrella.”
Let \(p\) be “it is raining”
Let \(q\) be “I am going outside”
Let \(r\) be “I bring an umbrella”
Choosing the corrective connectives gives the logical translation of this sentence:
A second logical translation
“The dog is large and friendly or small and boisterous”
Let \(p\) be “the dog is large”
Let \(q\) be “the dog is friendly”
Let \(r\) be “the dog is small”
Let \(t\) be “the dog is boisterous”
Note the ambiguity of the previous example. Did the English sentence assume an exlusive or ? Probably. Then, a correct translation might be \((p \land q) \oplus (r \land t)\) .
Boolean Searches #
Boolean , from mathematician George Boole, refers to a special kind of mathematics that deals with turth values: true and false . Boolean algebra is a set of rules for manipulating formulas containing variables and truth values. This is very similar to, but slightly distinct from propositional logic. We will not explore Boolean algebra in this course.
Boolean searches are about using logical connectives to help search through datasets and filter pieces of data. This includes databases and internet search engines.
Consider a search using two keywords “foo” and “bar”.
AND is used to find records which contain both “foo” and “bar”.
OR is used to find records which contain “foo” or “bar” or both.
NOT is used to exclude records which do contain a keyword.
Web Searches
Consider the key words “London”, “Beer”, “England”, and “Cider”
If we are looking for places to find beer in London, England we might search:
London AND England AND Beer
In most search engines, the AND is implicit, and we can simply search “London England Beer”.
If we are looking for places to find beer or cider in London, England we might search:
London England Beer | Cider
The AND s are implicit: “London AND England AND (Beer OR Cider)”
If we are looking for places to find beer in London, Ontario we might try to exclude entries for London, England. Searching for:
(London AND Beer) NOT England
Search engines often use the minus sign to denote NOT : “London Beer -England”
Formal Specifications #
In software, computer, and electrical engineering, the requirements of a system, software, or defice must often meet very precise specifications.
These specifications are sometimes easy to express. For example, “the circuit carries 115-125 volts”. For softare in particular, its requirements are often expressed as (ambiguous) natural language requirements. Those requirements must be translated into precise logical statements.
Logical Specification
“Mute all notifications during buisness hours when the user’s status is not available.”
Let \(p\) be “it is during business hours”.
Let \(q\) be “the user’s status is set to available”.
Let \(r\) be “mute all notifications”.
A propositional formula for this specification is:
Propositional logic can also be used to determine if the collection of all requirements for a system is consistent .
Definition (consistent)
A set of propositional formulas is consistent if there exsists at least one truth assignment so that every proposition is simultaneously true.
Notice that consistency is not the same as every formula in a set being satisfiable. The formulas must be simultaneously satisfied by the same truth assignment.
One way to determine consistency is as follows. Given a collection of propositions \(p_1,p_2,\ldots,p_n\) , the propositions are consistent if their conjunction is satisfiable. That is, the following formula has at least one truth assignment that makes it true:
To determine the consistency of a requirement set, we must first build propositional formulas for each requirement. Where the same “clause” exists in multiple requirements (recall Translating English to Propositional Logic ), we should re-use that propositional variable. Second, we must assign true or false to each variable so that every formula is simultaneously true. If no such assignment exists, the set of requirements is said to be inconsistent .
Let us consider an electronic messaging network which requires that all sent messages are certain to be received. This behaviour might be modelled as the following specifications:
Messages remain in the outbound message queue until they have been received by the recipient.
An unreceived message is either a draft or is in the outbound message queue.
Received messsages cannot be drafts.
Is this set of requirements consistent?
Let \(p\) be “message is in the outbound message queue”.
Let \(q\) be “message is received”.
Let \(r\) be “message is a draft”.
\(p \rightarrow \neg q\)
\(\neg q \rightarrow (p \lor r)\)
\(q \rightarrow \neg r\)
\(p\) | \(q\) | \(r\) | \(p \rightarrow \neg q\) | \(\neg q \rightarrow (p \lor r)\) | \(q \land \neg r\) |
|---|---|---|---|---|---|
F | F | F |
|
|
|
F | F | T |
|
|
|
F | T | F |
|
|
|
F | T | T |
|
|
|
T | F | F |
|
|
|
T | F | T |
|
|
|
T | T | F |
|
|
|
T | T | T |
|
|
|
Since at least one truth assignment simultaneously satisfies all equations, namely \(p := F, q := T, r := F\) , this set of requirements is consistent . In the language of this problem, that means the message is received and is not a draft and is not in the outbound queue.
Solving logic puzzles #
Many puzzles are based around logical arguments and reasoning. So solve such puzzles, propositional logic is a very useful tool. The idea is to model the elements of the puzzle as propositional formula(s), and use those formulas to determine if the formula(s) are satisfiable, consistent, etc., depending on the puzzle.
Let’s see an example.
Activity (Knights and Knaves)
Suppose you are on an island with two kinds of people:
knights , who always tell the truth; and
knaves , who always lie.
You meet two people, \(A\) and \(B\) . \(A\) says “ \(B\) is a knight.” \(B\) says “the two of us are different kinds of people”.
What kind of people are \(A\) and \(B\) ?
\(A\) and \(B\) are both knaves.
Let \(p\) be “ \(A\) is a knight”. Let \(q\) be “ \(B\) is a knight”. The statement “the two of us are different kinds of people” can be represented as \((p \land \neg q) \lor (\neg p \land q)\) .
Assume \(A\) is a knight and therefore \(p\) is true. Then, their statement “ \(B\) is a knight” must be true and therefore \(q\) is true. If \(B\) is a knight, then the formula \((p \land \neg q) \lor (\neg p \land q)\) should be true. However, this formula is false if both \(p\) and \(q\) are true.
Assume \(A\) is a knave (i.e. \(\neg p\) is true). Then, their statement “ \(B\) is a knight” must be false (i.e. \(\neg q\) is true). Therefore, \(B\) is a knave and their statement should be a lie. Both \(p\) and \(q\) being false makes \((p \land \neg q) \lor (\neg p \land q)\) false, which is consistent.

1.1.3. Logical Equivalences #
Propositional logic is the foundation of more complex logical systems and of formal mathematical proofs. One particular kind of proof, an “equivalence proof”, proves that one thing is equivalent to another through a sequence of equivalences.
What is an equivalence? Well, the first quesiton to ask is: what is a tautology?
Definition (tautology)
A propositional formula that is always true, for every possible truth assignment, is a tautology .
A proposition that is not a tautology is either a contradiction or a contingency .
Definition (contradiction)
A propositional formula that is always false, for every possible truth assignment, is a contradiction .
Definition (contingency)
A propositional formula that is neither a tautology nor a contradiction is a contingency .
Logically Equivalent #
Two propositional formulas, say \(p\) and \(q\) , are logically equivalent if \(p \leftrightarrow q\) is a tautology. When this is the case, we may write \(p \iff q\) or \(p \equiv q\) .
A simple and explicit way to determine if two expressions are logically equivalent is if their two columns in a truth table are identical.
Logically equivalent truth table
\(p\) | \(q\) | \(\neg p\) | \(p \rightarrow q\) | \(\neg p \lor q\) |
|---|---|---|---|---|
F | F | T |
|
|
F | T | T |
|
|
T | F | F |
|
|
T | T | F |
|
|
There are several logical equivalences which would be good to memorize . They are similar to many laws of arithmetic. For example, we know \(x \times 0 = 0\) regardless of the value of \(x\) .
Identity Laws
Annihilation Laws
Idempotent Laws
Complementation Laws
Double negation
\(p \land T \equiv p\)
\(p \land F \equiv F\)
\(p \land p \equiv p\)
\(p \land \neg p \equiv F\)
\(\neg (\neg p) \equiv p\)
\(p \lor F \equiv p\)
\(p \lor T \equiv T\)
\(p \lor p \equiv p\)
\(p \lor \neg p \equiv T\)
There are also interesting properties of logical connectives between two or more propositional variables.
Commutativity
Associativity
Distributivity
De Morgan’s Laws
\(p \land q \equiv q \land p\)
\(p \land (q \land r) \equiv (p \land q) \land r\)
\(p \land (q \lor r) \equiv (p \land q) \lor (p \land r)\)
\(p \land (p \lor q) \equiv p\)
\(\neg (p \land q) \equiv \neg p \lor \neg q\)
\(p \lor q \equiv q \lor p\)
\(p \lor (q \lor r) \equiv (p \lor q) \lor r\)
\(p \lor (q \land r) \equiv (p \lor q) \land (p \lor r)\)
\(p \lor (p \land q) \equiv p\)
\(\neg (p \lor q) \equiv \neg p \land \neg q\)
De Morgan’s Laws are very important. These laws explain how negation distributes over a conjunction and disjunction. In particular, it turns disjunctions into conjunctions, and vice versa.
In these laws and properties, we can replace any propositional variable with an entire propositional formula, and the law is still correct.
Variable-expression replacement
Let \(p := (\neg a \land b) \lor c\) .
These laws and properties can be used as building blocks to prove that certain expressions are logically equivalent. Before we see that process, let’s see some more interesting logical equivalences.
More logical equivalences
\((p \rightarrow q) \equiv \neg p \lor q\)
\((p \rightarrow q) \land (p \rightarrow r) \equiv p \rightarrow (q \land r)\)
\((p \rightarrow r) \land (q \rightarrow r) \equiv (p \lor q) \rightarrow r\)
\(p \leftrightarrow q \equiv (p \rightarrow q) \land (q \rightarrow p)\)
\(p \leftrightarrow q \equiv \neg p \leftrightarrow \neg q\)
\(p \leftrightarrow q \equiv (p \land q) \lor (\neg p \land \neg q)\)
Draw the truth table for some of the above examples to prove to yourself that the two expressions are logically equivalent.
Equivalence proof #
We can show two expressions, say \(A\) and \(B\) , are logically equivalent by constructing a sequence of logically equivalent statements \(E_i\) , beginning with \(A\) and ending with \(B\) .
A first equivalence proof
Prove that \(p \land (\neg p \lor q) \equiv p\land q\) .
Whenever we use propositional logic, we will return to equivalence proofs and truth tables. It is important that you really understand the manipulation and equivalency of propositional truth tables.
Prove that \(p \lor (p \land q) \lor (\neg p \land r) \equiv (p\land q) \lor p \lor r\) .
1.1.4. Exercises #
Basic propositions #.
Exercise 1.1
If a propositional formula has 5 variables, how many rows are needed in its truth table?
Solution to Exercise 1.1
\(\mathbf{32}\) . Each variable has two choices: true of false. 5 variables means there are \(2 \times 2 \times 2 \times 2 \times 2 = 2^5 = 32\) possible combinations of truth values.
Exercise 1.2
Express the following English sentence as a propositional formula. “If it is snowing I wear a jacket and I wear mittens.”
Solution to Exercise 1.2
\(p\) : It is snowing
\(q\) : I wear a jacket
\(r\) : I wear mitterns
Exercise 1.3
Express the following English sentence as a propositional formula. “When I am at the beach or I go swimming, I wear a swimsuit.”
Solution to Exercise 1.3
\(p\) : I am at the beach
\(q\) : I go swimming
\(r\) : I wear a swimsuit
Exercise 1.4
Classify each of the following statements as true or false.
“ \(4 = 2+2\) and \(7 < \sqrt{50}\) ”
“ \(4 = 2+2 \rightarrow 7 < \sqrt{50}\) ”
“ \(4 \neq 2 +2 \rightarrow 7 < \sqrt{50}\) ”
“ \(4 = 2 +2 \rightarrow 7 \geq \sqrt{50}\) ”
Solution to Exercise 1.4
True . Both clauses are true.
True . Both premise and conclusion are true.
True . The hypothesis is false, therefore true.
False . The premise is true, but the conclusion is false.
Exercise 1.5
Give the negation of each of the following compound statements.
“Either \(a^2 > 0\) or \(a\) is not a real number.”
“ \(x = \pm 1\) ”
“ \(x\) is a real number and \(x^2 + 1 = 0\) ”
Solution to Exercise 1.5
“ \(a^2 \leq 0\) and \(a\) is a real number”; also “ \(a = 0\) ”
“ \(x \neq 1\) and \(x \neq -1\) ”
“ \(x\) is not a real number or \(x^2 + 1 \neq 0\) ”
Exercise 1.6
Give the converse, inverse, and contrapositive of each of the following implications.
“If \(\frac{a}{b}\) and \(\frac{b}{c}\) are integers, then \(\frac{a}{c}\) is an integer.”
“Every Eulerian graph is connected”.
“ \(ab = 0 \rightarrow a = 0\) or \(b = 0\) ”.
Solution to Exercise 1.6
Converse: “If \(\frac{a}{c}\) is an integer then \(\frac{a}{b}\) and \(\frac{b}{c}\) are integers”
Inverse: “If \(\frac{a}{b}\) is not an integer or \(\frac{b}{c}\) is not an integer then \(\frac{a}{c}\) is not an integer.”
Contrapositive: “If \(\frac{a}{c}\) is not an integer then \(\frac{a}{b}\) is not an integer or \(\frac{b}{c}\) is not an integer”
Converse: “Every connected graph is Eulerian”
Inverse: “Every non-Eulerian graph is not connected.”
Contrapositive: “Every non-connected graph is not Eulerian.”
Converse: “ \(a=0\) or \(b=0\) \(\rightarrow\) \(ab=0\) ”
Inverse: “ \(ab \neq 0 \rightarrow a \neq 0\) and \(b \neq 0\) ”
Contrapositive: “ \(a \neq 0\) and \(b \neq 0 \rightarrow ab \neq 0\)
Exercise 1.7
For each of the following propositional formulas, determine which are satisfiable. If they are satisfiable, give a truth assignment which satisfies the formula.
\(p \land (\neg q \lor \neg r) \land (q \lor \neg p)\)
\(p \land (q \lor \neg p) \land (\neg q \lor \neg p) \land r\)
\((p \land q \land \neg r) \lor (p \land \neg q \land \neg r)\)
Solution to Exercise 1.7
\((p, q, r) := (T, T, F)\)
Not satisfiable
\((p,q,r) := (T, T, F)\) or \((T, F, F)\)
Applications #
Exercise 1.8
Julie and Jamie are identical twins. One of then always lies and one of them always tells the truth. Suppose you meet one of them. What 3-word question (with a yes/no answer) can you ask to determine which twin is in front of you? You do not know which twin lies.
Solution to Exercise 1.8
“Does Julie lie?”
Suppose you meet Julie and Julie tells the turth. Julie will reply “no”.
Suppose you meet Julie and Julie lies. Julie will reply “no” (i.e. “no, Jamie lies”).
Suppose you meet Jamie and Jamie tells the truth. Jamie will reply “yes”.
Suppose you meet Jamie and Jamie lies. Jamie will reply “yes” (i.e. “yes, Julie lies”).
Exercise 1.9
Define the basic clauses of each of the following statements as propositional variables. Then, express each of the following compound statements as propositional formulas. Finally, is this set of propositions consistent? If so, give a truth assignment which shows they are consistent.
The campus server does not work if the internet is off.
Students can skype during the test when the prof is distracted.
If the classroom phone does not ring then the prof is not distracted.
Students cannot skype during the test unless the internet is on.
If the classroom phone rings then the campus server works.
Solution to Exercise 1.9
\(I :=\) “internet is on”
\(C :=\) “the campus server works”
\(D :=\) “the professor is distracted”
\(S :=\) “students can Zoom during the test”
\(R :=\) “the classroom phone rings”
\(\neg I \rightarrow \neg C\)
\(D \rightarrow S\)
\(\neg R \rightarrow \neg D\)
\(S \rightarrow I\) ; \(\neg I \rightarrow \neg S\) ; “A unless B” translates logically to “A if not B”
\(R \rightarrow C\)
To check consistency, we need to see if the following conjunction is satisfiable.
This is satisfiable with: \((I, S, R, D, C) := (T, T, T, T, T)\)
Logical Equivalences #
Exercise 1.10
Show that \(p \rightarrow q\) is logically equivalent to \(\neg q \rightarrow \neg p\) .
Exercise 1.11
Prove De Morgan’s law \(\neg (p \land q) \equiv \neg p \lor \neg q\) by a truth table.
Solution to Exercise 1.11
\(p\) | \(q\) | \(\neg (p \land q)\) | \(\neg p \lor \neg q\) |
|---|---|---|---|
F | F |
|
|
F | T |
|
|
T | F |
|
|
T | T |
|
|
Exercise 1.12
If \((p \land q) \lor ((\neg p) \land q \land r)\) is logically equivalent to \((p \land q \land r) \lor (p \land q)\) , show their biconditional is a tautology. If not, give a truth assignment which results in different truth values for each formula.
Exercise 1.13
Show that the following expressions are logically equivalent. Do this by (a) truth tables, and (b) logical equivalences.
Exercise 1.14
Prove that \(p \lor (p \land q) \lor (\neg p \land r) \equiv p \lor r\) .
Solution to Exercise 1.14
Exercise 1.15
Prove that \(\neg (p \lor (\neg p \land q)) \equiv \neg p \land \neg q\) .
Solution to Exercise 1.15
Let \(A\) be \(\neg p \land q\) .
Exercise 1.16
Prove that \(p \land r \land (\neg q \lor p) \equiv p\land r\) .

Section 1.2: Truth Assignments
- Section 1.2: Problem 1 Solution
- Section 1.2: Problem 2 Solution
- Section 1.2: Problem 3 Solution
- Section 1.2: Problem 4 Solution
- Section 1.2: Problem 5 Solution
- Section 1.2: Problem 6 Solution
- Section 1.2: Problem 7 Solution
- Section 1.2: Problem 8 Solution
- Section 1.2: Problem 9 Solution
- Section 1.2: Problem 10 Solution
- Section 1.2: Problem 11 Solution
- Section 1.2: Problem 12 Solution
- Section 1.2: Problem 13 Solution
- Section 1.2: Problem 14 Solution
- Section 1.2: Problem 15 Solution
- Section 1.2: Problem 16-A Solution
Section 1.2: Problem 1 Solution »
- Every finite set of wffs has an equivalent independent subset, but this is not true, in general, for an infinite set of wffs.
- The substitution principle : if a wff is a tautology, then by substituting wffs for sentence symbols we still get a tautology.
1.3 Truth tables
We’ve seen what a WFF is. It’s important to remember that a WFF like ( p ∧ q ) isn’t true or false on its own: that will depend on the truth or falsity of the statements represented by the propositional variables p and q . The aim of the next couple of sections is to see how, once we decide whether the propositional variables in a WFF are true or false, we can give a truth value to the whole WFF.
The way we do this is by making a truth-table definition for each connective of how the truth value of a WFF using that connective depends on the truth values of the WFFs it connects. We do this in such a way that the connective behaves like the informal logical idea it is supposed to represent: for example, ∧ is supposed to represent and so we will define ( ϕ ∧ ψ ) to be true if and only if ϕ and ψ are both true. Once we’ve done this for every connective, we can determine the truth value of any WFF by looking at the simplest formulas contained in it, determining their truth values using our tables, and working our way upwards until we have the truth value of the whole formula.
1.3.1 Truth assignments for propositional variables
Let’s start with giving truth values to propositional variables. Here and elsewhere T means true and F means false.
Definition 1.3.1 .
A truth assignment for a set V of propositional variables is a function v : V → { T , F } .
(A better name for this concept would be ‘truth-value assignment’ since a truth assignment can make variables false as well as true, but this is the conventional name.)
Example 1.3.1 .
If p and q are propositional variables and V = { p , q } then there is a truth assignment v for V such that v ( p ) = T and v ( q ) = F .
This is one of the four different truth assignments for a set of two propositional variables. In general, if you have n propositional variables then there are 2 n different truth assignments for those variables, since each variable must be given one of two different truth values.
1.3.2 Extending a truth assignment to WFFs
Given a truth assignment for some propositional variables, we would like to extend it to get a truth value for all the WFFs using those variables in a way that takes into account the intended meaning of the logical connectives. This is a difficult problem for complex WFFs. For example, if you have a truth assignment which makes p and r true and q false, what should the truth value of the following WFF be?
In order to approach the problem of extending a truth assignment so that it gives a sensible truth value to any WFF, suppose that we somehow already knew what truth values we were going to assign to the WFFs ϕ and ψ . What truth value should we give to the WFF ( ϕ ∧ ψ ) ? We are free to choose this of course, but since ∧ is supposed to represent the ordinary usage of the word “and” it would be sensible to assign ( ϕ ∧ ψ ) the value true if both ϕ and ψ were assigned true, and false otherwise.
This idea is summed up in the following truth table for ∧ :
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
The meaning of the table is that given a truth assignment v : V → { T , F } , our method of assigning a truth value to a WFF ( ϕ ∧ ψ ) using the variables V will be as follows. Row 1 means that if v ( ϕ ) = T and v ( ψ ) = T then v ( ( ϕ ∧ ψ ) ) will be T . Row 2 means that if v ( ϕ ) = T and v ( ψ ) = F then v ( ( ϕ ∧ ψ ) ) will be F , and so on.
Another way to think about this truth table is to use it to define ∧ as a way to combine two truth values into another truth value, just like + combines two numbers into another number. We let T ∧ T = T , T ∧ F = F , F ∧ T = F , and T ∧ F = F . The advantage of this is that it lets us rewrite the last paragraph in a single sentence: we will define v ( ( ϕ ∧ ψ ) ) to be v ( ϕ ) ∧ v ( ψ ) .
Here are the truth tables for the other connectives in our language.
| T | F |
| F | T |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Similarly to what we did for ∧ , we regard all of our connectives not just as symbols to be used in WFFs but as ways of combining truth values. For example, we define ¬ T = F , T ∨ F = T , and F ⟹ T = T .
People often find the truth table for implies confusing, especially the final two rows where ϕ is false. These last two rows tell us that ( ϕ ⟹ ψ ) is true whenever ϕ is false, regardless of the truth value given to ψ . If you’d like to read more about why this truth table is a sensible way to define truth values for statements containing implies, this short piece of writing by (Fields medallist) Tim Gowers , or this longer version is good.

- Table of Contents
- Random Entry
- Chronological
- Editorial Information
- About the SEP
- Editorial Board
- How to Cite the SEP
- Special Characters
- Advanced Tools
- Support the SEP
- PDFs for SEP Friends
- Make a Donation
- SEPIA for Libraries
- Entry Contents
Bibliography
Academic tools.
- Friends PDF Preview
- Author and Citation Info
- Back to Top
Truth Values
Truth values have been put to quite different uses in philosophy and logic, being characterized, for example, as:
- primitive abstract objects denoted by sentences in natural and formal languages,
- abstract entities hypostatized as the equivalence classes of sentences,
- what is aimed at in judgements,
- values indicating the degree of truth of sentences,
- entities that can be used to explain the vagueness of concepts,
- values that are preserved in valid inferences,
- values that convey information concerning a given proposition.
Depending on their particular use, truth values have been treated as unanalyzed, as defined, as unstructured, or as structured entities.
The notion of a truth value has been explicitly introduced into logic and philosophy by Gottlob Frege—for the first time in Frege 1891, and most notably in his seminal paper (Frege 1892). Although it was Frege who made the notion of a truth value to one of the central concepts of semantics, the idea of special semantical values, however, was anticipated by Boole and Peirce already, see the survey article on a “history of truth values” by Béziau (2012). According to Kneale and Kneale (1962: 413), Boole’s system contains all that is needed for its interpretation “in terms of truth values of propositions”, and as Church (1956: 17) remarks, the “explicit use of two truth-values appears for the first time in a paper by C.S. Peirce in the American Journal of Mathematics , vol. 7 (1885), pp. 180–202”. Frege conceived this notion as a natural component of his language analysis where sentences, being saturated expressions, are interpreted as a special kind of names, which refer to (denote, designate, signify) a special kind of objects: truth values. Moreover, there are, according to Frege, only two such objects: the True ( das Wahre ) and the False ( das Falsche ):
Every assertoric sentence … is to be regarded as a proper name, and its Bedeutung , if it has one, is either the True or the False. (Frege 1892, trans. Beaney 1997: 158)
This new and revolutionary idea has had a far reaching and manifold impact on the development of modern logic. It provides the means to uniformly complete the formal apparatus of a functional analysis of language by generalizing the concept of a function and introducing a special kind of functions, namely propositional functions, or truth value functions, whose range of values consists of the set of truth values. Among the most typical representatives of propositional functions one finds predicate expressions and logical connectives. As a result, one obtains a powerful tool for a conclusive implementation of the extensionality principle (also called the principle of compositionality), according to which the meaning of a complex expression is uniquely determined by the meanings of its components. On this basis one can also discriminate between extensional and intensional contexts and advance further to the conception of intensional logics. Moreover, the idea of truth values has induced a radical rethinking of some central issues in the philosophy of logic, including: the categorial status of truth, the theory of abstract objects, the subject-matter of logic and its ontological foundations, the concept of a logical system, the nature of logical notions, etc.
In the following, several important philosophical problems directly connected to the notion of a truth value are considered and various uses of this notion are explained.
1.1 Functional analysis of language and truth values
- Supplementary Document: The Slingshot Argument
1.3 The ontology of truth values
2.1 logic as the science of logical values, 2.2 many-valued logics, truth degrees and valuation systems, 2.3 truth values, truth degrees, and vague concepts.
- Supplementary Document: Suszko’s Thesis
3.1 The notion of a logical order
- Supplementary Document: Generalized truth values and multilattices
4. Concluding remarks
Other internet resources, related entries, 1. truth values as objects and referents of sentences.
The approach to language analysis developed by Frege rests essentially on the idea of a strict discrimination between two main kinds of expressions: proper names (singular terms) and functional expressions. Proper names designate (signify, denote, or refer to) singular objects, and functional expressions designate (signify, denote, or refer to) functions. [Note: In the literature, the expressions ‘designation’, ‘signification’, ‘denotation’, and ‘reference’ are usually taken to be synonymous. This practice is used throughout the present entry.] The name ‘Ukraine’, for example, refers to a certain country, and the expression ‘the capital of’ denotes a one-place function from countries to cities, in particular, a function that maps Ukraine to Kyiv (Kiev). Whereas names are “saturated” (complete) expressions, functional expressions are “unsaturated” (incomplete) and may be saturated by applying them to names, producing in this way new names. Similarly, the objects to which singular terms refer are saturated and the functions denoted by functional expression are unsaturated. Names to which a functional expression can be applied are called the arguments of this functional expression, and entities to which a function can be applied are called the arguments of this function. The object which serves as the reference for the name generated by an application of a functional expression to its arguments is called the value of the function for these arguments. Particularly, the above mentioned functional expression ‘the capital of’ remains incomplete until applied to some name. An application of the function denoted by ‘the capital of’ to Ukraine (as an argument) returns Kyiv as the object denoted by the compound expression ‘the capital of Ukraine’ which, according to Frege, is a proper name of Kyiv. Note that Frege distinguishes between an \(n\)-place function \(f\) as an unsaturated entity that can be completed by and applied to arguments \(a_1\),…, \(a_n\) and its course of values , which can be seen as the set-theoretic representation of this function: the set
Pursuing this kind of analysis, one is very quickly confronted with two intricate problems. First , how should one treat declarative sentences ? Should one perhaps separate them into a specific linguistic category distinct from the ones of names and function symbols? And second , how—from a functional point of view—should one deal with predicate expressions such as ‘is a city’, ‘is tall’, ‘runs’, ‘is bigger than’, ‘loves’, etc., which are used to denote classes of objects, properties of objects, or relations between them and which can be combined with (applied to) singular terms to obtain sentences? If one considers predicates to be a kind of functional expressions, what sort of names are generated by applying predicates to their arguments, and what can serve as referents of these names, respectively values of these functions?
A uniform solution of both problems is obtained by introducing the notion of a truth value . Namely, by applying the criterion of “saturatedness” Frege provides a negative answer to the first of the above problems. Since sentences are a kind of complete entities, they should be treated as a sort of proper names, but names destined to denote some specific objects, namely the truth values: the True and the False . In this way one also obtains a solution of the second problem. Predicates are to be interpreted as some kind of functional expressions, which being applied to these or those names generate sentences referring to one of the two truth values. For example, if the predicate ‘is a city’ is applied to the name ‘Kyiv’, one gets the sentence ‘Kyiv is a city’, which designates the True (i.e., ‘Kyiv is a city’ is true ). On the other hand, by using the name ‘Mount Everest’, one obtains the sentence ‘Mount Everest is a city’ which clearly designates the False , since ‘Mount Everest is a city’ is false .
Functions whose values are truth values are called propositional functions . Frege also referred to them as concepts ( Begriffe ). A typical kind of such functions (besides the ones denoted by predicates) are the functions denoted by propositional connectives. Negation, for example, can be interpreted as a unary function converting the True into the False and vice versa , and conjunction is a binary function that returns the True as a value when both its argument positions are filled in by the True , etc. Propositional functions mapping \(n\)-tuples of truth values into truth values are also called truth-value functions .
Frege thus in a first step extended the familiar notion of a numerical function to functions on singular objects in general and, moreover, introduced a new kind of singular objects that can serve as arguments and values of functions on singular objects, the truth values. In a further step, he considered propositional functions taking functions as their arguments. The quantifier phrase ‘every city’, for example, can be applied to the predicate ‘is a capital’ to produce a sentence. The argument of the second-order function denoted by ‘every city’ is the first-order propositional function on singular objects denoted by ‘is a capital’. The functional value denoted by the sentence ‘Every city is a capital’ is a truth value, the False .
Truth values thus prove to be an extremely effective instrument for a logical and semantical analysis of language. [ 1 ] Moreover, Frege provides truth values (as proper referents of sentences) not merely with a pragmatical motivation but also with a strong theoretical justification. The idea of such justification, that can be found in Frege 1892, employs the principle of substitutivity of co-referential terms, according to which the reference of a complex singular term must remain unchanged when any of its sub-terms is replaced by an expression having the same reference. This is actually just an instance of the compositionality principle mentioned above. If sentences are treated as a kind of singular terms which must have designations, then assuming the principle of substitutivity one “almost inevitably” (as Kurt Gödel (1944: 129) explains) is forced to recognize truth values as the most suitable entities for such designations. Accordingly, Frege asks:
What else but the truth value could be found, that belongs quite generally to every sentence if the reference of its components is relevant, and remains unchanged by substitutions of the kind in question? (Geach and Black 1952: 64)
The idea underlying this question has been neatly reconstructed by Alonzo Church in his Introduction to Mathematical Logic (1956: 24–25) by considering the following sequence of four sentences:
C1–C4 present a number of conversion steps each producing co-referential sentences. It is claimed that C1 and C2 must have the same designation by substitutivity, for the terms ‘the author of Waverley ’ and ‘the man who wrote 29 Waverley Novels altogether’ designate one and the same object, namely Walter Scott. And so must C3 and C4, because the number, such that Sir Walter Scott is the man who wrote that many Waverley Novels altogether is the same as the number of counties in Utah, namely 29. Next, Church argues, it is plausible to suppose that C2, even if not completely synonymous with C3, is at least so close to C3 “so as to ensure its having the same denotation”. If this is indeed the case, then C1 and C4 must have the same denotation (designation) as well. But it seems that the only (semantically relevant) thing these sentences have in common is that both are true. Thus, taken that there must be something what the sentences designate, one concludes that it is just their truth value. As Church remarks, a parallel example involving false sentences can be constructed in the same way (by considering, e.g., ‘Sir Walter Scott is not the author of Waverley ’).
This line of reasoning is now widely known as the “slingshot argument”, a term coined by Jon Barwise and John Perry (in Barwise and Perry 1981: 395), who stressed thus an extraordinary simplicity of the argument and the minimality of presuppositions involved. Stated generally, the pattern of the argument goes as follows (cf. Perry 1996). One starts with a certain sentence, and then moves, step by step, to a completely different sentence. Every two sentences in any step designate presumably one and the same thing. Hence, the starting and the concluding sentences of the argument must have the same designation as well. But the only semantically significant thing they have in common seems to be their truth value. Thus, what any sentence designates is just its truth value.
A formal version of this argument, employing the term-forming, variable-binding class abstraction (or property abstraction) operator λ\(x\) (“the class of all \(x\) such that” or “the property of being such an \(x\) that”), was first formulated by Church (1943) in his review of Carnap’s Introduction to Semantics . Quine (1953), too, presents a variant of the slingshot using class abstraction, see also (Shramko and Wansing 2009a). Other remarkable variations of the argument are those by Kurt Gödel (1944) and Donald Davidson (1967, 1969), which make use of the formal apparatus of a theory of definite descriptions dealing with the description-forming, variable-binding iota-operator (ι\(x\), “the \(x\) such that”). It is worth noticing that the formal versions of the slingshot show how to move—using steps that ultimately preserve reference—from any true (false) sentence to any other such sentence. In view of this result, it is hard to avoid the conclusion that what the sentences refer to are just truth values.
The slingshot argument has been analyzed in detail by many authors (see especially the comprehensive study by Stephen Neale (Neale 2001) and references therein) and has caused much controversy notably on the part of fact-theorists, i.e., adherents of facts, situations, propositions, states of affairs, and other fact-like entities conceived as alternative candidates for denotations of declarative sentences. Also see the supplement on the slingshot argument .
1.2 Truth as a property versus truth as an object
Truth values evidently have something to do with a general concept of truth. Therefore it may seem rather tempting to try to incorporate considerations on truth values into the broader context of traditional truth-theories, such as correspondence, coherence, anti-realistic, or pragmatist conceptions of truth. Yet, it is unlikely that such attempts can give rise to any considerable success. Indeed, the immense fruitfulness of Frege’s introduction of truth values into logic to a large extent is just due to its philosophical neutrality with respect to theories of truth. It does not commit one to any specific metaphysical doctrine of truth. In one significant respect, however, the idea of truth values contravenes traditional approaches to truth by bringing to the forefront the problem of its categorial classification.
In most of the established conceptions, truth is usually treated as a property. It is customary to talk about a “truth predicate” and its attribution to sentences, propositions, beliefs or the like. Such an understanding corresponds also to a routine linguistic practice, when one operates with the adjective ‘true’ and asserts, e.g., ‘That 5 is a prime number is true’. By contrast with this apparently quite natural attitude, the suggestion to interpret truth as an object may seem very confusing, to say the least. Nevertheless this suggestion is also equipped with a profound and strong motivation demonstrating that it is far from being just an oddity and has to be taken seriously (cf. Burge 1986).
First, it should be noted that the view of truth as a property is not as natural as it appears on the face of it. Frege brought into play an argument to the effect that characterizing a sentence as true adds nothing new to its content, for ‘It is true that 5 is a prime number’ says exactly the same as just ‘5 is a prime number’. That is, the adjective ‘true’ is in a sense redundant and thus is not a real predicate expressing a real property such as the predicates ‘white’ or ‘prime’ which, on the contrary, cannot simply be eliminated from a sentence without an essential loss for its content. In this case a superficial grammatical analogy is misleading. This idea gave an impetus to the deflationary conception of truth (advocated by Ramsey, Ayer, Quine, Horwich, and others, see the entry on the deflationary theory of truth ).
However, even admitting the redundancy of truth as a property, Frege emphasizes its importance and indispensable role in some other respect. Namely, truth, accompanying every act of judgment as its ultimate goal, secures an objective value of cognition by arranging for every assertive sentence a transition from the level of sense (the thought expressed by a sentence) to the level of denotation (its truth value). This circumstance specifies the significance of taking truth as a particular object. As Tyler Burge explains:
Normally, the point of using sentences, what “matters to us”, is to claim truth for a thought. The object, in the sense of the point or objective , of sentence use was truth. It is illuminating therefore to see truth as an object. (Burge 1986: 120)
As it has been observed repeatedly in the literature (cf., e.g., Burge 1986, Ruffino 2003), the stress Frege laid on the notion of a truth value was, to a great extent, pragmatically motivated. Besides an intended gain for his system of “Basic Laws” (Frege 1893/1903) reflected in enhanced technical clarity, simplicity, and unity, Frege also sought to substantiate in this way his view on logic as a theoretical discipline with truth as its main goal and primary subject-matter. Incidentally, Gottfried Gabriel (1986) demonstrated that in the latter respect Frege’s ideas can be naturally linked up with a value-theoretical tradition in German philosophy of the second half of the 19 th century; see also (Gabriel 2013) on the relation between Frege’s value-theoretically inspired conception of truth values and his theory of judgement. More specifically, Wilhelm Windelband, the founder and the principal representative of the Southwest school of Neo-Kantianism, was actually the first who employed the term “truth value” (“ Wahrheitswert ”) in his essay “What is Philosophy?” published in 1882 (see Windelband 1915: 32), i.e., nine years before Frege 1891, even if he was very far from treating a truth value as a value of a function.
Windelband defined philosophy as a “critical science about universal values”. He considered philosophical statements to be not mere judgements but rather assessments , dealing with some fundamental values, the value of truth being one of the most important among them. This latter value is to be studied by logic as a special philosophical discipline. Thus, from a value-theoretical standpoint, the main task of philosophy, taken generally, is to establish the principles of logical, ethical and aesthetical assessments, and Windelband accordingly highlighted the triad of basic values: “true”, “good” and “beautiful”. Later this triad was taken up by Frege in 1918 when he defined the subject-matter of logic (see below). Gabriel points out (1984: 374) that this connection between logic and a value theory can be traced back to Hermann Lotze, whose seminars in Göttingen were attended by both Windelband and Frege.
The decisive move made by Frege was to bring together a philosophical and a mathematical understanding of values on the basis of a generalization of the notion of a function on numbers. While Frege may have been inspired by Windelband’s use of the word ‘value’ (and even more concretely – ‘truth value’), it is clear that he uses the word in its mathematical sense. If predicates are construed as a kind of functional expressions which, being applied to singular terms as arguments, produce sentences, then the values of the corresponding functions must be references of sentences. Taking into account that the range of any function typically consists of objects, it is natural to conclude that references of sentences must be objects as well. And if one now just takes it that sentences refer to truth values ( the True and the False ), then it turns out that truth values are indeed objects, and it seems quite reasonable to generally explicate truth and falsity as objects and not as properties. As Frege explains:
A statement contains no empty place, and therefore we must take its Bedeutung as an object. But this Bedeutung is a truth-value. Thus the two truth-values are objects. (Frege 1891, trans. Beaney 1997: 140)
Frege’s theory of sentences as names of truth values has been criticized, for example, by Michael Dummett who stated rather dramatically:
This was the most disastrous of the effects of the misbegotten doctrine that sentences are a species of complex singular terms, which dominated Frege’s later period: to rob him of the insight that sentences play a unique role, and that the role of almost every other linguistic expression … consists in its part in forming sentences. (Dummett 1981: 196)
But even Dummett (1991: 242) concedes that “to deny that truth-values are objects … seems a weak response”.
If truth values are accepted and taken seriously as a special kind of objects, the obvious question as to the nature of these entities arises. The above characterization of truth values as objects is far too general and requires further specification. One way of such specification is to qualify truth values as abstract objects. Note that Frege himself never used the word ‘abstract’ when describing truth values. Instead, he has a conception of so called “logical objects”, truth values being primary and the most fundamental of them (Frege 1976: 121). Among the other logical objects Frege pays particular attention to are sets and numbers, emphasizing thus their logical nature (in accordance with his logicist view).
Church (1956: 25), when considering truth values, explicitly attributes to them the property of being abstract. Since then it is customary to label truth values as abstract objects, thus allocating them into the same category of entities as mathematical objects (numbers, classes, geometrical figures) and propositions. One may pose here an interesting question about the correlation between Fregean logical objects and abstract objects in the modern sense (see the entry on abstract objects ). Obviously, the universe of abstract objects is much broader than the universe of logical objects as Frege conceives them. The latter are construed as constituting an ontological foundation for logic, and hence for mathematics (pursuant to Frege’s logicist program). Generally, the class of abstracta includes a wide diversity of platonic universals (such as redness, youngness, justice or triangularity) and not only those of them which are logically necessary. Nevertheless, it may safely be said that logical objects can be considered as paradigmatic cases of abstract entities, or abstract objects in their purest form.
It should be noted that finding an adequate definition of abstract objects is a matter of considerable controversy. According to a common view, abstract entities lack spatio-temporal properties and relations, as opposed to concrete objects which exist in space and time (Lowe 1995: 515). In this respect truth values obviously are abstract as they clearly have nothing to do with physical spacetime. In a similar fashion truth values fulfill another requirement often imposed upon abstract objects, namely the one of a causal inefficacy (see, e.g., Grossmann 1992: 7). Here again, truth values are very much like numbers and geometrical figures: they have no causal power and make nothing happen.
Finally, it is of interest to consider how truth values can be introduced by applying so-called abstraction principles , which are used for supplying abstract objects with criteria of identity . The idea of this method of characterizing abstract objects is also largely due to Frege, who wrote:
If the symbol a is to designate an object for us, then we must have a criterion that decides in all cases whether b is the same as a , even if it is not always in our power to apply this criterion. (Frege 1884, trans. Beaney 1997: 109)
More precisely, one obtains a new object by abstracting it from some given kind of entities, in virtue of certain criteria of identity for this new (abstract) object. This abstraction is performed in terms of an equivalence relation defined on the given entities (see Wrigley 2006: 161). The celebrated slogan by Quine (1969: 23) “No entity without identity” is intended to express essentially the same understanding of an (abstract) object as an “item falling under a sortal concept which supplies a well-defined criterion of identity for its instances” (Lowe 1997: 619).
For truth values such a criterion has been suggested in Anderson and Zalta (2004: 2), stating that for any two sentences \(p\) and \(q\), the truth value of \(p\) is identical with the truth value of \(q\) if and only if \(p\) is (non-logically) equivalent with \(q\) (cf. also Dummett 1959: 141). This idea can be formally explicated following the style of presentation in Lowe (1997: 620):
where &, \(\Rightarrow, \Leftrightarrow, \forall\) stand correspondingly for ‘and’, ‘if… then’, ‘if and only if’ and ‘for all’ in the metalanguage , and \(\leftrightarrow\) stands for some object language equivalence connective (biconditional).
Incidentally, Carnap (1947: 26), when introducing truth-values as extensions of sentences, is guided by essentially the same idea. Namely, he points out a strong analogy between extensions of predicators and truth values of sentences. Carnap considers a wide class of designating expressions (“designators”) among which there are predicate expressions (“predicators”), functional expressions (“functors”), and some others. Applying the well-known technique of interpreting sentences as predicators of degree 0, he generalizes the fact that two predicators of degree \(n\) (say, \(P\) and \(Q)\) have the same extension if and only if \(\forall x_1\forall x_2 \ldots \forall x_n(Px_1 x_2\ldots x_n \leftrightarrow Qx_1 x_2\ldots x_n)\) holds. Then, analogously, two sentences (say, \(p\) and \(q)\), being interpreted as predicators of degree 0, must have the same extension if and only if \(p\leftrightarrow q\) holds, that is if and only if they are equivalent. And then, Carnap remarks, it seems quite natural to take truth values as extensions for sentences.
Note that this criterion employs a functional dependency between an introduced abstract object (in this case a truth value) and some other objects (sentences). More specifically, what is considered is the truth value of a sentence (or proposition, or the like). The criterion of identity for truth values is formulated then through the logical relation of equivalence holding between these other objects—sentences, propositions, or the like (with an explicit quantification over them).
It should also be remarked that the properties of the object language biconditional depend on the logical system in which the biconditional is employed. Biconditionals of different logics may have different logical properties, and it surely matters what kind of the equivalence connective is used for defining truth values. This means that the concept of a truth value introduced by means of the identity criterion that involves a biconditional between sentences is also logic-relative. Thus, if ‘\(\leftrightarrow\)’ stands for material equivalence, one obtains classical truth values, but if the intuitionistic biconditional is employed, one gets truth values of intuitionistic logic, etc. Taking into account the role truth values play in logic, such an outcome seems to be not at all unnatural.
Anderson and Zalta (2004: 13), making use of an object theory from Zalta (1983), propose the following definition of ‘the truth value of proposition \(p\)’ (‘\(tv(p)\)’ [notation adjusted]):
where \(A\)! stands for a primitive theoretical predicate ‘being abstract’, \(xF\) is to be read as “\(x\) encodes \(F\)” and [λ y q ] is a propositional property (“being such a \(y\) that \(q\)”). That is, according to this definition, “the extension of \(p\) is the abstract object that encodes all and only the properties of the form [λ y q ] which are constructed out of propositions \(q\) materially equivalent to \(p\)” (Anderson and Zalta 2004: 14).
The notion of a truth value in general is then defined as an object which is the truth value of some proposition:
Using this apparatus, it is possible to explicitly define the Fregean truth values the True \((\top)\) and the False \((\bot)\):
Anderson and Zalta prove then that \(\top\) and \(\bot\) are indeed truth values and, moreover, that there are exactly two such objects. The latter result is expected, if one bears in mind that what the definitions above actually introduce are the classical truth values (as the underlying logic is classical). Indeed, \(p\leftrightarrow q\) is classically equivalent to \((p\wedge q)\vee(\neg p\wedge \neg q)\), and \(\neg(p\leftrightarrow q)\) is classically equivalent to \((p\wedge \neg q)\vee(\neg p\wedge q)\). That is, the connective of material equivalence divides sentences into two distinct collections. Due to the law of excluded middle these collections are exhaustive, and by virtue of the law of non-contradiction they are exclusive. Thus, we get exactly two equivalence classes of sentences, each being a hypostatized representative of one of two classical truth values.
2. Truth values as logical values
In a late paper Frege (1918) claims that the word ‘true’ determines the subject-matter of logic in exactly the same way as the word ‘beautiful’ does for aesthetics and the word ‘good’ for ethics. Thus, according to such a view, the proper task of logic consists, ultimately, in investigating “the laws of being true” (Sluga 2002: 86). By doing so, logic is interested in truth as such, understood objectively, and not in what is merely taken to be true. Now, if one admits that truth is a specific abstract object (the corresponding truth value), then logic in the first place has to explore the features of this object and its interrelations to other entities of various other kinds.
A prominent adherent of this conception was Jan Łukasiewicz. As he paradigmatically put it:
All true propositions denote one and the same object, namely truth, and all false propositions denote one and the same object, namely falsehood. I consider truth and falsehood to be singular objects in the same sense as the number 2 or 4 is. … Ontologically, truth has its analogue in being, and falsehood, in non-being. The objects denoted by propositions are called logical values . Truth is the positive, and falsehood is the negative logical value. … Logic is the science of objects of a special kind, namely a science of logical values . (Łukasiewicz 1970: 90)
This definition may seem rather unconventional, for logic is usually treated as the science of correct reasoning and valid inference. The latter understanding, however, calls for further justification. This becomes evident, as soon as one asks, on what grounds one should qualify this or that pattern of reasoning as correct or incorrect.
In answering this question, one has to take into account that any valid inference should be based on logical rules which, according to a commonly accepted view, should at least guarantee that in a valid inference the conclusion(s) is (are) true if all the premises are true. Translating this demand into the Fregean terminology, it would mean that in the course of a correct inference the possession of the truth value The True should be preserved from the premises to the conclusion(s). Thus, granting the realistic treatment of truth values adopted by Frege, the understanding of logic as the science of truth values in fact provides logical rules with an ontological justification placing the roots of logic in a certain kind of ideal entities (see Shramko 2014).
These entities constitute a certain uniform domain, which can be viewed as a subdomain of Frege’s so-called “third realm” (the realm of the objective content of thoughts, and generally abstract objects of various kinds, see Frege 1918, cf. Popper 1972 and also Burge 1992: 634). Among the subdomains of this third realm one finds, e.g., the collection of mathematical objects (numbers, classes, etc.). The set of truth values may be regarded as forming another such subdomain, namely the one of logical values , and logic as a branch of science rests essentially on this logical domain and on exploring its features and regularities.
According to Frege, there are exactly two truth values, the True and the False . This opinion appears to be rather restrictive, and one may ask whether it is really indispensable for the concept of a truth value. One should observe that in elaborating this conception, Frege assumed specific requirements of his system of the Begriffsschrift , especially the principle of bivalence taken as a metatheoretical principle, viz. that there exist only two distinct logical values. On the object-language level this principle finds its expression in the famous classical laws of excluded middle and non-contradiction. The further development of modern logic, however, has clearly demonstrated that classical logic is only one particular theory (although maybe a very distinctive one) among the vast variety of logical systems. In fact, the Fregean ontological interpretation of truth values depicts logical principles as a kind of ontological postulations, and as such they may well be modified or even abandoned. For example, by giving up the principle of bivalence, one is naturally led to the idea of postulating many truth values .
It was Łukasiewicz, who as early as 1918 proposed to take seriously other logical values different from truth and falsehood (see Łukasiewicz 1918, 1920). Independently of Łukasiewicz, Emil Post in his dissertation from 1920, published as Post 1921, introduced \(m\)-valued truth tables, where \(m\) is any positive integer. Whereas Post’s interest in many-valued logic (where “many” means “more than two”) was almost exclusively mathematical, Łukasiewicz’s motivation was philosophical (see the entry on many-valued logic ). He contemplated the semantical value of sentences about the contingent future, as discussed in Aristotle’s De interpretatione . Łukasiewicz introduced a third truth value and interpreted it as “possible”. By generalizing this idea and also adopting the above understanding of the subject-matter of logic, one naturally arrives at the representation of particular logical systems as a certain kind of valuation systems (see, e.g., Dummett 1981, 2000; Ryan and Sadler 1992).
Consider a propositional language \(\mathcal{L}\) built upon a set of atomic sentences \(\mathcal{P}\) and a set of propositional connectives \(\mathcal{C}\) (the set of sentences of \(\mathcal{L}\) being the smallest set containing \(\mathcal{P}\) and being closed under the connectives from \(\mathcal{C})\). Then a valuation system \(\mathbf{V}\) for the language \(\mathcal{L}\) is a triple \(\langle \mathcal{V}, \mathcal{D}, \mathcal{F}\rangle\), where \(\mathcal{V}\) is a non-empty set with at least two elements, \(\mathcal{D}\) is a subset of \(\mathcal{V}\), and \(\mathcal{F} = \{f_{c _1},\ldots, f_{c _m}\}\) is a set of functions such that \(f_{c _i}\) is an \(n\)-place function on \(\mathcal{V}\) if \(c_i\) is an \(n\)-place connective. Intuitively, \(\mathcal{V}\) is the set of truth values, \(\mathcal{D}\) is the set of designated truth values, and \(\mathcal{F}\) is the set of truth-value functions interpreting the elements of \(\mathcal{C}\). If the set of truth values of a valuation system \(\mathbf{V}\) has \(n\) elements, \(\mathbf{V}\) is said to be \(n\)-valued. Any valuation system can be equipped with an assignment function which maps the set of atomic sentences into \(\mathcal{V}\). Each assignment \(a\) relative to a valuation system \(\mathbf{V}\) can be extended to all sentences of \(\mathcal{L}\) by means of a valuation function \(v_a\) defined in accordance with the following conditions:
It is interesting to observe that the elements of \(\mathcal{V}\) are sometimes referred to as quasi truth values . Siegfried Gottwald (1989: 2) explains that one reason for using the term ‘quasi truth value’ is that there is no convincing and uniform interpretation of the truth values that in many-valued logic are assumed in addition to the classical truth values the True and the False , an understanding that, according to Gottwald, associates the additional values with the naive understanding of being true, respectively the naive understanding of degrees of being true (cf. also the remark by Font (2009: 383) that “[o]ne of the main problems in many-valued logic, at least in its initial stages, was the interpretation of the ‘intermediate’ or ‘non-classical’ values”, et seq.). In later publications, Gottwald has changed his terminology and states that
[t]o avoid any confusion with the case of classical logic one prefers in many-valued logic to speak of truth degrees and to use the word “truth value” only for classical logic. (Gottwald 2001: 4)
Nevertheless in what follows the term ‘truth values’ will be used even in the context of many-valued logics, without any commitment to a philosophical conception of truth as a graded notion or a specific understanding of semantical values in addition to the classical truth values.
Since the cardinality of \(\mathcal{V}\) may be greater than 2, the notion of a valuation system provides a natural foundational framework for the very idea of a many-valued logic. The set \(\mathcal{D}\) of designated values is of central importance for the notion of a valuation system. This set can be seen as a generalization of the classical truth value the True in the sense that it determines many central logical notions and thereby generalizes some of the important roles played by Frege’s the True (cf. the introductory remarks about uses of truth values). For example, the set of tautologies (logical laws) is directly specified by the given set of designated truth values: a sentence \(A\) is a tautology in a valuation system \(\mathbf{V}\) iff for every assignment \(a\) relative to \(\mathbf{V}\), \(v_a(A) \in \mathcal{D}\). Another fundamental logical notion—that of an entailment relation—can also be defined by referring to the set \(\mathcal{D}\). For a given valuation system \(\mathbf{V}\) a corresponding entailment relation \((\vDash_V)\) is usually defined by postulating the preservation of designated values from the premises to the conclusion:
A pair \(\mathcal{M} = \langle \mathbf{V}, v_a\rangle\), where \(\mathbf{V}\) is an \((n\)-valued) valuation system and \(v_a\) a valuation in \(\mathbf{V}\), may be called an \((n\)-valued) model based on \(\mathbf{V}\). Every model \(\mathcal{M} = \langle \mathbf{V}, v_a\rangle\) comes with a corresponding entailment relation \(\vDash_{\mathcal{M}}\) by defining \(Δ\vDash_{\mathcal{M} }A\textrm{ iff }(\forall B \in Δ: v_a (B) \in \mathcal{D}) \Rightarrow v_a(A) \in \mathcal{D}\).
Suppose \(\mathfrak{L}\) is a syntactically defined logical system \(\mathfrak{L}\) with a consequence relation \(\vdash_{ \mathfrak{L} }\), specified as a relation between the power-set of \(\mathcal{L}\) and \(\mathcal{L}\). Then a valuational system \(\mathbf{V}\) is said to be strictly characteristic for \(\mathfrak{L}\) just in case \(Δ\vDash_V A \textrm{ iff } Δ\vdash_{ \mathfrak{L} }A\) (see Dummett 1981: 431). Conversely, one says that \(\mathfrak{L}\) is characterized by \(\mathbf{V}\). Thus, if a valuation system is said to determine a logic, the valuation system by itself is, properly speaking, not a logic, but only serves as a semantic basis for some logical system. Valuation systems are often referred to as ( logical ) matrices . Note that in Urquhart 1986, the set \(\mathcal{D}\) of designated elements of a matrix is required to be non-empty, and in Dunn & Hardegree 2001, \(\mathcal{D}\) is required to be a non-empty proper subset of \(\mathbf{V}\). With a view on semantically defining a many-valued logic, these restrictions are very natural and have been taken up in Shramko & Wansing 2011 and elsewhere. For the characterization of consequence relations (see the supplementary document Suszko’s Thesis ), however, the restrictions do not apply.
In this way Fregean, i.e., classical, logic can be presented as determined by a particular valuation system based on exactly two elements: \(\mathbf{V}_{cl} = \langle \{T, F\}, \{T\}, \{ f_{\wedge}, f_{\vee}, f_{\rightarrow}, f_{\sim}\}\rangle\), where \(f_{\wedge}, f_{\vee}, f_{\rightarrow},f_{\sim}\) are given by the classical truth tables for conjunction, disjunction, material implication, and negation.
As an example for a valuation system based on more that two elements, consider two well-known valuation systems which determine Kleene’s (strong) “logic of indeterminacy” \(K_3\) and Priest’s “logic of paradox” \(P_3\). In a propositional language without implication, \(K_3\) is specified by the Kleene matrix \(\mathbf{K}_3 = \langle \{T, I, F\}, \{T\}, \{ f_c: c \in \{\sim , \wedge , \vee \}\} \rangle\), where the functions \(f_c\) are defined as follows:
The Priest matrix \(\mathbf{P}_3\) differs from \(\mathbf{K}_3\) only in that \(\mathcal{D} = \{T, I\}\). Entailment in \(\mathbf{K}_3\) as well as in \(\mathbf{P}_3\) is defined by means of ( 3 ).
There are natural intuitive interpretations of \(I\) in \(\mathbf{K}_3\) and in \(\mathbf{P}_3\) as the underdetermined and the overdetermined value respectively—a truth-value gap and a truth-value glut. Formally these interpretations can be modeled by presenting the values as certain subsets of the set of classical truth values \(\{T, F\}\). Then \(T\) turns into \(\mathbf{T} = \{T\}\) (understood as “true only”), \(F\) into \(\mathbf{F} = \{F\}\) (“false only”), \(I\) is interpreted in \(K_3\) as \(\mathbf{N} = \{\} = \varnothing\) (“ neither true nor false”), and in \(P_3\) as \(\mathbf{B} = \{T, F\}\) (“ both true and false”). (Note that also Asenjo (1966) considers the same truth-tables with an interpretation of the third value as “antinomic”.) The designatedness of a truth value can be understood in both cases as containment of the classical \(T\) as a member.
If one combines all these new values into a joint framework, one obtains the four-valued logic \(B_4\) introduced by Dunn and Belnap (Dunn 1976; Belnap 1977a,b). A Gentzen-style formulation can be found in Font (1997: 7)). This logic is determined by the Belnap matrix \(\mathbf{B}_4 = \langle \{\mathbf{N}, \mathbf{T}, \mathbf{F}, \mathbf{B}\}, \{\mathbf{T}, \mathbf{B}\}, \{ f_c: c \in \{\sim , \wedge , \vee \}\}\rangle\), where the functions \(f_c\) are defined as follows:
Definition ( 3 ) applied to the Belnap matrix determines the entailment relation of \(\mathbf{B}_4\). This entailment relation is formalized as the well-known logic of “first-degree entailment” (\(E_{fde}\)) introduced in Anderson & Belnap 1975 (see also Omori and Wansing 2017).
The syntactic notion of a single-conclusion consequence relation has been extensively studied by representatives of the Polish school of logic, most notably by Alfred Tarski, who in fact initiated this line of research (see Tarski 1930a,b; cf. also Wójcicki 1988). In view of certain key features of a standard consequence relation it is quite remarkable—as well as important—that any entailment relation \(\vDash_V\) defined as above has the following structural properties (see Ryan and Sadler 1992: 34):
Moreover, for every \(A \in \mathcal{L}\), every \(Δ \subseteq \mathcal{L}\), and every uniform substitution function \(σ\) on \(\mathcal{L}\) the following Substitution property holds (\(σ(Δ)\) stands for \(\{ σ(B) \mid B \in Δ\})\):
(The function of uniform substitution \(σ\) is defined as follows. Let \(B\) be a formula in \(\mathcal{L}\), let \(p_1,\ldots, p_n\) be all the propositional variables occurring in \(B\), and let \(σ(p_1) = A_1,\ldots , σ(p_n) = A_n\) for some formulas \(A_1 ,\ldots ,A_n\). Then \(σ(B)\) is the formula that results from B by substituting simultaneously \(A_1\),…, \(A_n\) for all occurrences of \(p_1,\ldots, p_n\), respectively.)
If \(\vDash_V\) in the conditions (4)–(6) is replaced by \(\vdash_{ \mathfrak{L} }\), then one obtains what is often called a Tarskian consequence relation . If additionally a consequence relation has the substitution property ( 7 ), then it is called structural . Thus, any entailment relation defined for a given valuation system \(\mathbf{V}\) presents an important example of a consequence relation, in that \(\mathbf{V}\) is strictly characteristic for some logical system \(\mathfrak{L}\) with a structural Tarskian consequence relation.
Generally speaking, the framework of valuation systems not only perfectly suits the conception of logic as the science of truth values, but also turns out to be an effective technical tool for resolving various sophisticated and important problems in modern logic, such as soundness, completeness, independence of axioms, etc.
The term ‘truth degrees’, used by Gottwald and many other authors, suggests that truth comes by degrees, and these degrees may be seen as truth values in an extended sense. The idea of truth as a graded notion has been applied to model vague predicates and to obtain a solution to the Sorites Paradox, the Paradox of the Heap (see the entry on the Sorites Paradox ). However, the success of applying many-valued logic to the problem of vagueness is highly controversial. Timothy Williamson (1994: 97), for example, holds that the phenomenon of higher-order vagueness “makes most work on many-valued logic irrelevant to the problem of vagueness”.
In any case, the vagueness of concepts has been much debated in philosophy (see the entry on vagueness ) and it was one of the major motivations for the development of fuzzy logic (see the entry on fuzzy logic ). In the 1960s, Lotfi Zadeh (1965) introduced the notion of a fuzzy set . A characteristic function of a set \(X\) is a mapping which is defined on a superset \(Y\) of \(X\) and which indicates membership of an element in \(X\). The range of the characteristic function of a classical set \(X\) is the two-element set \(\{0,1\}\) (which may be seen as the set of classical truth values). The function assigns the value 1 to elements of \(X\) and the value 0 to all elements of \(Y\) not in \(X\). A fuzzy set has a membership function ranging over the real interval [0,1]. A vague predicate such as ‘is much earlier than March 20 th , 1963’, ‘is beautiful’, or ‘is a heap’ may then be regarded as denoting a fuzzy set. The membership function \(g\) of the fuzzy set denoted by ‘is much earlier than March 20 th , 1963’ thus assigns values (seen as truth degrees) from the interval [0, 1] to moments in time, for example \(g\)(1p.m., August 1 st , 2006) \(= 0\), \(g\)(3a.m., March 19 th , 1963) \(= 0\), \(g\)(9:16a.m., April 9 th , 1960) \(= 0.005\), \(g\)(2p.m., August 13 th , 1943) \(= 0.05\), \(g\)(7:02a.m., December 2 nd , 1278) \(= 1\).
The application of continuum-valued logics to the Sorites Paradox has been suggested by Joseph Goguen (1969). The Sorites Paradox in its so-called conditional form is obtained by repeatedly applying modus ponens in arguments such as:
- A collection of 100,000 grains of sand is a heap.
- If a collection of 100,000 grains of sand is a heap, then a collection 99,999 grains of sand is a heap.
- If a collection of 99,999 grains of sand is a heap, then a collection 99,998 grains of sand is a heap.
- If a collection of 2 grains of sand is a heap, then a collection of 1 grain of sand is a heap.
- Therefore: A collection of 1 grain of sand is a heap.
Whereas it seems that all premises are acceptable, because the first premise is true and one grain does not make a difference to a collection of grains being a heap or not, the conclusion is, of course, unacceptable. If the predicate ‘is a heap’ denotes a fuzzy set and the conditional is interpreted as implication in Łukasiewicz’s continuum-valued logic, then the Sorites Paradox can be avoided. The truth-function \(f_{\rightarrow}\) of Łukasiewicz’s implication \(\rightarrow\) is defined by stipulating that if \(x \le y\), then \(f_{\rightarrow}(x, y) = 1\), and otherwise \(f_{\rightarrow}(x, y) = 1 - (x - y)\). If, say, the truth value of the sentence ‘A collection of 500 grains of sand is a heap’ is 0.8 and the truth value of ‘A collection of 499 grains of sand is a heap’ is 0.7, then the truth value of the implication ‘If a collection of 500 grains of sand is a heap, then a collection 499 grains of sand is a heap.’ is 0.9. Moreover, if the acceptability of a statement is defined as having a value greater than \(j\) for \(0 \lt j \lt 1\) and all the conditional premises of the Sorites Paradox do not fall below the value \(j\), then modus ponens does not preserve acceptability, because the conclusion of the Sorites Argument, being evaluated as 0, is unacceptable.
Alasdair Urquhart (1986: 108) stresses
the extremely artificial nature of the attaching of precise numerical values to sentences like … “Picasso’s Guernica is beautiful”.
To overcome the problem of assigning precise values to predications of vague concepts, Zadeh (1975) introduced fuzzy truth values as distinct from the numerical truth values in [0, 1], the former being fuzzy subsets of the set [0, 1], understood as true , very true , not very true , etc.
The interpretation of continuum-valued logics in terms of fuzzy set theory has for some time be seen as defining the field of mathematical fuzzy logic. Susan Haack (1996) refers to such systems of mathematical fuzzy logic as “base logics” of fuzzy logic and reserves the term ‘fuzzy logics’ for systems in which the truth values themselves are fuzzy sets. Fuzzy logic in Zadeh’s latter sense has been thoroughly criticized from a philosophical point of view by Haack (1996) for its “methodological extravagances” and its linguistic incorrectness. Haack emphasizes that her criticisms of fuzzy logic do not apply to the base logics. Moreover, it should be pointed out that mathematical fuzzy logics are nowadays studied not in the first place as continuum-valued logics, but as many-valued logics related to residuated lattices (see Hajek 1998; Cignoli et al. 2000; Gottwald 2001; Galatos et al. 2007), whereas fuzzy logic in the broad sense is to a large extent concerned with certain engineering methods.
A fundamental concern about the semantical treatment of vague predicates is whether an adequate semantics should be truth-functional, that is, whether the truth value of a complex formula should depend functionally on the truth values of its subformulas. Whereas mathematical fuzzy logic is truth-functional, Williamson (1994: 97) holds that “the nature of vagueness is not captured by any approach that generalizes truth-functionality”. According to Williamson, the degree of truth of a conjunction, a disjunction, or a conditional just fails to be a function of the degrees of truth of vague component sentences. The sentences ‘John is awake’ and ‘John is asleep’, for example, may have the same degree of truth. By truth-functionality the sentences ‘If John is awake, then John is awake’ and ‘If John is awake, then John is asleep’ are alike in truth degree, indicating for Williamson the failure of degree-functionality.
One way of in a certain sense non-truthfunctionally reasoning about vagueness is supervaluationism. The method of supervaluations has been developed by Henryk Mehlberg (1958) and Bas van Fraassen (1966) and has later been applied to vagueness by Kit Fine (1975), Rosanna Keefe (2000) and others.
Van Fraassen’s aim was to develop a semantics for sentences containing non-denoting singular terms. Even if one grants atomic sentences containing non-denoting singular terms and that some attributions of vague predicates are neither true nor false, it nevertheless seems natural not to preclude that compound sentences of a certain shape containing non-denoting terms or vague predications are either true or false, e.g., sentences of the form ‘If \(A\), then \(A\)’. Supervaluational semantics provides a solution to this problem. A three-valued assignment \(a\) into \(\{T, I, F\}\) may assign a truth-value gap (or rather the value \(I)\) to the vague sentence ‘Picasso’s Guernica is beautiful’. Any classical assignment \(a'\) that agrees with \(a\) whenever \(a\) assigns \(T\) or \(F\) may be seen as a precisification (or superassignment) of \(a\). A sentence may than be said to be supertrue under assignment \(a\) if it is true under every precisification \(a'\) of \(a\). Thus, if \(a\) is a three-valued assignment into \(\{T, I, F\}\) and \(a'\) is a two-valued assignment into \(\{T, F\}\) such that \(a(p) = a'(p)\) if \(a(p) \in \{T, F\}\), then \(a'\) is said to be a superassignment of \(a\). It turns out that if \(a\) is an assignment extended to a valuation function \(v_a\) for the Kleene matrix \(\mathbf{K}_3\), then for every formula \(A\) in the language of \(\mathbf{K}_3\), \(v_a (A) = v_{a'}(A)\) if \(v_a (A) \in \{T, F\}\). Therefore, the function \(v_{a'}\) may be called a supervaluation of \(v_a\). A formula is then said to be supertrue under a valuation function \(v_a\) for \(\mathbf{K}_3\) if it is true under every supervaluation \(v_{a'}\) of \(v_a\), i.e., if \(v_{a'}(A) = T\) for every supervaluation \(v_{a'}\) of \(v_a\). The property of being superfalse is defined analogously.
Since every supervaluation is a classical valuation, every classical tautology is supertrue under every valuation function in \(\mathbf{K}_3\). Supervaluationism is, however, not truth-functional with respect to supervalues. The supervalue of a disjunction, for example, does not depend on the supervalue of the disjuncts. Suppose \(a(p) = I\). Then \(a(\neg p) = I\) and \(v_{a'} (p\vee \neg p) = T\) for every supervaluation \(v_{a'}\) of \(v_a\). Whereas \((p\vee \neg p)\) is thus supertrue under \(v_a,p\vee p\) is not , because there are superassignments \(a'\) of \(a\) with \(a'(p) = F\). An argument against the charge that supervaluationism requires a non-truth-functional semantics of the connectives can be found in MacFarlane (2008) (cf. also other references given there).
Although the possession of supertruth is preserved from the premises to the conclusion(s) of valid inferences in supervaluationism, and although it might be tempting to consider supertruth an abstract object on its own, it seems that it has never been suggested to hypostatize supertruth in this way, comparable to Frege’s the True . A sentence supertrue under a three-valued valuation \(v\) just takes the Fregean value the True under every supervaluation of \(v\). The advice not to confuse supertruth with “real truth” can be found in Belnap (2009).
2.4 Suszko’s thesis and anti-designated values
One might, perhaps, think that the mere existence of many-valued logics shows that there exist infinitely, in fact, uncountably many truth values. However, this is not at all clear (recall the more cautious use of terminology advocated by Gottwald).
In the 1970’s Roman Suszko (1977: 377) declared many-valued logic to be “a magnificent conceptual deceit”. Suszko actually claimed that “there are but two logical values, true and false” (Caleiro et al . 2005: 169), a statement now called Suszko’s Thesis . For Suszko, the set of truth values assumed in a logical matrix for a many-valued logic is a set of “admissible referents” (called “algebraic values”) of formulas but not a set of logical values. Whereas the algebraic values are elements of an algebraic structure and referents of formulas, the logical value true is used to define valid consequence: If every premise is true, then so is (at least one of) the conclusion(s). The other logical value, false , is preserved in the opposite direction: If the (every) conclusion is false, then so is at least one of the premises. The logical values are thus represented by a bi-partition of the set of algebraic values into a set of designated values (truth) and its complement (falsity).
Essentially the same idea has been taken up earlier by Dummett (1959) in an influential paper, where he asks
what point there may be in distinguishing between different ways in which a statement may be true or between different ways in which it may be false, or, as we might say, between degrees of truth and falsity. (Dummett 1959: 153)
Dummett observes that, first,
the sense of a sentence is determined wholly by knowing the case in which it has a designated value and the cases in which it has an undesignated one,
and moreover,
finer distinctions between different designated values or different undesignated ones, however naturally they come to us, are justified only if they are needed in order to give a truth-functional account of the formation of complex statements by means of operators. (Dummett 1959: 155)
Suszko’s claim evidently echoes this observation by Dummett.
Suszko’s Thesis is substantiated by a rigorous proof (the Suszko Reduction) showing that every structural Tarskian consequence relation and therefore also every structural Tarskian many-valued propositional logic is characterized by a bivalent semantics. (Note also that Richard Routley (1975) has shown that every logic based on a λ-categorical language has a sound and complete bivalent possible worlds semantics.) The dichotomy between designated values and values which are not designated and its use in the definition of entailment plays a crucial role in the Suszko Reduction. Nevertheless, while it seems quite natural to construe the set of designated values as a generalization of the classical truth value \(T\) in some of its significant roles, it would not always be adequate to interpret the set of non-designated values as a generalization of the classical truth value \(F\). The point is that in a many-valued logic, unlike in classical logic, “not true” does not always mean “false” (cf., e.g., the above interpretation of Kleene’s logic, where sentences can be neither true nor false).
In the literature on many-valued logic it is sometimes proposed to consider a set of antidesignated values which not obligatorily constitute the complement of the set of designated values (see, e.g., Rescher 1969, Gottwald 2001). The set of antidesignated values can be regarded as representing a generalized concept of falsity. This distinction leaves room for values that are neither designated nor antidesignated and even for values that are both designated and antidesignated.
Grzegorz Malinowski (1990, 1994) takes advantage of this proposal to give a counterexample to Suszko’s Thesis. He defines the notion of a single-conclusion quasi -consequence \((q\)-consequence) relation. The semantic counterpart of \(q\)-consequence is called \(q\)-entailment. Single-conclusion \(q\)-entailment is defined by requiring that if no premise is antidesignated, the conclusion is designated. Malinowski (1990) proved that for every structural \(q\)-consequence relation, there exists a characterizing class of \(q\)-matrices, matrices which in addition to a subset \(\mathcal{D}^{+}\) of designated values comprise a disjoint subset \(\mathcal{D}^-\) of antidesignated values. Not every \(q\)-consequence relation has a bivalent semantics.
In the supplementary document Suszko’s Thesis , Suszko’s reduction is introduced, Malinowski’s counterexample to Suszko’s Thesis is outlined, and a short analysis of these results is presented.
Can one provide evidence for a multiplicity of logical values? More concretely, \(is\) there more than one logical value, each of which may be taken to determine its own (independent) entailment relation? A positive answer to this question emerges from considerations on truth values as structured entities which, by virtue of their internal structure, give rise to natural partial orderings on the set of values.
3. Ordering relations between truth-values
As soon as one admits that truth values come with valuation systems , it is quite natural to assume that the elements of such a system are somehow interrelated . And indeed, already the valuation system for classical logic constitutes a well-known algebraic structure, namely the two-element Boolean algebra with \(\cap\) and \(\cup\) as meet and join operators (see the entry on the mathematics of Boolean algebra ). In its turn, this Boolean algebra forms a lattice with a partial order defined by \(a\le_t b \textrm{ iff } a\cap b = a\). This lattice may be referred to as TWO . It is easy to see that the elements of TWO are ordered as follows: \(F\le_t T\). This ordering is sometimes called the truth order (as indicated by the corresponding subscript), for intuitively it expresses an increase in truth: \(F\) is “less true” than \(T\). It can be schematically presented by means of a so-called Hasse-diagram as in Figure 1.
![what is a truth assignment [a horizontal line segment with the left endpoint labeled 'F' and the right endpoint labeled 'T', below an arrow goes from left to right with the arrowhead labeled 't'.]](https://plato.stanford.edu/Figure1.png)
Figure 1: Lattice TWO
It is also well-known that the truth values of both Kleene’s and Priest’s logic can be ordered to form a lattice ( THREE ), which is diagrammed in Figure 2.
![what is a truth assignment [The same as figure 1 except the line segment has a point near the middle labeled 'I'.]](https://plato.stanford.edu/Figure2.png)
Figure 2: Lattice THREE
Here \(\le_t\) orders \(T, I\) and \(F\) so that the intermediate value \(I\) is “more true” than \(F\), but “less true” than \(T\).
The relation \(\le_t\) is also called a logical order , because it can be used to determine key logical notions: logical connectives and an entailment relation. Namely, if the elements of the given valuation system \(\mathbf{V}\) form a lattice, then the operations of meet and join with respect to \(\le_t\) are usually seen as the functions for conjunction and disjunction, whereas negation can be represented by the inversion of this order. Moreover, one can consider an entailment relation for \(\mathbf{V}\) as expressing agreement with the truth order, that is, the conclusion should be at least as true as the premises taken together:
where \(\Pi_t\) is the lattice meet in the corresponding lattice.
The Belnap matrix \(\mathbf{B}_4\) considered above also can be represented as a partially ordered valuation system. The set of truth values \(\{\mathbf{N}, \mathbf{T}, \mathbf{F}, \mathbf{B}\}\) from \(\mathbf{B}_4\) constitutes a specific algebraic structure – the bilattice FOUR\(_2\) presented in Figure 3 (see, e.g., Ginsberg 1988, Arieli and Avron 1996, Fitting 2006).
![what is a truth assignment [a graph with the y axis labeled 'i' and the x axis labeled 't'. A square with the corners labeled 'B' (top), 'T' (right), 'N' (bottom), and 'F' (left).]](https://plato.stanford.edu/Figure3.png)
Figure 3: The bilattice FOUR \(_2\)
This bilattice is equipped with two partial orderings; in addition to a truth order, there is an information order \((\le_i )\) which is said to order the values under consideration according to the information they give concerning a formula to which they are assigned. Lattice meet and join with respect to \(\le_t\) coincide with the functions \(f_{\wedge}\) and \(f_{\vee}\) in the Belnap matrix \(\mathbf{B}_4\), \(f_{{\sim}}\) turns out to be the truth order inversion, and an entailment relation, which happens to coincide with the matrix entailment, is defined by ( 8 ). FOUR \(_2\) arises as a combination of two structures: the approximation lattice \(A_4\) and the logical lattice \(L_4\) which are discussed in Belnap 1977a and 1977b (see also, Anderson, Belnap and Dunn 1992: 510–518)).
3.2 Truth values as structured entities. Generalized truth values
Frege (1892: 30) points out the possibility of “distinctions of parts within truth values”. Although he immediately specifies that the word ‘part’ is used here “in a special sense”, the basic idea seems nevertheless to be that truth values are not something amorphous, but possess some inner structure. It is not quite clear how serious Frege is about this view, but it seems to suggest that truth values may well be interpreted as complex, structured entities that can be divided into parts.
There exist several approaches to semantic constructions where truth values are represented as being made up from some primitive components. For example, in some explications of Kripke models for intuitionistic logic propositions (identified with sets of “worlds” in a model structure) can be understood as truth values of a certain kind. Then the empty proposition is interpreted as the value false , and the maximal proposition (the set of all worlds in a structure) as the value true . Moreover, one can consider non-empty subsets of the maximal proposition as intermediate truth values. Clearly, the intuitionistic truth values so conceived are composed from some simpler elements and as such they turn out to be complex entities.
Another prominent example of structured truth values are the “truth-value objects” in topos models from category theory (see the entry on category theory ). For any topos \(C\) and for a \(C\)-object Ω one can define a truth value of \(C\) as an arrow \(1 \rightarrow Ω\) (“a subobject classifier for \(C\)”), where 1 is a terminal object in \(C\) (cf. Goldblatt 2006: 81, 94). The set of truth values so defined plays a special role in the logical structure of \(C\), since arrows of the form \(1 \rightarrow Ω\) determine central semantical notions for the given topos. And again, these truth values evidently have some inner structure.
One can also mention in this respect the so-called “factor semantics” for many-valued logic, where truth values are defined as ordered \(n\)-tuples of classical truth values \((T\)-\(F\) sequences, see Karpenko 1983). Then the value \(3/5\), for example, can be interpreted as a \(T\)-\(F\) sequence of length 5 with exactly 3 occurrences of \(T\). Here the classical values \(T\) and \(F\) are used as “building blocks” for non-classical truth values.
Moreover, the idea of truth values as compound entities nicely conforms with the modeling of truth values considered above in three-valued (Kleene, Priest) and four-valued (Belnap) logics as certain subsets of the set of classical truth values. The latter approach stems essentially from Dunn (1976), where a generalization of the notion of a classical truth-value function has been proposed to obtain so-called “underdetermined” and “overdetermined” valuations. Namely, Dunn considers a valuation to be a function not from sentences to elements of the set \(\{T, F\}\) but from sentences to subsets of this set (see also Dunn 2000: 7). By developing this idea, one arrives at the concept of a generalized truth value function , which is a function from sentences into the subsets of some basic set of truth values (see Shramko and Wansing 2005). The values of generalized truth value functions can be called generalized truth values .
By employing the idea of generalized truth value functions, one can obtain a hierarchy of valuation systems starting with a certain set-theoretic representation of the valuation system for classical logic. The representation in question is built on a single initial value which serves then as the designated value of the resulting valuation system. More specifically, consider the singleton \(\{\varnothing \}\) taken as the basic set subject to a further generalization procedure. Set-theoretically the basic set can serve as the universal set (the complement of the empty set) for the valuation system \(\mathbf{V}^{\varnothing}_{cl}\) introduced below. At the first stage \(\varnothing\) comes out with no specific intuitive interpretation, it is only important to take it as some distinct unit . Consider then the power-set of \(\{\varnothing \}\) consisting of exactly two elements: \(\{\{\varnothing \}, \varnothing \}\). Now, these elements can be interpreted as Frege’s the True and the False , and thus it is possible to construct a valuation system for classical logic, \(\mathbf{V}^{\varnothing}_{cl} = \langle \{\{\varnothing \}, \varnothing \}, \{\{\varnothing \}\}, \{f_{\wedge}, f_{\vee}, f_{\rightarrow}, f_{\sim}\}\rangle\), where the functions \(f_{\wedge}, f_{\vee}, f_{\rightarrow}, f_{\sim}\) are defined as follows (for \[ \begin{align} X, Y \in \{\{\varnothing \}, \varnothing \}:\quad & f_{\wedge}(X, Y) = X\cap Y; \\ & f_{\vee}(X, Y) = X\cup Y; \\ & f_{\rightarrow}(X, Y) = X^{c}\cup Y; \\ & f_{\sim}(X) = X^{c}. \end{align} \] It is not difficult to see that for any assignment \(a\) relative to \(\mathbf{V}^{\varnothing}_{cl}\), and for any formulas \(A\) and \(B\), the following holds:
This shows that \(f_{\wedge}, f_{\vee}, f_{\rightarrow}\) and \(f_{\sim}\) determine exactly the propositional connectives of classical logic. One can conveniently mark the elements \(\{\varnothing \}\) and \(\varnothing\) in the valuation system \(\mathbf{V}^{\varnothing}_{cl}\) by the classical labels \(T\) and \(F\). Note that within \(\mathbf{V}^{\varnothing}_{cl}\) it is fully justifiable to associate \(\varnothing\) with falsity, taking into account the virtual monism of truth characteristic for classical logic, which treats falsity not as an independent entity but merely as the absence of truth.
Then, by taking the set \(\mathbf{2} = \{F, T\}\) of these classical values as the basic set for the next valuation system, one obtains the four truth values of Belnap’s logic as the power-set of the set of classical values \(\mathcal{P}(\mathbf{2}) = \mathbf{4}: \mathbf{N} = \varnothing\), \(\mathbf{F} = \{F\} (= \{\varnothing \})\), \(\mathbf{T} = \{T\} (= \{\{\varnothing \}\})\) and \(\mathbf{B} = \{F, T\} (= \{\varnothing, \{\varnothing \}\})\). In this way, Belnap’s four-valued logic emerges as a certain generalization of classical logic with its two Fregean truth values. In Belnap’s logic truth and falsity are considered to be full-fledged, self-sufficient entities, and therefore \(\varnothing\) is now to be interpreted not as falsity, but as a real truth-value gap ( neither true nor false). The dissimilarity of Belnap’s truth and falsity from their classical analogues is naturally expressed by passing from the corresponding classical values to their singleton-sets, indicating thus their new interpretations as false only and true only . Belnap’s interpretation of the four truth values has been critically discussed in Lewis 1982 and Dubois 2008 (see also the reply to Dubois in Wansing and Belnap 2010).
Generalized truth values have a strong intuitive background, especially as a tool for the rational explication of incomplete and inconsistent information states. In particular, Belnap’s heuristic interpretation of truth values as information that “has been told to a computer” (see Belnap 1977a,b; also reproduced in Anderson, Belnap and Dunn 1992, §81) has been widely acknowledged. As Belnap points out, a computer may receive data from various (maybe independent) sources. Belnap’s computers have to take into account various kinds of information concerning a given sentence. Besides the standard (classical) cases, when a computer obtains information either that the sentence is (1) true or that it is (2) false, two other (non-standard) situations are possible: (3) nothing is told about the sentence or (4) the sources supply inconsistent information, information that the sentence is true and information that it is false. And the four truth values from \(\mathbf{B}_4\) naturally correspond to these four situations: there is no information that the sentence is false and no information that it is true \((\mathbf{N})\), there is merely information that the sentence is false \((\mathbf{F})\), there is merely information that the sentence is true \((\mathbf{T})\), and there is information that the sentence is false, but there is also information that it is true \((\mathbf{B})\).
Joseph Camp in 2002: 125–160 provides Belnap’s four values with quite a different intuitive motivation by developing what he calls a “semantics of confused thought”. Consider a rational agent, who happens to mix up two very similar objects (say, \(a\) and \(b)\) and ambiguously uses one name (say, ‘\(C\)’) for both of them. Now let such an agent assert some statement, saying, for instance, that \(C\) has some property. How should one evaluate this statement if \(a\) has the property in question whereas \(b\) lacks it? Camp argues against ascribing truth values to such statements and puts forward an “epistemic semantics” in terms of “profitability” and “costliness” as suitable characterizations of sentences. A sentence \(S\) is said to be “profitable” if one would profit from acting on the belief that \(S\), and it is said to be “costly” if acting on the belief that \(S\) would generate costs, for example as measured by failure to achieve an intended goal. If our “confused agent” asks some external observers whether \(C\) has the discussed property, the following four answers are possible: ‘yes’ (mark the corresponding sentence with \(\mathbf{Y})\), ‘no’ (mark it with \(\mathbf{N})\), ‘cannot say’ (mark it with ? ), ‘yes’ and ‘no’ (mark it with Y&N ). Note that the external observers, who provide answers, are “non-confused” and have different objects in mind as to the referent of ‘\(C\)’, in view of all the facts that may be relevant here. Camp conceives these four possible answers concerning epistemic properties of sentences as a kind of “semantic values”, interpreting them as follows: the value \(\mathbf{Y}\) is an indicator of profitability, the value \(\mathbf{N}\) is an indicator of costliness, the value ? is no indicator either way, and the value Y&N is both an indicator of profitability and an indicator of costliness. A strict analogy between this “semantics of confused reasoning” and Belnap’s four valued logic is straightforward. And indeed, as Camp (2002: 157) observes, the set of implications valid according to his semantics is exactly the set of implications of the entailment system \(E_{fde}\). In Zaitsev and Shramko 2013 it is demonstrated how ontological and epistemic aspects of truth values can be combined within a joint semantical framework. Kapsner (2019) extends Belnap’s framework by two additional values “Contestedly-True” and “Contestedly-False” which allows for new outcomes for disjunctions and conjunctions between statements with values \(\mathbf{B}\) and \(\mathbf{N}\).
The conception of generalized truth values has its purely logical import as well. If one continues the construction and applies the idea of generalized truth value functions to Belnap’s four truth values, then one obtains further valuation systems which can be represented by various multilattices . One arrives, in particular, at SIXTEEN \(_3\) – the trilattice of 16 truth-values, which can be viewed as a basis for a logic of computer networks (see Shramko and Wansing 2005, 2006; Kamide and Wansing 2009; Odintsov 2009; Wansing 2010; Odintsov and Wansing 2015; cf. also Shramko, Dunn, Takenaka 2001). The notion of a multilattice and SIXTEEN \(_3\) are discussed further in the supplementary document Generalized truth values and multilattices . A comprehensive study of the conception of generalized logical values can be found in Shramko and Wansing 2011.
Gottlob Frege’s notion of a truth value has become part of the standard philosophical and logical terminology. The notion of a truth value is an indispensable instrument of realistic, model-theoretic approaches to semantics. Indeed, truth values play an essential role in applications of model-theoretic semantics in areas such as, for example, knowledge representation and theorem proving based on semantic tableaux, which could not be treated in the present entry. Moreover, considerations on truth values give rise to deep ontological questions concerning their own nature, the feasibility of fact ontologies, and the role of truth values in such ontological theories. There also exist well-motivated theories of generalized truth values that lead far beyond Frege’s classical values the True and the False . (For various directions of further logical and philosophical investigations in the area of truth values see Shramko & Wansing 2009b, 2009c.)
- Anderson, Alan R. and Nuel D. Belnap, 1975, Entailment: The Logic of Relevance and Necessity (Volume I), Princeton, NJ: Princeton University Press.
- Anderson, Alan R., Nuel D. Belnap, and J. Michael Dunn, 1992, Entailment: The Logic of Relevance and Necessity , Vol. II, Princeton, NJ: Princeton University Press.
- Anderson, David and Edward Zalta, 2004, “Frege, Boolos, and logical objects”, Journal of Philosophical Logic , 33: 1–26.
- Arieli, Ofer and Arnon Avron, 1996, “Reasoning with logical bilattices”, Journal of Logic, Language and Information , 5: 25–63.
- Asenjo, Florencio G., 1966, “A calculus of antinomies”, Notre Dame Journal of Formal Logic , 7: 103–105.
- Barrio, Eduardo, Lucas, Rosenblatt, and Diego Tajer, 2015, “The logics of strict-tolerant logic”, Journal of Philosophical Logic , 44: 551–571.
- Barrio, Eduardo, Federico, Pailos, and Damian Szmuc, 2020, “A hierarchy of classical and paraconsistent logics”, Journal of Philosophical Logic , 49: 93–120.
- Barwise, Jon and John Perry, 1981, “Semantic innocence and uncompromising situations”, Midwest Studies in the Philosophy of Language , VI: 387–403.
- Beall, Jc and Caleb Camrud, 2020, “A note on FDE “All the way up”, Notre Dame Journal of Formal Logic , 61: 283–296.
- Beaney, Michael (ed. and transl.), 1997, The Frege Reader , Oxford: Wiley-Blackwell.
- Belnap, Nuel D., 1977a, “How a computer should think”, in G. Ryle (ed.), Contemporary Aspects of Philosophy , Stocksfield: Oriel Press Ltd., 30–55.
- –––, 1977b, “A useful four-valued logic”, in J.M. Dunn and G. Epstein (eds.), Modern Uses of Multiple-Valued Logic , Dordrecht: D. Reidel Publishing Co., 8–37.
- –––, 2009, “Truth values, neither-true-nor-false, and supervaluations”, Studia Logica , 91: 305–334.
- Bennett, Jonathan, 1988, Events and their Names . New York: Hackett.
- Béziau, Jean-Yves, 2012, “A History of Truth-Values”, in D. Gabbay et al. (eds.), Handbook of the History of Logic. Vol. 11, Logic: A History of its Central Concepts , Amsterdam: North-Holland, 235–307.
- Blasio, Carolina, João, Marcos, and Heinrich Wansing, 2017, “An inferentially many-valued two-dimensional notion of entailment”, Bulletin of the Section of Logic , 46: 233–262.
- Brown, Bryson and Peter Schotch, 1999, “Logic and aggregation”, Journal of Philosophical Logic , 28: 265–287.
- Burge, Tyler, 1986, “Frege on truth”, in L. Haaparanta and J. Hintikka (eds.), Frege Synthesized , Dordrecht: D. Reidel Publishing Co., 97–154.
- –––, 1992, “Frege on knowing the Third Realm”, Mind , 101: 633–650.
- Caleiro, Carlos, Walter Carnielli, Marcelo Coniglio, and João Marcos, 2005, “Two’s company: ‘The humbug of many logical values’”, in J.-Y. Béziau (ed.), Logica Universalis , Basel: Birkhäuser Verlag, 169–189.
- Camp, Joseph L., 2002, Confusion: A Study in the Theory of Knowledge , Cambridge, MA: Harvard University Press.
- Carnap, Rudolf, 1942, Introduction to Semantics , Cambridge, MA: Harvard University Press.
- –––, 1947, Meaning and Necessity. A Study in Semantics and Modal Logic , Chicago: University of Chicago Press.
- Chemla, Emmanuel and Paul Égré, 2019, “Suszko's problem: Mixed consequence and compositionality”, Review of Symbolic Logic , 12: 736–767.
- Church, Alonzo, 1943, “Review of Rudolf Carnap, Introduction to Semantics ”, The Philosophical Review , 52: 298–304.
- –––, 1956, Introduction to Mathematical Logic , Vol. I, Princeton: Princeton University Press.
- Cignoli, Roberto, Itala D’Ottaviano, and Daniele Mundici, 2000, Algebraic Foundations of Many-valued Reasoning , Dordrecht: Kluwer Academic Publishers.
- Cobreros, Pablo, Égré, Paul, Ripley, David, and Robert van Rooij, 2012, “Tolerant, classical, strict”, Journal of Philosophical Logic , 41: 347–385.
- da Costa, Newton, Jean-Yves Béziau, and Otávio Bueno, 1996, “Malinowski and Suszko on many-valued logics: on the reduction of many-valuedness to two-valuedness”, Modern Logic , 6: 272–299.
- Czelakowski, Janusz, 2001, Protoalgebraic Logics , Dordrecht: Kluwer Academic Publishers.
- Davidson, David, 1967, “Truth and meaning”, Synthese , 17: 304–323.
- –––, 1969, “True to the facts”, Journal of Philosophy , 66: 748–764.
- Deutsch, Harry, 1984, “Paraconsistent analytic implication”, Journal of Philosophical Logic , 13: 1–11.
- Dubois, Didier, 2008, “On ignorance and contradiction considered as truth-values”, Logic Journal of the IGPL , 16: 195–216.
- Dummett, Michael, 1959, “Truth”, in Proceedings of the Aristotelian Society , 59: 141–162 (Reprinted in Truth and Other Enigmas , Cambridge, MA: Harvard University Press, 1978, 1–24).
- –––, 1981, Frege: Philosophy of Language , 2 nd edition, London: Duckworth Publishers.
- –––, 1991, Frege and Other Philosophers , Oxford: Oxford University Press.
- –––, 2000, Elements of Intuitionism , 2 nd ed., Oxford: Clarendon Press.
- Dunn, J. Michael, 1976, “Intuitive semantics for first-degree entailment and ‘coupled trees’”, Philosophical Studies , 29: 149–168.
- –––, 2000, “Partiality and its dual”, Studia Logica , 66: 5–40.
- Dunn, J. Michael and Gary M. Hardegree, 2001, Algebraic Methods in Philosophical Logic (Oxford Logic Guides, Volume 41), Oxford: Science Publications.
- Ferguson, Thomas Macaulay, 2017, Meaning and Proscription in Formal Logic. Variations on the Propositional Logic of William T. Parry (Trends in Logic: Volume 49), Berlin: Springer, 2017.
- Fine, Kit, 1975, “Vagueness, truth and logic”, Synthese , 30: 265–300.
- Fitting, Melvin, 2006, “Bilattices are nice things”, in T. Bolander, V. Hendricks, and S.A. Pedersen (eds.), Self-Reference , Stanford: CSLI Publications, 53–77.
- Font, Josep Maria, 1997, “Belnap’s four-valued logic and De Morgan lattices”, Logic Journal of IGPL , 5: 1–29.
- –––, 2009, “Taking degrees of truth seriously”, Studia Logica , 91: 383–406.
- van Fraassen, Bas, 1966, “Singular terms, truth-value gaps, and free logic”, Journal of Philosophy , 63: 481–495.
- Frankowski, Szymon, 2004, “Formalization of a plausible inference”, Bulletin of the Section of Logic , 33: 41–52.
- Frege, Gottlob, 1884, Grundlagen der Arithmetik. Eine logisch-mathematische Untersuchung über den Begriff der Zahl , Hamburg: Felix Meiner Verlag, 1988.
- –––, 1891, “Function und Begriff. Vortrag, gehalten in der Sitzung vom 9. Januar 1891 der Jenaischen Gesellschaft für Medicin und Naturwissenschaft”, Jena: H. Pohle (Reprinted in Frege 1986.)
- –––, 1892, “Über Sinn und Bedeutung”, Zeitschrift für Philosophie und philosophische Kritik , 100: 25–50. (Reprinted in Frege 1986.)
- –––, 1893/1903, Grundgesetze der Arithmetik , 2 volumes, Jena: Verlag Hermann Pohle; reprinted, Darmstadt: Wissenschaftliche Buchgesellschaft, 1962.
- –––, 1918, “Der Gedanke”, Beiträge zur Philosophie des deutschen Idealismus 1: 58–77. (Reprinted in Frege 1967.)
- –––, 1967, Kleine Schriften , Ignacio Angelli (ed.), Darmstadt: Wissenschaftliche Buchgesellschaft.
- –––, 1976, Wissenschaftlicher Briefwechsel , G. Gabriel, H. Hermes, F. Kambartel, C. Thiel, and A. Veraart (eds.), Hamburg: Felix Meiner Verlag.
- –––, 1986, Funktion, Begriff, Bedeutung. Fünf logische Studien , G. Patzig (ed.), Göttingen: Vandenhoeck & Ruprecht.
- –––, 1990, “Einleitung in die Logik”, in Frege, G., Schriften zur Logik und Sprachphilosophie , Hamburg: Felix Meiner Verlag, 74–91.
- Gabriel, Gottfried, 1984, “Fregean connection: Bedeutung, value and truth-value”, The Philosophical Quarterly , 34: 372–376.
- –––, 1986, “Frege als Neukantianer”, Kant-Studien , 77: 84–101.
- –––, 2013, “Truth, value, and truth value. Frege’s theory of judgement and its historical background”, in M. Textor (ed.), Judgement and Truth in Early Analytic Philosophy and Phenomenology , Basingstoke: Palgrave Macmillan, 36–51.
- Galatos, Nikolaos, Peter Jipsen, Tomasz Kowalski and Hiroakira Ono, 2007, Residuated Lattices: An Algebraic Glimpse at Substructural Logics , Amsterdam: Elsevier.
- Geach, Peter and Max Black (eds.), 1952, Translations from the Philosophical Writings of Gottlob Frege , New York: Philosophical Library.
- Ginsberg, Matthew, 1988, “Multivalued logics: a uniform approach to reasoning in AI”, Computer Intelligence , 4: 256–316.
- Gödel, Kurt, 1944, “Russell’s mathematical logic”, in P.A. Schilpp (ed.), The Philosophy of Bertrand Russell , Evanston and Chicago: Northwestern University Press, 125–53.
- Goldblatt, Robert, 2006, Topoi: The Categorial Analysis of Logic , Mineola, NY: Dover Publications.
- Gottwald, Siegfried, 1989, Mehrwertige Logik. Eine Einführung in Theorie und Anwendungen , Berlin: Akademie-Verlag.
- –––, 2001, A Treatise on Many-valued Logic , Baldock: Research Studies Press.
- Goguen, Joseph, 1969, “The logic of inexact concepts”, Synthese , 19: 325–373.
- Grossmann, Reinhardt, 1992, The Existence of the World , London: Routledge.
- Haack, Susan, 1996, Deviant Logic, Fuzzy Logic. Beyond the Formalism , Chicago: University of Chicago Press.
- Hajek, Petr, 1998, Metamathematics of fuzzy logic , Dordrecht: Kluwer Academic Publishers.
- Jennings, Ray and Peter Schotch, 1984, “The preservation of coherence”, Studia Logica , 43: 89–106.
- Kamide, Norihiro and Heinrich Wansing, 2009, “Sequent calculi for some trilattice logics”, Review of Symbolic Logic , 2: 374–395.
- Kapsner, Andreas, 2019, “Removing the oddity in first degree entailment”, Thought. A Journal of Philosophy , 48: 240–249.
- Karpenko, Alexander, 1983, “Factor semantics for \(n\)-valued logics”, Studia Logica , 42: 179–185.
- Keefe, Rosanna, 2000, Theories of Vagueness , Cambridge: Cambridge University Press.
- Kneale, William and Martha Kneale, 1962, The Development of Logic , Oxford: Oxford University Press.
- Lewis, Clarence Irving, 1943, “The modes of meaning”, Philosophy and Phenomenological Research , 4: 236–249.
- Lewis, David, 1982, “Logic for equivocators”, Noûs, 16: 431–441.
- Lowe, Jonathan, 1995, “The metaphysics of abstract objects”, The Journal of Philosophy , 92: 509–524.
- –––, 1997, “Objects and criteria of identity”, in A Companion to the Philosophy of Language , R. Hale and C. Wright (eds.), Oxford: Basil Blackwell, 613–33.
- Łukasiewicz, Jan, 1918, “Farewell lecture by professor Jan Łukasiewicz,” delivered in the Warsaw University Lecture Hall in March, 1918, in Łukasiewicz 1970, 87–88.
- –––, 1920, “O logice trójwartościowej”, Ruch Filozoficny , 5: 170–171. (English translation as “On three-valued logic” in Łukasiewicz 1970, 87–88.)
- –––, 1921, “Logika dwuwartościowa”, Przegl ad Filosoficzny , 13: 189–205. (English translation as “Two-valued logic” in Łukasiewicz 1970, 89–109.)
- –––, 1970, Selected Works , L. Borkowski (ed.), Amsterdam: North-Holland, and Warsaw: PWN.
- MacFarlane, John, 2002, “Review of Stephen Neale, Facing Facts ”, Notre Dame Philosophical Reviews , [ MacFarlane 2002 available online ].
- –––, 2008, “Truth in the garden of forking paths”, in Relative Truth , Max Kölbel and Manuel García-Carpintero (eds.), Oxford: Oxford University Press, 81–102.
- Malinowski, Grzegorz, 1990, “Q-consequence operation”, Reports on Mathematical Logic , 24: 49–59.
- –––, 1993, Many-Valued Logics , Oxford: Clarendon Press.
- –––, 1994, “Inferential many-valuedness”, in Jan Wolenski (ed.), Philosophical Logic in Poland , Dordrecht: Kluwer Academic Publishers, 75–84.
- Mehlberg, Henryk, 1958, The Reach of Science , Toronto: University of Toronto Press.
- Meyer, Robert K., 1978 Why I Am Not a Relevantist , Research Paper No. 1, Canberra: Australian National University (Logic Group, Research School of the Social Sciences).
- Neale, Stephen, 1995, “The Philosophical significance of Gödel’s slingshot”, Mind , 104: 761–825.
- –––, 2001, Facing Facts , Oxford: Oxford University Press.
- Odintsov, Sergei, 2009, “On axiomatizing Shramko-Wansing’s logic”, Studia Logica , 93: 407–428. doi:10.1007/s11225-009-9181-6
- Odintsov, Sergei and Heinrich Wansing, 2015, “The logic of generalized truth values and the logic of bilattices”, Studia Logica , 103(1): 91–112. doi:10.1007/s11225-014-9546-3
- Oller, Carlos, 1999, “Paraconsistency and analyticity”, Logic and Logical Philosophy , 7: 91–99.
- Omori, Hitoshi and Daniel Skurt, (2019), “ SIXTEEN \(_3\) in light of Routley stars”, in R. Iemhoff, R. Moortgat, and R. de Queiroz R. (eds), Logic, Language, Information, and Computation . WoLLIC 2019 (Lecture Notes in Computer Science: Volume 11541), Berlin: Springer, 516–532.
- Omori, Hitoshi and Heinrich Wansing, 2017, “40 years of FDE: and introductory overview”, Studia Logica , 105: 1021–1049.
- Oppy, Graham, 1997, “The Philosophical Insignificance of Gödel’s Slingshot”, Mind , 106(421): 121–141.
- Peirce, C.S., 1885, “On the Algebra of Logic: A Contribution to the Philosophy of Notation”, American Journal of Mathematics , 7(2): 180–202. doi:10.2307/2369451
- Perry, John, 1996, “Evading the slingshot”, in A. Clark, J. Ezquerro, and J. Larrazabal (eds.), Philosophy and Cognitive Science. Categories, Consciousness, and Reasoning , Dordrecht: Kluwer Academic Publishers, 95–114.
- Pietroski, Paul M., 2018, Conjoining Meanings. Semantics Without Truth Values , Oxford: Oxford University Press.
- Predelli, Stefano, 2013, Meaning without Truth , Oxford: Oxford University Press.
- Popper, Karl, 1972, Objective Knowledge: An Evolutionary Approach , Oxford: Oxford University Press.
- Post, Emil, 1921, “Introduction to a general theory of elementary propositions”, American Journal of Mathematics , 43: 163–185.
- Priest, Graham, 1979, “Logic of Paradox”, Journal of Philosophical Logic , 8: 219–241.
- Quine, Willard Van Orman, 1953, “Reference and modality”, in W.v.O. Quine, From a Logical Point of View , Cambridge, MA: Harvard University Press, 139–159.
- –––, 1960, Word and Object , Cambridge, MA: MIT Press.
- –––, 1969, Ontological Relativity and Other Essays , New York: Columbia University Press.
- Reck, Erich, 2007, “Frege on truth, judgment, and objectivity”, Grazer Philosophische Studien , 75: 149–173.
- Rescher, Nicholas, 1969, Many-Valued Logic , New York: McGraw-Hill.
- Routley, Richard, 1975, “Universal semantics?”, The Journal of Philosophical Logic , 4: 327–356.
- Ruffino, Marco, 2003, “Wahrheit als Wert und als Gegenstand in der Logik Freges”, in D. Greimann (ed.), Das Wahre und das Falsche. Studien zu Freges Auffassung von Wahrheit , Hildesheim: Georg Olms Verlag, 203–221.
- Russell, Bertrand, 1918, 1919 [1992], “The philosophy of logical atomism”, Monist , 28: 495–527; 29: 32–63, 190–222, 345–380. reprinted in his Logic and Knowledge , London: Allen and Unwin, 1956. Page numbers from the Routlege edition, 1992, 175–282.
- Ryan, Mark and Martin Sadler, 1992, “Valuation systems and consequence relations”, in S. Abramsky, D. Gabbay, and T. Maibaum (eds.), Handbook of Logic in Computer Science , Vol. 1., Oxford: Oxford University Press, 1–78.
- Searle, John, 1995, “Truth: A Reconsideration of Strawson’s View”, in L.E. Hahn (ed.), The Philosophy of P.F. Strawson , Chicago: Open Court.
- Shramko, Yaroslav, 2014, “The logical way of being true: Truth values and the ontological foundation of logic”, Logic and Logical Philosophy .
- –––, 2016, “Truth, falsehood, information and beyond: the American Plan generalized”, in Katalin Bimbó (ed.), J. Michael Dunn on Information Based Logics (Outstanding Contributions to Logic: Volume 8), Berlin: Springer, 191–212.
- Shramko, Yaroslav, J. Michael Dunn, and Tatsutoshi Takenaka, 2001, “The trilaticce of constructive truth values”, Journal of Logic and Computation , 11: 761–788.
- Shramko, Yaroslav and Heinrich Wansing, 2005, “Some useful 16-valued logics: how a computer network should think”, Journal of Philosophical Logic , 34: 121–153.
- –––, 2006, “Hypercontradictions, generalized truth values, and logics of truth and falsehood”, Journal of Logic, Language and Information , 15: 403–424.
- –––, 2009a, “The Slingshot-Argument and sentential identity”, Studia Logica , 91: 429–455.
- –––, 2009b, “Editorial Introduction. Truth Values: Part I”, Studia Logica , 91: 295–304. doi:10.1007/s11225-009-9176-3
- –––, 2009c, “Editorial Introduction. Truth Values: Part II”, Studia Logica , 92: 143–146. doi:10.1007/s11225-009-9191-4
- –––, 2011, Truth and Falsehood: An Inquiry into Generalized Logical Values , Trends in Logic Vol. 36, Dordrecht, Heidelberg, London, New York: Springer.
- Sluga, Hans, 2002, “Frege on the indefinability of truth”, in E. Reck (ed.), From Frege to Wittgenstein: Perspectives on Early Analytic Philosophy , Oxford: Oxford University Press, 75–95.
- Stoutland, Frederick, 2003, “What philosophers should know about truth and the slingshot”, in Matti Sintonen, Petri Ylikoski, and Kaarlo Miller (eds.), Realism in Action: Essays in the Philosophy of the Social Sciences , Dordrecht: Kluwer Academic Publishers, 3–32. doi:10.1007/978-94-007-1046-7_1 (republished in: Fred Stoutland and Jeff Malpas, 2019, What Philosophers Should Know About Truth , Berlin, Boston: De Gruyter, pp. 1–34. doi:10.1515/9783110620788)
- Suszko, Roman, 1977, “The Fregean axiom and Polish mathematical logic in the 1920s”, Studia Logica , 36: 373–380. doi:10.1007/BF02120672
- Tarski, Alfred, 1930a, “Über einige fundamentale Begriffe der Metamathematik”, Comptes Rendus des Séances de la Société des Sciences et des Lettres de Varsovie XXIII, Classe III: 22–29.
- –––, 1930b, “Fundamentale Begriffe der Methodologie der deduktiven Wissenschaften, I”, Monatshefte für Mathematik und Physik , 37: 361–404.
- Taylor, Barry, 1985, Modes of Occurrence: Verbs, Adverbs and Events , Oxford: Blackwell.
- Truth Values. Part I, 2009, Special issue of Studia logica , Yaroslav Shramko and Heinrich Wansing (eds.), Vol. 91, No. 3.
- Truth Values. Part II, 2009, Special issue of Studia logica , Yaroslav Shramko and Heinrich Wansing (eds.), Vol. 92, No. 2.
- Urquhart, Alasdair, 1986, “Many-valued logic”, in D. Gabbay and F. Guenther (eds.), Handbook of Philosophical Logic , Vol. III., D. Reidel Publishing Co., Dordrecht, 71–116.
- Wansing, Heinrich, 2010, “The power of Belnap. Sequent systems for SIXTEEN \(_3\)”, Journal of Philosophical Logic , 39(4): 369–393. doi:10.1007/s10992-010-9139-1
- Wansing, Heinrich and Nuel Belnap, 2010, “Generalized truth values: A reply to Dubois”, Logic Journal of the IGPL , 18(6): 921–935. doi:10.1093/jigpal/jzp068
- Wansing, Heinrich and Yaroslav Shramko, 2008, “Suszko’s Thesis, inferential many-valuedness, and the notion of a logical system”, Studia Logica , 88: 405–429, 89: 147.
- Williamson, Timothy, 1994, Vagueness , London: Routledge.
- Windelband, Wilhelm, 1915, Präludien: Aufätze und Reden zur Philosophie und ihrer Geschichte , 5. Aufgabe, Bnd. 1., Tübingen.
- Wójcicki, Ryszard, 1970, “Some remarks on the consequence operation in sentential logics”, Fundamenta Mathematicae , 68: 269–279.
- –––, 1988, Theory of Logical Calculi. Basic Theory of Consequence Operations , Dordrecht: Kluwer Academic Publishers.
- Wrigley, Anthony, 2006, “Abstracting propositions”, Synthese , 151: 157–176.
- Zadeh, Lotfi, 1965, “Fuzzy sets”, Information and Control , 8: 338–53.
- –––, 1975, “Fuzzy logic and approximate reasoning”, Synthese , 30: 407–425.
- Zaitsev, Dmitry and Yaroslav Shramko, 2013, “Bi-facial truth: a case for generalized truth values”, Studia Logica , 101: 1299–1318.
- Zalta, Edward, 1983, Abstract Objects: An Introduction to Axiomatic Metaphysics , Dordrecht: D. Reidel Publishing Co.
How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.
[Please contact the authors with suggestions.]
abstract objects | Boolean algebra: the mathematics of | Frege, Gottlob | logic: classical | logic: fuzzy | logic: many-valued | Sorites paradox | truth: deflationism about | vagueness
Copyright © 2020 by Yaroslav Shramko < shramko @ rocketmail . com > Heinrich Wansing < Heinrich . Wansing @ rub . de >
- Accessibility
Support SEP
Mirror sites.
View this site from another server:
- Info about mirror sites
The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University
Library of Congress Catalog Data: ISSN 1095-5054
| Introduction to Logic |
| Satisfiability |
| The propositional satisfiability problem (often called SAT) is the problem of determining whether a set of sentences in Propositional Logic is satisfiable. The problem is significant both because the question of satisfiability is important in its own right and because many other questions in Propositional Logic can be reduced to that of propositional satisfiability. In practice, many automated reasoning problems in Propositional Logic are first reduced to satisfiability problems and then by using a satisfiability solver. Today, SAT solvers are commonly used in hardware design, software analysis, planning, mathematics, security analysis, and many other areas. In the chapter, we look at several basic methods for solving SAT problems. We begin with a review of the Truth Table Method. We then introduce the Backtracking Approach, and we show how it can be improved with Simplification and Unit Propagation. We briefly mention the popular DPLL method. Finally, we talk about non-guaranteed methods, with emphasis on one particular method, called GSAT. Let Δ = { ∨ , ∨¬ , ¬ ∨ , ¬ ∨¬ ∨¬ , ¬ ∨ }. We want to determine whether Δ is satisfiable. So, we build a truth table for this case. See below. | ∨ | ∨¬ | ¬ ∨ | ¬ ∨¬ ∨¬ | ¬ ∨ | Δ | ||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
There is one row for each possible truth assignment. For each truth assignment, each of the sentences in Δ is evaluated. If any sentence evaluates to 0, then Δ as a whole is not satisfied by the truth assignment. If a satisfying truth assignment is found, then Δ is determined to be satisfiable. If no satisfying truth assignment is found, then Δ is unsatisfiable. In this example, every row ends with Δ not satisfied. So the truth table method concludes that Δ is unsatisfiable.
The truth table method is complete because every truth assignment is checked. However, the method is impractical for all but very small problem instances. In our example with 3 propositions, there are 2 3 = 8 rows. For a problem instance with 10 propositions, there are 2 10 = 1024 rows - still quite small for a modern computer. But as the number of propositions grow, the number of rows quickly overwhelms even the fastest computers. A more efficient method is needed.
3. Backtracking
Looking at the example in the preceding section, we can observe that, often times, a partial truth assignment is all that is required to determine whether the input Δ is satisfied.
For example, let's consider the partial assignment { p = 1 , q = 0}. Even without the truth value for r , we can see that ¬ p ∨ q evaluates to 0 and therefore Δ is not satisfied. Furthermore, we can conclude that no truth assignment that extends this partial assignment can satisfy Δ because the sentence ¬ p ∨ q would always evaluate to 0 in every extension. So by determining whether the input in satisfied by a partial assignment, we can save the work of checking all extensions of the partial assignment. In this case, we can conclude that neither the truth assignment { p = 1, q = 0, r = 0} nor the assignment { p = 1, q = 0, r = 1} satisfies Δ. The saving is small in this case; but, as the number of propositions increases, there can be many more truth assignments we can eliminate from consideration. Backtracking allows us to realize this saving.
To search the space of truth assignments systematically, both partial and complete, we can set the propositions one at a time. The process can be visualized as a tree search where each branch sets the truth value of a single proposition, each interior node is a partial truth assignment, and each leaf node is a complete truth assignment. Below is a tree whose fringe represents all complete truth assignments.
In basic backtracking search, we start at the root of the tree (the empty assignment where nothing is known) and work our way down a branch. At each node, we check whether the input Δ is satisfied. If Δ is satisfied, we move down the branch by choosing a truth value for a currently unassigned proposition. If Δ is falsified, then, knowing that all the (partial) truth assignments further down the branch also falsify Δ, we backtrack to the most recent decision point and proceed down a different branch. At some point, we will either find a truth assignment that satisfies all the sentences of Δ or determine that none exists.
Let's look at an example. At each step, we show the part of the tree explored so far. An × mark at a node indicates that the truth assignment at that node falsifies at least one sentence in Δ. A ✓ indicates that the truth assignment at that node satisfies all the sentences in Δ. If neither is the case, the node is marked by a ? to indicate that the partial truth assignment at the node neither satisfies nor falsifies Δ.
Let's look at an example. At each step, we show the part of the tree explored so far. A boxed node is the current node. An × mark at a node indicates that the truth assignment at that node falsifies at least one sentence in Δ. A ✓ indicates that the truth assignment at that node satisfies all the sentences in Δ. A ? indicates that the partial truth assignment at the node neither satisfies nor falsifies Δ.
Let's start with the assumption that p is false. This leads to the partial tree shown below.
Now, let's assume that q is false. In this case, Δ is falsified, and the current branch is closed.
Since the current branch is closed, we backtrack to the most recent choice point where another branch can be taken. This time, let's assume that q is true.
Again, Δ is falsified, and the current branch is closed. Again we backtrack to the most recent choice point where another branch can be taken. Let p be true.
Let q be false.
Again, our sentences are falsified, and we backtrack. Let q be true.
Let r be false.
Our sentences are falsified by this assignment, and we backtrack one last time. Let r be true.
Once again, our sentences are falsified. Since all branches have been explored and closed, the method determines that Δ is unsatisfiable.
Looking at the full search tree compared to the portion explored by the basic backtracking search, we can see that the greyed out subtrees are all pruned from the search space. In this particular example, the savings are not spectacular. But in a bigger example with more propositions, the pruned subtrees can be much bigger.
4. Simplification and Unit Propagation
In this section, we consider two optimizations of basic backtracking search - simplification and unit propagation . In order for these methods to work, we assume that our sentences have been transformed into logically equivalent disjunctions (using a method like the one described in Chapter 5). As we choose the truth values of some propositions in a partial truth assignment for these disjunctions, there are opportunities to simplify the set of sentences that need to be checked.
Suppose, for example, a proposition p has been assigned the truth value 1. (1) Each disjunction containing a disjunct p may be ignored because it must already be satisfied by the current partial assignment. (2) Each disjunction φ containing a disjunct ¬ p may be modified (call the result φ') by removing from it all occurrences of the disjunct ¬ p because, under all truth assignments where p has truth value 1, φ holds if and only if φ' holds.
If a proposition p has been assigned the truth value 0, we can simplify our sentences analogously. (1) Each disjunction containing a disjunct ¬ p may be ignored because it must already be satisfied by the current partial assignment. (2) Each disjunction φ containing a disjunct p may be modified by removing from it all occurrences of the disjunct p .
Consider once again the example in the preceding section. Under the partial assignment p =1, we can simply our sentences as shown below. The first two sentences are dropped, and the literal ¬ p is dropped from the other three sentences.
| Original | Simplified | |
|---|---|---|
| ∨ | − | |
| ∨ ¬ | − | |
| ¬ ∨ | ||
| ¬ ∨ ¬ ∨ ¬ | ¬ ∨ ¬ | |
| ¬ ∨ | ||
While simplifying sentences is helpful in and of itself, the real value of simplification is that it enables a further optimization that can drastically decrease the search space.
In the course of the backtracking search, if we see a sentence that consists of single atom, say p , we know that the only possible satisfying assignments further down the branch must set p to true. In this case, we can fix p to be true and ignore the subbranch that sets p to false. Similarly, when we encounter a sentence that consists of a single negated atom, say ¬ p , we can fix p to be false and ignore the other subbranch. This optimization is called unit propagation because sentences of the form p or ¬ p are called units .
To start, let p be false.






COMMENTS
Understanding the concept of "truth assignment".
In this video we explain how to assign truth values to well-formed sentential formulas starting from a truth assignment for its sentential variables.
Truth Assignment. A truth assignment for a propositional vocabulary is a function assigning a truth value to each of the proposition constants of the vocabulary. In this book, we use the digit 1 as a synonym for true and 0 as a synonym for false; and we refer to the value of a constant or expression under a truth assignment i by superscripting ...
A truth assignment is a specific way of assigning truth values, either true or false, to the atomic propositions in a logical expression. It serves as a foundational concept in determining the overall truth value of more complex logical statements by evaluating how these atomic parts interact under different logical operators. Understanding truth assignments is crucial for analyzing logical ...
A truth assignment satisfies a sentence if and only if the sentences is true under that truth assignment according to rules defining the logical operators of the language. Evaluation is the process of determining the truth values of a complex sentence, given a truth assignment for the truth values of proposition constants in that sentence.
Mathematical logic. In mathematical logic (especially model theory), a valuation is an assignment of truth values to formal sentences that follows a truth schema. Valuations are also called truth assignments. In propositional logic, there are no quantifiers, and formulas are built from propositional variables using logical connectives.
A truth assignment is a specific mapping of truth values to the variables in propositional logic. This means that each variable in a logical expression is assigned either 'true' or 'false', which allows us to determine the overall truth value of complex expressions built from those variables. Truth assignments are crucial in understanding how different combinations of truth values affect the ...
A truth assignment for a Relational Logic language is a mapping that assigns a truth value to each element of it Herbrand base. The truth or falsity of compound sentences is determined from a truth assignment using rules based on the five logical operators of the language.
The formulas must be simultaneously satisfied by the same truth assignment. One way to determine consistency is as follows. Given a collection of propositions \(p_1,p_2,\ldots,p_n\), the propositions are consistent if their conjunction is satisfiable. That is, the following formula has at least one truth assignment that makes it true:
Formally, a truth assignment for a propositional vocabulary is a function assigning a truth value to each element of the Herbrand base. In what follows, we use the digit 1 as a synonym for true and 0 as a synonym for false ; and we refer to the value of a constant or expression under a truth assignment i by superscripting the constant or ...
9.4 Non-Boolean Models. A model in Relational Logic is an assignment of truth values to the ground atoms of our language. We treat each ground atom in our language as a variable and assign it a single truth value (1 or 0). In general, this is a good way to proceed.
A set of truth values: F (falsity), T (truth). A truth assignment for a set S of sentence symbols is a function v: S → {F, T} . We further consider the extension v¯¯¯:S¯¯¯ → {F, T} defined on the set S¯¯¯ of all wffs built up from S such that. a) for a sentence symbol A ∈ S , v¯¯¯(A) = v(A) , and. b) for wffs α, β ∈S¯¯¯ ,
Example 1.3.1. If p and q are propositional variables and V = { p, q } then there is a truth assignment v for V such that v ( p) = T and v ( q) = F. This is one of the four different truth assignments for a set of two propositional variables. In general, if you have n propositional variables then there are 2 n different truth ...
3.1 Introduction. Satisfaction is a relationship between specific sentences and specific truth assignments. In Logic, we are usually more interested in properties and relationships of sentences that hold across all truth assignments. We begin this chapter with a look at logical properties of individual sentences (as opposed to relationships ...
These assignment functions will formalize what it means to interpret a term or a formula in a structure. Definition 1.7.1. If \(\mathfrak{A}\) is an \(\mathcal{L}\)-structure, a variable assignment function into \(\mathfrak{A}\) is a function \(s\) that assigns to each variable an element of the universe \(A\). So a variable assignment function ...
A sentence is valid if and only if it is satisfied by every truth assignment. For example, the sentence (p ∨ ¬p) is valid. If a truth assignment makes p true, then the first disjunct is true and the disjunction as a whole true. If a truth assignment makes p false, then the second disjunct is true and the disjunction as a whole is true.
A truth table for a propositional language is a table showing all of the possible truth assignments for the proposition constants in the language. The columns of the table correspond to the proposition constants of the language, and the rows correspond to different truth assignments for those constants.
Lesson 3 - Propositional Analysis. 3.1 Introduction. Satisfaction is a relationship between specific sentences and specific truth assignments. In Logic, we are usually more interested in properties and relationships of sentences that hold across all truth assignments. We begin this chapter with a look at logical properties of individual ...
Truth Values - Stanford Encyclopedia of Philosophy
To search the space of truth assignments systematically, both partial and complete, we can set the propositions one at a time. The process can be visualized as a tree search where each branch sets the truth value of a single proposition, each interior node is a partial truth assignment, and each leaf node is a complete truth assignment. ...
Truth | Definition, Importance, Theories, & Facts
Alternatively, we can classify sentences into two overlapping categories. A sentence is satisfiable if and only if it is satisfied by at least one truth assignment, i.e. it is either valid or contingent. A sentence is falsifiable if and only if there is at least one truth assignment that makes it false, i.e. it is either contingent or ...
Lesson 3.5. Logical Consistency. a sentence ψ if and only if there is a truth assignment that satisfies both φ and ψ. A sentence ψ is a set of sentences Δ if and only if there is a truth assignment that satisfies both Δ and ψ. As with logical equivalence and logical entailment, we can use the truth table method to determine logical ...