Problems on Trigonometric Ratios
Some trigonometric solutions based problems on trigonometric ratios are shown here with the step-by-step explanation.
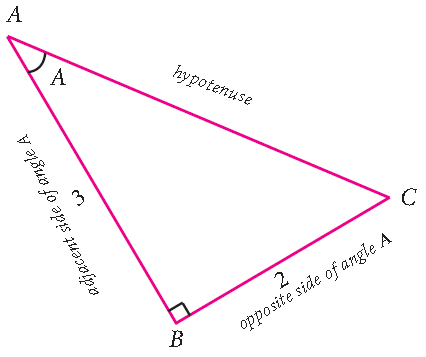
1. If sin θ = 8/17, find other trigonometric ratios of <θ.
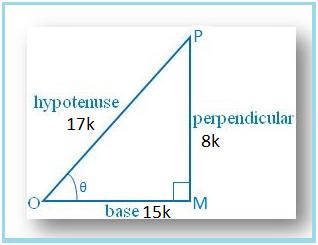
Let us draw a ∆ OMP in which ∠M = 90°.
Then sin θ = MP/OP = 8/17.
Let MP = 8k and OP = 17k, where k is positive.
By Pythagoras’ theorem, we get
Therefore, sin θ = MP/OP = 8k/17k = 8/17
cos θ = OM/OP = 15k/17k = 15/17
tan θ = Sin θ/Cos θ = (8/17 × 17/15) = 8/15
csc θ = 1/sin θ = 17/8
sec θ = 1/cos θ = 17/15 and
cot θ = 1/tan θ = 15/8.
2. If Cos A = 9/41, find other trigonometric ratios of ∠A.
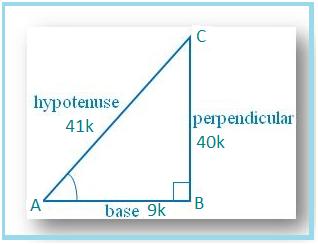
Let us draw a ∆ ABC in which ∠B = 90°.
Then cos θ = AB/AC = 9/41.
Let AB = 9k and AC = 41k, where k is positive.
Therefore, sin A = BC/AC = 40k/41k = 40/41
cos A = AB/AC = = 9k/41k = 9/41
tan A = Sin A/Cos A = (40/41 × 41/9) = 40/9
csc A = 1/sin A = 41/40
sec A = 1/cos A = 41/9 and
cot A = 1/tan A = 9/40.
3. Show that the value of sin θ and cos θ cannot be more than 1.
We know, in a right angle triangle the hypotenuse is the longest side.
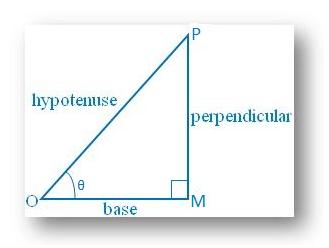
sin θ = perpendicular/hypotenuse = MP/OP < 1 since perpendicular cannot be greater than hypotenuse; sin θ cannot be more than 1.
Similarly, cos θ = base/hypotenuse = OM/OP < 1 since base cannot be greater than hypotenuse; cos θ cannot be more than 1.
4. Is that possible when A and B be acute angles, sin A = 0.3 and cos B = 0.7?
Since A and B are acute angles, 0 ≤ sin A ≤ 1 and 0 ≤ cos B ≤ 1, that means the value of sin A and cos B lies between 0 to 1. So, it is possible that sin A = 0.3 and cos B = 0.7
5. If 0° ≤ A ≤ 90° can sin A = 0.4 and cos A = 0.5 be possible?
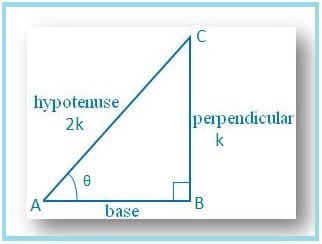
Let us draw a ∆ ABC in which ∠B = 90° and ∠BAC = θ.
Then sin θ = BC/AC = 1/2.
Let BC = k and AC = 2k, where k is positive.
= 3√3/2 - 4 × 3√3/8
= 3√3/2 - 3√3/2
Hence, (3cos θ - 4 cos<sup>3</sup> θ) = 0.
7. Show that sin α + cos α > 1 when 0 ° ≤ α ≤ 90°
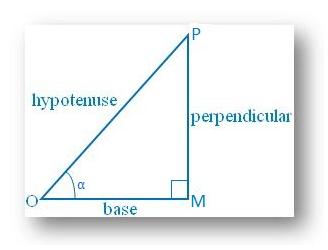
From the right triangle MOP,
Sin α = perpendicular/ hypotenuse
Cos α = base/ hypotenuse
Now, Sin α + Cos α
= perpendicular/ hypotenuse + base/ hypotenuse
= (perpendicular + base)/hypotenuse, which is > 1, Since we know that the sum of two sides of a triangle is always greater than the third side.
8. If cos θ = 3/5, find the value of (5csc θ - 4 tan θ)/(sec θ + cot θ)
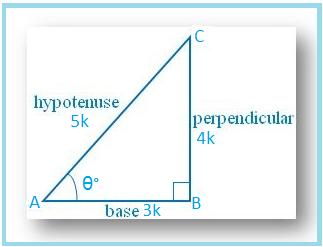
Let ∠A = θ°
Then cos θ = AB/AC = 3/5.
Let AB = 3k and AC = 5k, where k is positive.
Therefore, sec θ = 1/cos θ = 5/3
tan θ = BC/AB =4k/3k = 4/3
cot θ = 1/tan θ = 3/4 and
csc θ = AC/BC = 5k/4k = 5/4
Now (5csc θ -4 tan θ)/(sec θ + cot θ)
= (5 × 5/4 - 4 × 4/3)/(5/3 + 3/4)
= (25/4 -16/3)/(5/3 +3/4)
= 11/12 × 12/29
9. Express 1 + 2 sin A cos A as a perfect square.
1 + 2 sin A cos A
10. If sin A + cos A = 7/5 and sin A cos A =12/25, find the values of sin A and cos A.
sin A + cos A = 7/5
⇒ cos A = 7/5 - sin θ
Now from sin θ/cos θ = 12/25
We get, sin θ(7/5 - sin θ) = 12/25
or, 5 sin θ(5 sin θ - 4) - 3(5 sin θ - 4) = 0
or, (5 sin θ - 3) (5 sin θ - 4) = 0
⇒ (5 sin θ - 3) = 0 or, (5 sin θ - 4) = 0
⇒ sin θ = 3/5 or, sin θ = 4/5
When sin θ = 3/5, cos θ = 12/25 × 5/3 = 4/5
Again, when sin θ = 4/5, cos θ = 12/25 × 5/4 = 3/5
Therefore, sin θ =3/5, cos θ = 4/5
or, sin θ =4/5, cos θ = 3/5.
11. If 3 tan θ = 4, evaluate (3sin θ + 2 cos θ)/(3sin θ - 2cos θ).
Solution: Given,
3 tan θ = 4
⇒ tan θ = 4/3
(3sin θ + 2 cos θ)/(3sin θ - 2cos θ)
= (3 tan θ + 2)/(3 tan θ - 2), [dividing both numerator and denominator by cos θ]
= (3 × 4/3 + 2)/(3 × 4/3 -2), putting the value of tan θ = 4/3
12. If (sec θ + tan θ)/(sec θ - tan θ) = 209/79, find the value of θ.
Solution: (sec θ + tan θ)/(sec θ - tan θ) = 209/79
⇒ [(sec θ + tan θ) - (sec θ - tan θ)]/[(sec θ + tan θ) + (sec θ - tan θ)] = [209 – 79]/[209 + 79], (Applying componendo and dividendo)
⇒ 2 tan θ/2 sec θ =130/288
⇒ sin θ/cos θ × cos θ = 65/144
⇒ sin θ = 65/144.
13. If 5 cot θ = 3, find the value of (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ).
Given 5 cot θ = 3
⇒ cot θ = 3/5
Now (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ)
= (5 - 3 cot θ)/(4 sin θ + 3 cot θ), [dividing both numerator and denominator by sin θ]
= (5 - 3 × 3/5)/(4 + 3 × 3/5)
= (5 - 9/5)/(4 + 9/5)
= (16/5 × 5/29)
⇒ sin θ(sin θ - 2) - 1(sin θ - 2) = 0
⇒ (sin θ - 2)(sin θ - 1) = 0
⇒ (sin θ - 2) = 0 or, (sin θ - 1) = 0
⇒ sin θ = 2 or, sin θ = 1
So, value of sin θ can’t be greater than 1,
Therefore sin θ = 1
Basic Trigonometric Ratios
Relations Between the Trigonometric Ratios
Reciprocal Relations of Trigonometric Ratios
Trigonometrical Identity
Problems on Trigonometric Identities
Elimination of Trigonometric Ratios
Eliminate Theta between the equations
Problems on Eliminate Theta
Trig Ratio Problems
Proving Trigonometric Ratios
Trig Ratios Proving Problems
Verify Trigonometric Identities
- 10th Grade Math
From Problems on Trigonometric Ratios to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Worksheet on data handling | questions on handling data |grouping data.
Aug 29, 24 10:10 AM
Construction of Bar Graphs | Examples on Construction of Column Graph
Aug 29, 24 02:26 AM
5th Grade Bar Graph | Definition | Interpret Bar Graphs|Free Worksheet
Aug 29, 24 02:11 AM
Worksheet on Pictographs | Picture Graph Worksheets | Pictograph Works
Aug 29, 24 12:38 AM

Pictographs | Pictorial Representation | Pictorial Symbols | Symbols
Aug 27, 24 05:56 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Trigonometry Practice Questions
Click here for questions, click here for answers.
Answers – Version 1
Answers – Version 2
GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
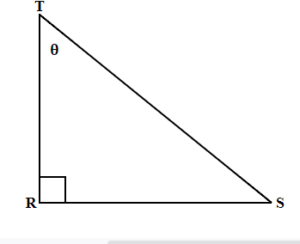
Solve Problems Using Trigonometric Ratios
| | A set of problems, that may be solved using the trigonometric ratios, is presented. Detailed solutions and explanations are included.
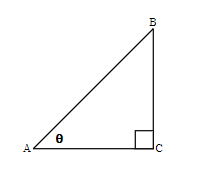
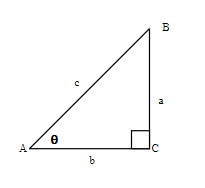
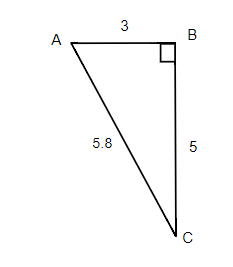
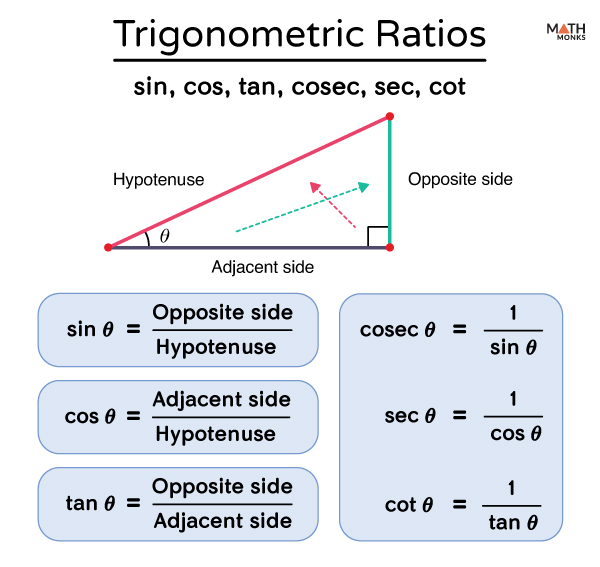
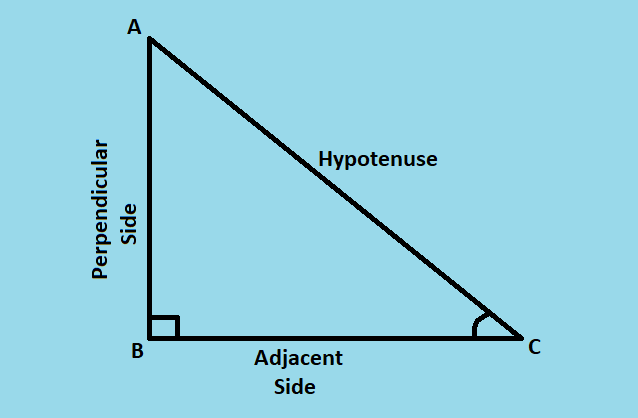
In a right triangle, the six trigonometric ratios; the ratio, the ratio, the ratio, the ratio, the ratio and the ratio are defined as follows: The sine of angle A = sin (A) = side opposite angle A / hypotenuse = a / c The cosine of angle A = cos (A) = side adjacent to angle A / hypotenuse = b / c The tangent of angle A = tan (A) = side opposite angle A / side adjacent to angle A = a / b The secant of angle A = sec (A) = hypotenuse / side adjacent to angle A = c / b The cosecant of angle A = csc (A) = hypotenuse / side opposite to angle A = c / a The cotangent of angle A = cot (A) = side adjacent to angle A / side opposite angle A = b / a
(hypotenuse) = 8 + 6 = 100 and hypotenuse = 10 sin A = side opposite angle A / hypotenuse = 8 / 10 = 4 / 5 cos (A) = side adjacent to angle A / hypotenuse = 6 / 10 = 3 / 5 tan (A) = side opposite angle A / side adjacent to angle A = 8 / 6 = 4 / 3 sec (A) = hypotenuse / side adjacent to angle A = 10 / 6 = 5 / 3 csc (A) = hypotenuse / side opposite to angle A = 10 / 8 = 5 / 4 cot (A) = side adjacent to angle A / side opposite angle A = 6 / 8 = 3 / 4 sin A = opposite / hypotenuse sin 31 = 5.12 / c c = 5.12 / sin 31 c (approximately) = 9.94 sin 30 = x / 10 = 1 / 2 ( see ) to find x x = 5 10 = 5 + y y = √(75) = 5 √ (3) . |

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
CHAPTER 9 Trigonometry
9.2 Solve Applications: Sine, Cosine and Tangent Ratios.
Learning Objectives
By the end of this section, you will be able to:
- Find missing side of a right triangle using sine, cosine, or tangent ratios
- Find missing angle of a right triangle using sine, cosine, or tangent ratios
- Solve applications using right angle trigonometry
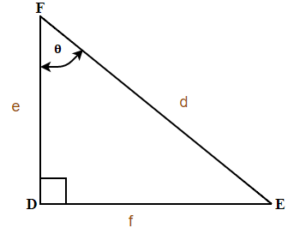
Sine, Cosine, and Tangent Ratios
We know that any right triangle has three sides and a right angle. The side opposite to the right angle is called the hypotenuse. The other two angles in a right triangle are acute angles (with a measure less than 90 degrees). One of those angles we call reference angle and we use θ (theta) to represent it.
The hypotenuse is always the longest side of a right triangle. The other two sides are called opposite side and adjacent side. The names of those sides depends on which of the two acute angles is being used as a reference angle.
In the right triangle each side is labeled with a lowercase letter to match the uppercase letter of the opposite vertex.
Label the sides of the triangle and find the hypotenuse, opposite, and adjacent.
We labeled the sides with a lowercase letter to match the uppercase letter of the opposite vertex.
c is hypotenuse
a is opposite
b is adjacent
Label the sides of the triangle and find the hypotenuse, opposite and adjacent.
y is hypotenuse
z is opposite
x is adjacent
r is hypotenuse
t is opposite
s is adjacent
Trigonometric Ratios
Trigonometric ratios are the ratios of the sides in the right triangle. For any right triangle we can define three basic trigonometric ratios: sine, cosine, and tangent.
Let us refer to Figure 1 and define the three basic trigonometric ratios as:
Three Basic Trigonometric Ratios
Where θ is the measure of a reference angle measured in degrees.
Very often we use the abbreviations for sine, cosine, and tangent ratios.
Some people remember the definition of the trigonometric ratios as SOH CAH TOA.
For the given triangle find the sine, cosine and tangent ratio.
For the given triangle find the sine cosine and tangent ratio.
When calculating we will usually round the ratios to four decimal places and at the end our final answer to one decimal place unless stated otherwise.
For the given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.
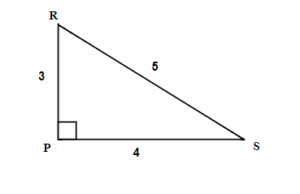
We have two possible reference angles: R an S.
Using the definitions, the trigonometric ratios for angle R are:
Using the definitions, the trigonometric ratios for angle S:
For the given triangle find the sine, cosine, and tangent ratios. If necessary round to four decimal places.
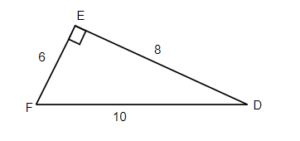
For given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.
Now, let us use a scientific calculator to find the trigonometric ratios. Can you find the sin, cos, and tan buttons on your calculator? To find the trigonometric ratios make sure your calculator is in Degree Mode.
Using a calculator find the trigonometric ratios. If necessary, round to 4 decimal places.
Make sure your calculator is in Degree Mode.
a) Using a calculator find that sin 30° = 0.5
b) Using a calculator find that cos 45° = 0.7071 Rounded to 4 decimal places.
c) Using a calculator find that tan 60° = 1.7321 Rounded to 4 decimal places.
Find the trigonometric ratios. If necessary, round to 4 decimal places.
a) sin 60°
b) cos 30°
c) tan 45°
a) sin 60° = 0.8660
b) cos 30° = 0.8660
c) tan 45° = 1
a) sin 35°
b) cos 67°
c) tan 83°
a) sin 35° = 0.5736
b) cos 67 ° = 0.3907
c) tan 83° = 8.1443
Finding Missing Sides of a Right Triangle
In this section you will be using trigonometric ratios to solve right triangle problems. We will adapt our problem solving strategy for trigonometry applications. In addition, since those problems will involve the right triangle, it is helpful to draw it (if the drawing is not given) and label it with the given information.We will include this in the first step of the problem solving strategy for trigonometry applications.
HOW TO: Solve Trigonometry Applications
- Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
- Identify what we are looking for.
- Label what we are looking for by choosing a variable to represent it.
- Find the required trigonometric ratio.
- Solve the ratio using good algebra techniques.
- Check the answer by substituting it back into the ratio in step 4 and by making sure it makes sense in the context of the problem.
- Answer the question with a complete sentence.
In the next few examples, having given the measure of one acute angle and the length of one side of the right triangle, we will solve the right triangle for the missing sides.
Find the missing sides. Round your final answer to two decimal places
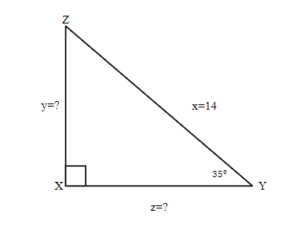
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle Y is our reference angle, y is opposite side, z is adjacent side, and x=14 is the hypotenuse. | |
| 2. what we are looking for. | a) the opposite side | b) adjacent side |
| 3. what we are looking for by choosing a variable to represent it. | y=? | z=? |
| 4. the required trigonometric ratio. | sin 35° = | cos 35° = |
| 5. the ratio using good algebra techniques. | 14 sin 35° = y 8.03 = y | 14 cos 35° = z 11.47 = z |
| 6. the answer in the problem and by making sure it makes sense. | 0.57 0.57 = 0.57 | 0.82 0.82 = 0.82 |
| 7. the question with a complete sentence. | The opposite side is 8.03 | The adjacent side is 11.47 |
Find the missing sides. Round your final answer to one decimal place.
Find the missing sides. Round your final answer to one decimal place.
Find the hypotenuse. Round your final answer to one decimal place.
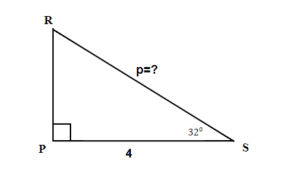
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle S is our reference angle, s is opposite side, r = 4 is the adjacent side, and p is the hypotenuse |
| 2. what we are looking for. | the hypotenuse |
| 3. what we are looking for by choosing a variable to represent it. | p=? |
| 4. the required trigonometric ratio. | cos 32° = |
| 5. the ratio using good algebra techniques. | 0.8480 = p = 4.7170 Rounding the ratios to 4 decimal places |
| 6. the answer in the problem and by making sure it makes sense. | 0.8480 0.8480 = 0.8480 |
| 7. the question with a complete sentence. | The hypotenuse is 4.7 Round my final answer to one decimal place. |
TRY IT 6.1..
Finding Missing Angles of a Right Triangle
Sometimes we have a right triangle with only the sides given. How can we find the missing angles? To find the missing angles, we use the inverse of the trigonometric ratios. The inverse buttons sin -1 , cos -1 , and tan -1 are on your scientific calculator.
Find the angles. Round your final answer to one decimal place.
a) sin A = 0.5
b) cos B = 0.9735
c) tan C = 2.89358
Use your calculator and press the 2nd FUNCTION key and then press the SIN, COS, or TAN key
a) A = sin -1 0.5
b) B = cos -1 0.9735
c) C = tan -1 2.89358
a) sin X = 1
b) cos Y = 0.375
c) tan Z = 1.676767
a) sin C = 0
b) cos D = 0.95
c) tan F = 6.3333
In the example below we have a right triangle with two sides given. Our acute angles are missing. Let us see what the steps are to find the missing angles.
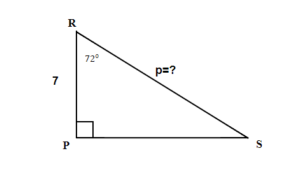
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle T is our reference angle, t = 7 is the opposite side, s is adjacent side, and r =11 is the hypotenuse |
| 2. what we are looking for. | angle T |
| 3. what we are looking for by choosing a variable to represent it. | |
| 4. the required trigonometric ratio. | sin T = |
| 5. the ratio using good algebra techniques. | sin T = 0.6364 T = sin 0.6364
|
| 6. the answer in the problem and by making sure it makes sense. | sin 39.5239° 0.6364 = 0.6364 |
| 7. the question with a complete sentence. | The missing angle T is 39.5°. |
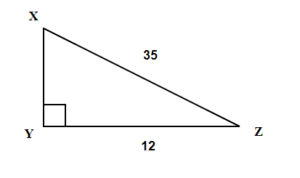
Find the missing angle X. Round your final answer to one decimal place.
Find the missing angle Z. Round your final answer to one decimal place.

Find the missing angle A. Round your final answer to one decimal place.
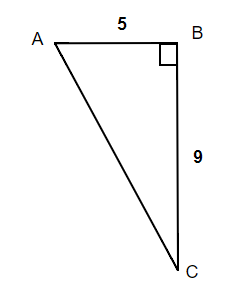
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle A is our reference angle, a = 9 is the opposite side, c = 5 is the adjacent side, and b is the hypotenuse |
| 2. what we are looking for. | angle A |
| 3. what we are looking for by choosing a variable to represent it. | |
| 4. the required trigonometric ratio. | tan A = |
| 5. the ratio using good algebra techniques. | tan A = 1.8 A = tan 1.8
|
| 6. the answer in the problem and by making sure it makes sense. | tan 60.9° 1.8 = 1.8 |
| 7. the question with a complete sentence. | The missing angle A is 60.9°. |
Find the missing angle C. Round your final answer to one decimal place.

Find the missing angle E. Round your final answer to one decimal place.
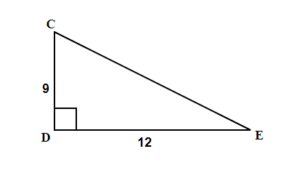
Solving a Right Triangle
From the section before we know that any triangle has three sides and three interior angles. In a right triangle, when all six parts of the triangle are known, we say that the right triangle is solved.
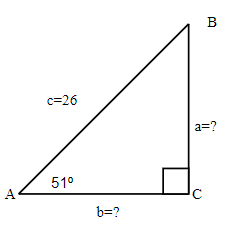
Solve the right triangle. Round your final answer to one decimal place.
Since the sum of angles in any triangle is 180°, the measure of angle B can be easy calculated.
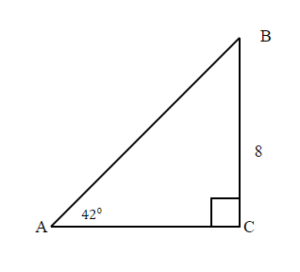
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle A is our reference angle, a = 8 is the opposite side, b is the adjacent side, and c is the hypotenuse. | |
| 2. what we are looking for. | a) adjacent side | b) hypotenuse |
| 3. what we are looking for by choosing a variable to represent it. | b = ? | c = ? |
| 4. the required trigonometric ratio. | tan 42° = | sin 42° = |
| 5. the ratio using good algebra techniques. | 0.9004 = 0.9004 b = 8 b = 8.8849 | 0.6691 = 0.6691 c = 8 c = 11.9563 |
| 6. the answer in the problem and by making sure it makes sense. | tan 42 ° 0.9 = 0.9 | sin 42° 0.6691 = 0.6691 |
| 7. the question with a complete sentence. | The adjacent side is 8.9. Rounded to one decimal place. | The hypotenuse is 12 |
We solved the right triangle
TRY IT 10.1
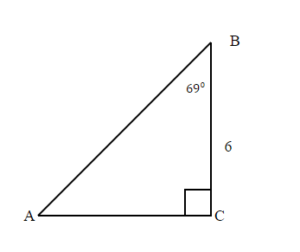
TRY IT 10.2
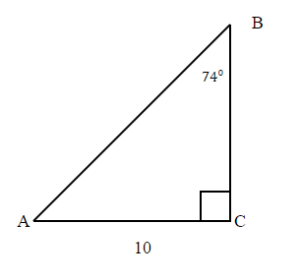
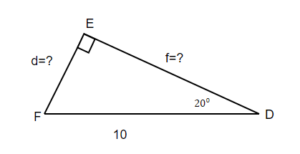
Solve the right triangle. Round to two decimal places.
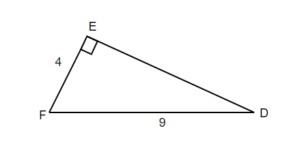
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Let angle D be our reference angle, d = 4 is the opposite side, f is the adjacent side, and e = 9 is the hypotenuse | |
| 2. what we are looking for. | a) angle D | b) adjacent |
| 3. what we are looking for by choosing a variable to represent it. | f = ? | |
| 4. the required trigonometric ratio. | sin D = | 4 + f = 9 |
| 5. the ratio using good algebra techniques. | sin D = 0.4444 D = sin 0.4444
| 16 + f = 81 f = 81 – 16 f = 65 f = square root of 65 f = 8.06 |
| 6. the answer in the problem and by making sure it makes sense. | sin 26.3850° 0.4444 =0.4444 | 4 + 8.06 81 = 81 |
| 7. the question with a complete sentence. | The missing angle D is 26.39°. | The adjacent side is 8.06 Rounded to two decimal places |
The missing angle F = 180° – 90° – 26.39° = 63.64°
TRY IT 11.1
Solve the right triangle. Round to one decimal place.
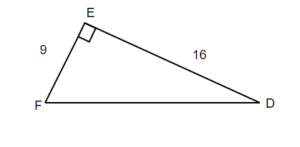
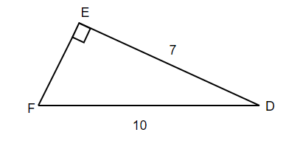
TRY IT 11.2
Solve Applications Using Trigonometric Ratios
In the previous examples we were able to find missing sides and missing angles of a right triangle. Now, let’s use the trigonometric ratios to solve real-life problems.
Many applications of trigonometric ratios involve understanding of an angle of elevation or angle of depression.
The angle of elevation is an angle between the horizontal line (ground) and the observer’s line of sight.
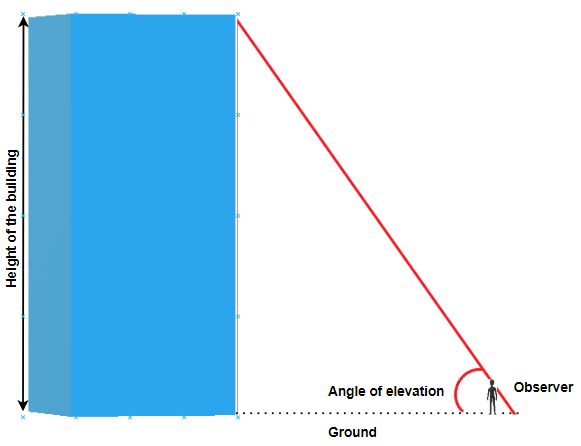
The angle of depression is the angle between horizontal line (that is parallel to the ground) and the observer’s line of sight.
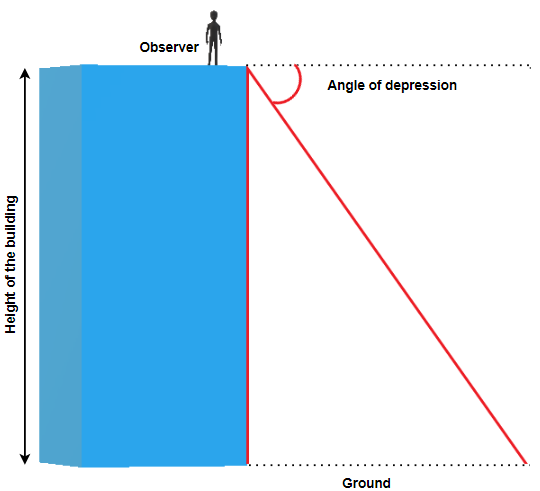
James is standing 31 metres away from the base of the Harbour Centre in Vancouver. He looks up to the top of the building at a 78° angle. How tall is the Harbour Centre?
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | Angle X is our reference angle, x is opposite side, y = 31 m is the adjacent side, and z is the hypotenuse. |
| 2. what we are looking for. | The opposite side |
| 3. what we are looking for by choosing a variable to represent it. | x=? |
| 4. the required trigonometric ratio. | tan 78° = |
| 5. the ratio using good algebra techniques. | 4.7046 = x = 145.8426 |
| 6. the answer in the problem and by making sure it makes sense. | 4.7046 4.7046 = 4.7046 |
| 7. the question with a complete sentence. | The Harbour Centre is 145.8426 metres or rounded to 146 metres. |
TRY IT 12.1
Nicole is standing 75 feet away from the base of the Living Shangri-La, the tallest building in British Columbia. She looks up to the top of the building at a 83.5° angle. How tall is the Living Shangri-La?
658.3 feet.
TRY IT 12.2
Kelly is standing 23 metres away from the base of the tallest apartment building in Prince George and looks at the top of the building at a 62° angle. How tall is the building?
43.3 metres
Thomas is standing at the top of the building that is 45 metres high and looks at his friend that is standing on the ground, 22 metres from the base of the building. What is the angle of depression?
| 1. the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. |
Angle Y is our reference angle, y = 45 m is the opposite side, z = 22 m is the adjacent side, and x is the hypotenuse |
| 2. what we are looking for. | angle Y |
| 3. what we are looking for by choosing a variable to represent it. | |
| 4. the required trigonometric ratio. | tan Y = |
| 5. the ratio using good algebra techniques. | tan Y = 2.0455 Y = tan ¹2.0455
|
| 6. the answer in the problem and by making sure it makes sense. | tan 63.9470° 2.0455 = 2.0455 |
| 7. the question with a complete sentence. | The angle of depression is 63.9470° or 64° rounded to one decimal place. |
TRY IT 13.1
Hemanth is standing on the top of a cliff 250 feet above the ground and looks at his friend that is standing on the ground, 40 feet from the base of the cliff. What is the angle of depression?
TRY IT 13.2
Klaudia is standing on the ground, 25 metres from the base of the cliff and looks up at her friend on the top of a cliff 100 metres above the ground. What is the angle of elevation?
Key Concepts
- Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
- Check the answer by substituting it back into the ratio solved in step 5 and by making sure it makes sense in the context of the problem.
Practice Makes Perfect
Label the sides of the triangle.
| 1
| 2.
|
| 3. If the reference angle in Question 1 is B, Find the adjacent ?
| 4. If the reference angle in Question 2 is Z, find the opposite ? |
| 5. | 6. |
Use your calculator to find the given ratios. Round to four decimal places if necessary:
| 7. | 8. |
| 9. | 10. |
For the given triangles, find the sine, cosine and tangent of the θ.
| 11. | 12. |
| 13. | 14. |
For the given triangles, find the missing side. Round it to one decimal place.
| 15. Find the hypotenuse. | 16. Find b if a = 6. |
| 17. Find the opposite. | 18. Find the adjacent. |
For the given triangles, find the missing sides. Round it to one decimal place.
| 19. | 20. |
Solve the triangles. Round to one decimal place.
| 21. | 22. |
| 23. | 24. |
| 25. A surveyor stands 75 metres from the bottom of a tree and looks up at the top of the tree at a 48° angle. How tall is the tree? | 26. A tree makes a shadow that is 6 metres long when the angle of elevation to the sun is 52°. How tall is the tree? |
| 27. A ladder that is 15 feet is leaning against a house and makes a 45° angle with the ground. How far is the base of the ladder from the house? | 28. Matt is flying a kite and has let out 100 feet of string. The angle of elevation with the ground is 38°. How high is his kite above the ground? |
| 29. Marta is flying a kite and has let out 28 metres of string. If the kite is 10 metres above the ground, what is the angle of elevation? | 30. An airplane takes off from the ground at the angle of 25°. If the airplane traveled 200 kilometres, how high above the ground is it? |
| 1.
| 3. c | 5.
g is opposite , f is adjacent, and e is hypotenuse |
| 7. 0.7314 | 9. 0.2126 | 11.
sin θ = |
| 13. sin θ = | 15. b = 19.8 | 17. c = 12 |
| 19. y = 19.3, z = 8.2 | 21.
b = 38.5 c = 21.3 d = 44 | 23.
t = 15 r = 25 s = 20 |
| 25. 83.3 m | 27. 10.6 ft | 29. 20.9° |
Introductory Algebra Copyright © 2021 by Izabela Mazur is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Table of Contents
Last modified on August 3rd, 2023
#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline
Trigonometric ratios.
Trigonometric ratios are the ratios of the side lengths of a right-angled triangle. Three common trigonometric ratios are the sine (sin), cosine (cos), and tangent (tan). There are three more trigonometric ratios, cosecant (cosec), secant (sec), and cotangent (cot), that is, the inverse of sine, cosine, and tangent.
Thus, it is used to determine the ratios of any 2 sides of a right-angled triangle with respect to specific angles.
The value of these trigonometric ratios is calculated using the measure of any special acute angle θ in a right-angled triangle.
The standard formulas for the given trigonometric ratios for θ (where θ is an acute angle) are:
Sine (sin) : It is the ratio of the opposite side (perpendicular side) to θ to the hypotenuse
∴ sin θ = Opposite side/ Hypotenuse
Cosine (cos) : It is the ratio of the adjacent side to θ to the hypotenuse
∴ cos θ = Adjacent side/ Hypotenuse
Tangent (tan) : It is the ratio of the opposite side to θ to the side adjacent to θ
∴ tan θ = Opposite side/ Adjacent side
Cosecant (cosec) : It is the multiplicative inverse of sine
∴ cosec θ = 1/sin θ = Hypotenuse /Opposite side
Secant (sec) : It is the multiplicative inverse of cosine
∴ sec θ = 1/cos θ = Hypotenuse/ Adjacent side
Cotangent (cot) : It is the multiplicative inverse of tangent
∴ cot θ = 1/tan θ = Adjacent side/Opposite side
In the given right-triangle ABC, the trigonometric ratios are shown:
Thus, with respect to ∠C, the ratios of trigonometry are:
- sine C = Side opposite to ∠C/Hypotenuse = AB/AC
- cos C = Side adjacent to ∠C/Hypotenuse = BC/AC
- tan C = Side opposite to ∠C/Side adjacent to ∠) = AB/BC = sin ∠C/cos ∠C
- cosec C= 1/sin C = Hypotenuse/ Side Opposite to ∠C = AC/AB
- sec C = 1/cos C = Hypotenuse/ Side Opposite to ∠C = AC/BC
- cot C = 1/tan C = Side adjacent to ∠C/Side opposite to ∠C = BC/AB
All the ratios written above for ∠C in all possible right triangles will be the same. The same being with ∠A
An Easy Way to Remember Trigonometric Ratios
The word sohcahtoa can be used to remember the trigonometric ratio formulas of sine, cosine, and tangent:
| SOH | ine is pposite over ypotenuse | Sin θ = Opposite side/ Hypotenuse |
| CAH | osine is djacent over Hypotenuse | Cos θ = Adjacent side/ Hypotenuse |
| TOA | angent is pposite over djacent | Tan θ = Opposite side/ Adjacent side |
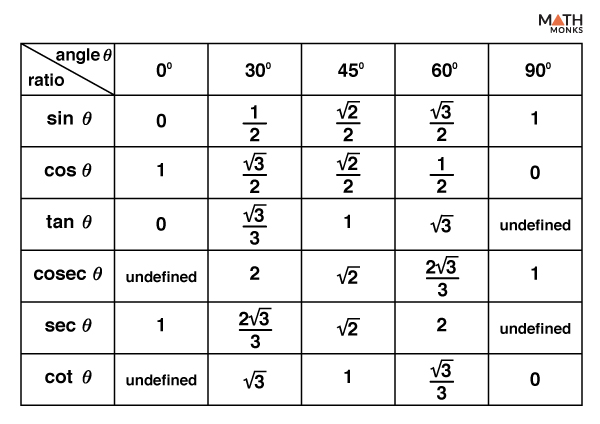
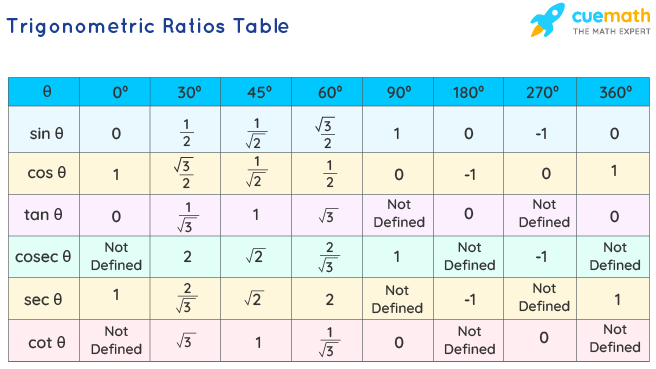
Trigonometric Ratios Table
The trigonometric ratios table displays the values of trigonometric ratios for the standard angles 0°, 30°, 45°, 60°, and 90° used in several trigonometric calculations.
Trigonometric Ratios Identities
Several trigonometric ratios identities make our calculations simpler such as:
- sin 2 θ + cos 2 θ = 1
- 1 + tan 2 θ = sec 2 θ
- 1 + cot 2 θ = cosec 2 θ
There are also some variations of the above 3 identities, which are nothing but rearranging the ones given above.
Trigonometric Ratios of Complementary Angles Identities
The complement of an angle θ is (90° – θ). Accordingly, the trigonometric ratios of complementary angles are:
- sin (90°- θ) = cos θ
- cos (90°- θ) = sin θ
- cosec (90°- θ) = sec θ
- sec (90°- θ) = cosec θ
- tan (90°- θ) = cot θ
- cot (90°- θ) = tan θ
Other Trigonometric Ratios Identities
The sum, difference, and product trigonometric ratios identities are:
- sin (A + B) = sin A cos B + cos A sin B
- sin (A – B) = sin A cos B – cos A sin B
- cos (A + B) = cos A cos B – sin A sin B
- cos (A – B) = cos A cos B + sin A sin B
- tan (A + B) = (tan A + tan B)/ (1 – tan A tan B)
- tan (A – B) = (tan A – tan B)/ (1 + tan A tan B)
- cot (A + B) = (cot A cot B – 1)/(cot B – cot A)
- cot (A – B) = (cot A cot B + 1)/(cot B – cot A)
- 2 sin A⋅cos B = sin(A + B) + sin(A – B)
- 2 cos A⋅cos B = cos(A + B) + cos(A – B)
- 2 sin A⋅sin B = cos(A – B) – cos(A + B)
The half, double, and triple-angles trigonometric ratios identities
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos 2 θ – sin 2 θ = = 2 cos 2 θ – 1 = 1 – 2 sin 2 θ = (1 – tan 2 θ)/(1 + tan 2 θ)
- sec 2θ = sec 2 θ/(2-sec 2 θ)
- cosec 2θ = (sec θ. cosec θ)/2
- cot 2θ = (cot θ – tan θ)/2
- sin 3θ = 3sin θ – 4sin 3 θ
- cos 3θ = 4cos 3 θ – 3cos θ
- tan 3θ = (3tanθ – tan 3 θ)/(1 – 3tan 2 θ)
Find the value of tan θ if sin θ = 14/5 and cos θ =6/9
As we know, tan θ = sin θ/cos θ, here sin θ = 14/5 and cos θ = 6/9 = (14/5)(6/9) = 63/15
2 thoughts on “ Trigonometric Ratios ”
what you provided me with was helpful
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&
- Inspiration
Trigonometric Ratios
Trigonometric ratios are the ratios of the length of sides of a triangle. These ratios in trigonometry relate the ratio of sides of a right triangle to the respective angle. The basic trigonometric ratios are sin, cos, and tan, namely sine, cosine, and tangent ratios. The other important trig ratios, cosec, sec, and cot, can be derived using the sin, cos, and tan respectively.
The word "Trigonometry" originated from the words, "Trigonon" which means "triangle" and "Metron" which means "to measure". It is a branch of mathematics that deals with the relation between the angles and sides of a right-angled triangle. In fact, trigonometry is one of the most ancient subjects which is studied by scholars all over the world. Let us understand the trigonometric ratios in detail in the following sections.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What are Trigonometric Ratios?
In trigonometry, there are six trigonometric ratios, namely, sine , cosine , tangent , secant, cosecant, and cotangent. These ratios are written as sin, cos, tan, sec, cosec(or csc), and cot in short. Let us have a look at the right-angled triangle shown below. Trigonometric ratios can be used to determine the ratios of any two sides out of a total of three sides of a right-angled triangle in terms of the respective angles.
The values of these trigonometric ratios can be calculated using the measure of an acute angle , θ in the right-angled triangle given below. This implies that the value of the ratio of any two sides of the triangle here depends on angle C. We can alternatively find the values of these trig ratios for angle A. Also, only the base and perpendicular will interchange for the given right triangle in that case.
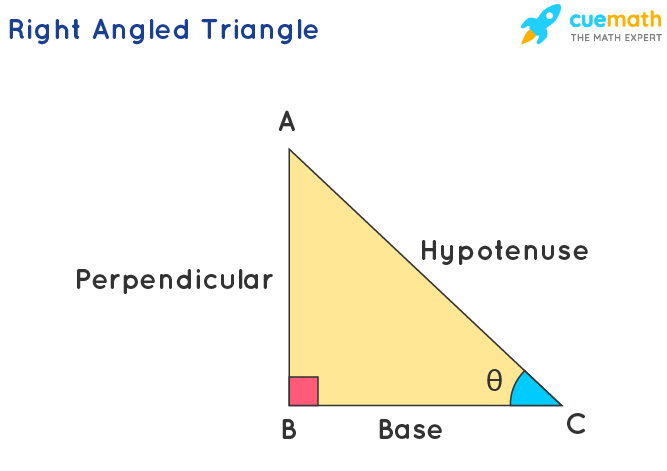
These six trigonometric ratios can be defined as,
Sine: The sine ratio for any given angle is defined as the ratio of the perpendicular to the hypotenuse. In the given triangle, sine of angle θ can be given as, sin θ = AB/AC.
Cosine: The cosine ratio for any given angle is defined as the ratio of the base to the hypotenuse. In the given triangle, cosine of angle θ can be given as, cos θ = BC/AC.
Tangent: The tangent ratio for any given angle is defined as the ratio of the perpendicular to the base. In the given triangle, the tangent of angle θ can be given as, tan θ = AB/BC.
Cosecant: The cosecant ratio for any given angle is defined as the ratio of the hypotenuse to the perpendicular. In the given triangle, cosecant of angle θ can be given as, cosec θ = AC/AB.
Secant: The secant ratio for any given angle is defined as the ratio of the hypotenuse to the base. In the given triangle, secant of angle θ can be given as, sec θ = AC/BC.
Cotangent: The cotangent ratio for any given angle is defined as the ratio of the base to the perpendicular. In the given triangle, cotangent of angle θ can be given as, cot θ = BC/AB.
Let us understand these and more trigonometric ratio formulas in detail in the next section.
Trigonometric Ratios Formulas
Trigonometric ratios can be calculated by taking the ratio of any two sides of the right-angled triangle. We can evaluate the third side using the Pythagoras theorem , given the measure of the other two sides. We can use the abbreviated form of trigonometric ratios to compare the length of any two sides with the angle in the base. The angle θ is an acute angle (θ < 90º) and in general is measured with reference to the positive x-axis, in the anticlockwise direction. The basic trigonometric ratios formulas are given below,
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
Now, let us observe the reciprocal trigonometric ratio formulas of the above-mentioned trigonometric ratios. As we observe, we notice that sin θ is a reciprocal of cosec θ, cos θ is a reciprocal of sec θ, tan θ is a reciprocal of cot θ, and vice-versa. So, the new set of formulas for trigonometric ratios is:
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
Trigonometric Ratios Table
In the trigonometric ratios table, we use the values of trigonometric ratios for standard angles 0°, 30°, 45°, 60°, and 90º. It is easy to predict the values of the table and to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles. Now, we will summarize the value of trigonometric ratios for specific angles in the table below:
Trigonometric Ratios Identities
There are many trigonometric ratios identities that we use to make our calculations easier and simpler. These include identities of complementary angles, supplementary angles, Pythagorean identities, and sum, difference, product identities.
Trigonometric Ratios of Complementary Angles Identities
The complementary angles are a pair of two angles such that their sum is equal to 90°. The complement of an angle θ is (90° - θ). The trigonometric ratios of complementary angles are:
- sin (90°- θ) = cos θ
- cos (90°- θ) = sin θ
- cosec (90°- θ) = sec θ
- sec (90°- θ) = cosec θ
- tan (90°- θ) = cot θ
- cot (90°- θ) = tan θ
Pythagorean Triogometric Ratios Identities
The Pythagorean trigonometric ratios identities in trigonometry are derived from the Pythagoras theorem. Applying Pythagoras theorem to the right-angled triangle below, we get:
Opposite 2 + Adjacent 2 = Hypotenuse 2
Dividing both sides by Hypotenuse 2
Opposite 2 /Hypotenuse 2 + Adjacent 2 /Hypotenuse 2 = Hypotenuse 2 /Hypotenuse 2
- sin 2 θ + cos 2 θ = 1
This is one of the important Pythagorean identities. In the same way, we can derive two other Pythagorean trigonometric ratios identities:
- 1 + tan 2 θ = sec 2 θ
- 1 + cot 2 θ = cosec 2 θ
Sum, Difference, Product Trigonometric Ratios Identities
The sum, difference, and product trigonometric ratios identities include the formulas of sin(A+B), sin(A-B), cos(A+B), cos(A-B), etc.
- sin (A + B) = sin A cos B + cos A sin B
- sin (A - B) = sin A cos B - cos A sin B
- cos (A + B) = cos A cos B - sin A sin B
- cos (A - B) = cos A cos B + sin A sin B
- tan (A + B) = (tan A + tan B)/ (1 - tan A tan B)
- tan (A - B) = (tan A - tan B)/ (1 + tan A tan B)
- cot (A + B) = (cot A cot B - 1)/(cot B - cot A)
- cot (A - B) = (cot A cot B + 1)/(cot B - cot A)
- 2 sin A⋅cos B = sin(A + B) + sin(A - B)
- 2 cos A⋅cos B = cos(A + B) + cos(A - B)
- 2 sin A⋅sin B = cos(A - B) - cos(A + B)
Half, Double, and Triple-Angles Trigonometric Ratios Identities
Double Angle Trigonometric Ratios Identities
The double angle trigonometric identities can be obtained by using the sum and difference formulas.
For example, from the above formula sin (A+B) = sin A cos B + cos A sin B
Substitute A = B = θ on both sides here, we get:
sin (θ + θ) = sinθ cosθ + cosθ sinθ sin 2θ = 2 sinθ cosθ
In the same way, we can derive the other double angle identities.
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos 2 θ - sin 2 θ cos 2θ = 2 cos 2 θ - 1 cos 2θ = 1 - 2 sin 2 θ cos 2θ = (1 - tan 2 θ)/(1 + tan 2 θ)
- tan 2θ = (2 tanθ)/ (1 - tan 2 θ)
- sec 2θ = sec 2 θ/(2-sec 2 θ)
- cosec 2θ = (sec θ. cosec θ)/2
- cot 2θ = (cot θ - tan θ)/2
Half Angle Trigonometric Ratios Identities
Using one of the above double angle formulas, cos 2θ = 1 - 2 sin 2 θ 2 sin 2 θ = 1- cos 2θ sin 2 θ = (1 - cos 2θ)/(2) sin θ = ±√[(1 - cos 2θ)/2]
Replacing θ by θ/2 on both sides,
sin (θ/2) = ±√[(1 - cos θ)/2]
This is the half-angle formula of sine.
In the same way, we can derive the other half-angle formulas.
- sin (θ/2) =±√[(1 - cos θ)/2]
- cos (θ/2) = ±√[(1 + cos θ)/2]
- tan (θ/2) = ±√[(1 - cos θ)(1 + cosθ)]
Triple Angle Trigonometric Ratios Identities
- sin 3θ = 3sin θ - 4sin 3 θ
- cos 3θ = 4cos 3 θ - 3cos θ
- tan 3θ = (3tanθ - tan 3 θ)/(1 - 3tan 2 θ)
Related Topics:
- Trigonometry
- Trigonometric Identities
- Trigonometric Table
- Trigonometric Formulas
Important Notes on Trigonometric Ratios:
- The values of trigonometric ratios do not change with the change in the side lengths of the triangle if the angle remains the same.
- All trigonometric functions are periodic in nature.
- Trigonometric ratios are used to find the missing sides or angles in a triangle.
Examples on Trigonometric Ratios
Example 1: In a right-angled triangle ABC, right-angled at B, hypotenuse AC = 10 units, base BC = 8 units and perpendicular AB = 6 units and if ∠ACB = θ, then find the trigonometric ratios tan θ, sin θ, and cos θ.
We know, sin θ = perpendicular/hypotenuse
cos θ = base/hypotenuse
tan θ = perpendicular/base
⇒ sin θ = 6/10 = 3/5
⇒ cos θ = 8/10 = 4/5
⇒ tan θ = 6/8 = 3/4
Answer: sin θ, cos θ, and tan θ for the given triangle are 3/5, 4/5, and 3/4 respectively.
Example 2: A building is at a distance of 210 feet from point A on the ground. Find the height of the building if tan θ = 4/3?
Solution: The triangle formed is a right-angled triangle. Now apply the trigonometric ratio of tanθ to calculate the height of the building.
4/3 = Height/210 ft
Height = (4 × 210/3) = 280 ft
Answer: The height of the building is 280 ft.
Example 3: The triangle is right-angled at C with AB = 29 units and AC = 20 units. Can you verify the trigonometric ratios identity cos 2 θ + sin 2 θ = 1 using these values?
Solution: We will find BC using the Pythagorean theorem,
BC = √(AB 2 - AC 2 )
= √(29 2 - 20 2 )
= √841 2 - 400 2 )
Now let's determine the values of sinθ and cosθ
sinθ = AC/AB = 20/29
cosθ = BC/AB = 21/29
Now let's verify the identity.
cos 2 θ + sin 2 θ = (21/29) 2 + (20/29) 2 = (400 + 441)/841 = 1
Answer: Hence, the trigonometric ratios identity is verified.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Trigonometric Ratios
go to slide go to slide
FAQs on Trigonometric Ratios
How to find trigonometric ratios.
Trigonometric Ratios can be calculated either by using the given acute angle or determining the ratios of the sides of the right-angled triangle. The trigonometric ratios formulas to be used are:
What are the Six Trigonometric Ratios?
The main six trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. The trigonometric ratios can be calculated using the formulas given in the article.
What are the Applications of Trigonometric Ratios?
There are various applications of trigonometric ratios such as:
- Sine and cosine are used to represent sound waves.
- Some trigonometric ratios are used in the field of architecture, constructing buildings, etc.
- They are used in creating maps.

What are Trigonometric Ratios of Specific Angles?
Trigonometric ratios can be determined for different angles. But for convenience of calculations, we memorize the trigonometric ratios of some specific angles like 0°, 30°, 45°, 60°, 90°. Refer to the trigonometric ratios table for the values of the ratios at these angles.
What are Trigonometric Ratios of Complementary Angles?
Complementary angles are two angles whose sum is 90°. Formulas for trigonometric ratios of complementary angles are:
What is the Relationship Between Sin, Cos, and Tan Trigonometric Ratios?
We know, that sin can be given as perpendicular/hypotenuse, cos as base/hypotenuse, and tan as perpendicular/base. The relationship between the trigonometric ratios sin, cos, and tan can therefore be given as, tan θ = sin θ/cos θ.
Trigonometric Ratios
These lessons, with videos, examples and step-by-step solutions, help GCSE/IGCSE Maths students learn about the trigonometric ratios: sine, cosine, tangent, secant, cosecant, and cotangent.
Related Pages Trigonometric Graphs Trigonometric Functions Lessons On Trigonometry More GCSE Math Lessons Math Worksheets
The following diagram shows the six trig ratios: Sin, Cos, Tan, Sec, Csc, and Cot. Scroll down the page for more examples and solutions on the trigonometric ratios.
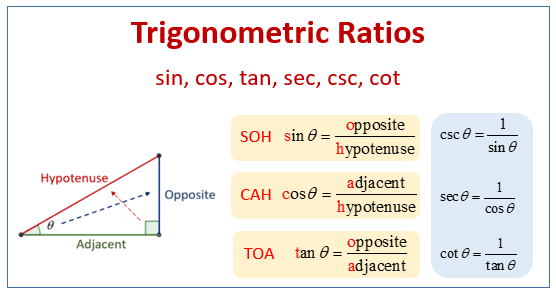
Six Trig Ratios: sin, cos, tan, csc, sec, and tan
Example: Determine the six trigonometric ratios for angle A in the right triangle.
Trigonometry - Right Angled Triangles - Naming the Sides In this tutorial you are shown how to name the sides of any right-angled triangle which is the first stage in solving a question in trigonometry.
Trigonometry - The Trig Ratios In this tutorial you are shown how the sin, cos and tan ratios compare two sides of a right-angled triangle. You need to know this before calculating lengths and angles of right-angled triangles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
PROBLEMS ON TRIGONOMETRIC RATIOS
Problem 1 :
For the measures in the figure shown below, compute sine, cosine and tangent ratios of the angle θ.
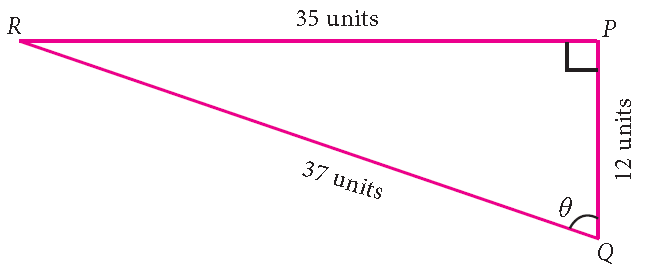
In the given right angled triangle, note that for the given angle θ, PR is the ‘opposite’ side and PQ is the ‘adjacent’ side.
Then,
sin θ = opposite side/hypotenuse = PR/QR = 35/37
cos θ = adjacent side/hypotenuse = PQ/QR = 12/37
tan θ = opposite side / adjacent side = PR/PQ = 35/12
Problem 2 :
Find the six trigonometric ratios of the angle θ using the diagram shown below.
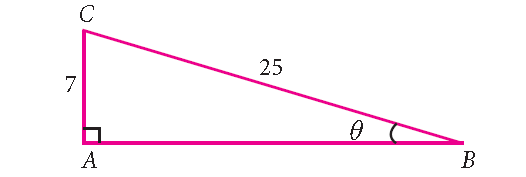
In the given right angled triangle, note that for the given angle θ, AC is the ‘opposite’ side and AB is the ‘adjacent’ side.
And also, the length of the adjacent side 'AB' is not given.
Find the length of AB.
By Pythagorean Theorem,
BC 2 = AB 2 + AC 2
25 2 = AB 2 + 7 2
625 = AB 2 + 49
Subtract 49 from each side.
576 = AB 2
24 2 = AB 2
24 = AB
sin θ = opposite side/hypotenuse = AC/ BC = 7/25
cos θ = adjacent side/hypotenuse = AB/BC = 24/25
tan θ = opposite side/adjacent side = AC/AB = 7/24
csc θ = 1/s in θ = 25/7
sec θ = 1/cos θ = 25/24
cot θ = 1/tan θ = 24/7
Problem 3 :
If tanA = 2/3, then find all the other trigonometric ratios.
tanA = opposite side/adjacent side = 2/3
AC 2 = AB 2 + BC 2
AC 2 = 3 2 + 2 2
AC 2 = 9 + 4
AC 2 = 13
AC = √13
sinA = opposite side/hypotenuse = BC/ AC = 2/ √ 13
cosA = adjacent side/hypotenuse = AB/AC = 3/ √13
cscA = 1/s inA = √13 /2
secA = 1/cosA = √13 /3
cotA = 1/tanA = 3/2
Problem 4 :
If sec θ = 2/3, then find the value of
(2sinθ - 3cosθ)/(4sinθ - 9cosθ)
sec θ = hypotenuse/adjacent side = 13/5
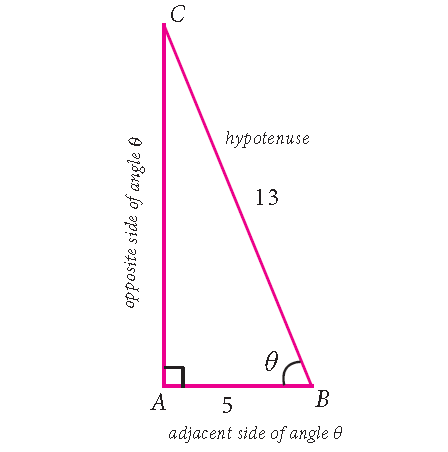
13 2 = 5 2 + AC 2
169 = 25 + AC 2
Subtract 25 from each side.
144 = AC 2
12 2 = AC 2
12 = AC
sin θ = opposite side/hypotenuse = AC/BC = 12/1 3
cos θ = adjacent side/hypotenuse = AB/BC = 5/ 13
(2sinθ - 3cosθ)/(4sinθ - 9cosθ) :
= (2 ⋅ 12/13 - 3 ⋅ 5/13)/(4 ⋅ 12/13 - 9 ⋅ 5/13)
= (24 /13 - 1 5/13)/(48 /13 - 45/13)
= [(24 - 15)/13]/[(48 - 45)/13]
= (9/13)/(3/13)
= (9/13) ⋅ (13/3)
= 9/3
(2sinθ - 3cosθ)/(4sinθ - 9cosθ) = 3
To learn SOHCAHTOA in detail,
please click here
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Digital sat math problems and solutions (part - 10).
Aug 29, 24 10:09 PM
Digital SAT Math Problems and Solutions (Part - 9)
Aug 29, 24 07:03 PM
Digital SAT Math Problems and Solutions (Part - 8)
Aug 29, 24 06:57 PM
- Math Article
Trigonometric Ratios

The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec). In geometry, trigonometry is a branch of mathematics that deals with the sides and angles of a right-angled triangle. Therefore, trig ratios are evaluated with respect to sides and angles.
The trigonometry ratios for a specific angle ‘θ’ is given below:
| Sin θ | Opposite Side to θ/Hypotenuse |
| Cos θ | Adjacent Side to θ/Hypotenuse |
| Tan θ | Opposite Side/Adjacent Side & Sin θ/Cos θ |
| Cot θ | Adjacent Side/Opposite Side & 1/tan θ |
| Sec θ | Hypotenuse/Adjacent Side & 1/cos θ |
| Cosec θ | Hypotenuse/Opposite Side & 1/sin θ |
Note: Opposite side is the perpendicular side and the adjacent side is the base of the right-triangle. Also, check out trigonometric functions to learn about each of these ratios or functions in detail. Trigonometric Identities
Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle. The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle .
The three sides of the right triangle are:
- Hypotenuse (the longest side)
- Perpendicular (opposite side to the angle)
- Base (Adjacent side to the angle)
Related Articles:
- Trigonometric Identities
- Trigonometric Ratios of Complementary Angles
- Trigonometric Ratios Of Standard Angles
- Trigonometry Angles
- Trigonometry Formulas
- Trigonometry Values
How to Find Trigonometric Ratios?
Consider a right-angled triangle, right-angled at B.
With respect to ∠C, the ratios of trigonometry are given as:
- sine: Sine of an angle is defined as the ratio of the side opposite(perpendicular side) to that angle to the hypotenuse.
- cosine: Cosine of an angle is defined as the ratio of the side adjacent to that angle to the hypotenuse.
- tangent: Tangent of an angle is defined as the ratio of the side opposite to that angle to the side adjacent to that angle.
- cosecant: Cosecant is a multiplicative inverse of sine.
- secant: Secant is a multiplicative inverse of cosine.
- cotangent: Cotangent is the multiplicative inverse of the tangent.
The above ratios are abbreviated as sin, cos, tan, cosec, sec and tan respectively in the order they are described. So, for Δ ABC , the ratios are defined as:
sin C = ( Side opposite to ∠C)/(Hypotenuse) = AB/AC
cos C = ( Side adjacent to ∠C)/(Hypotenuse) = BC/AC
tan C = ( Side opposite to ∠C)/(Side adjacent to ∠C) = AB/BC = sin ∠C/cos ∠C
cosec C = 1/sin C = ( Hypotenuse)/ (Side Opposite to ∠C) = AC/AB
sec C = 1/cos C = ( Hypotenuse)/ (Side Opposite to ∠C) = AC/BC
cot C = 1/tan C = ( Side adjacent to ∠C)/(Side opposite to ∠C) = BC/AB
In right Δ ABC, if ∠ A and ∠ C are assumed as 30° and 60° , then there can be infinite right triangles with those specifications but all the ratios written above for ∠ C in all of those triangles will be same. So, all the ratios for any of the acute angles (either ∠ A or ∠ C ) will be the same for every right triangle. This means that the ratios are independent of lengths of sides of the triangle.
Trigonometric Ratios Table
The trigonometric ratios for some specific angles such as 0 °, 30 °, 45 °, 60 ° and 90° are given below, which are commonly used in mathematical calculations.
| Sin C | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos C | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tan C | 0 | 1/√3 | 1 | √3 | ∞ |
| Cot C | ∞ | √3 | 1 | 1/√3 | 0 |
| Sec C | 1 | 2/√3 | √2 | 2 | ∞ |
| Cosec C | ∞ | 2 | √2 | 2/√3 | 1 |
From this table, we can find the value for the trigonometric ratios for these angles. Examples are:
- Sin 30° = ½
- Cos 90° = 0
- Tan 45° = 1
Trigonometry Applications
Trigonometry is one of the most important branches of mathematics. Some of the applications of trigonometry are:
- Measuring the heights of towers or big mountains
- Determining the distance of the shore from the sea
- Finding the distance between two celestial bodies
- Determining the power output of solar cell panels at different inclinations
- Representing different physical quantities such as mechanical waves, electromagnetic waves, etc.
It is evident from the above examples that trigonometry has its involvement in a major part of our day-to-day life and much more. In most of the applications listed above, something was being measured and that is what trigonometry is all about.
Solved Problems
Q.1: If in a right-angled triangle ABC, right-angled at B, hypotenuse AC = 5cm, base BC = 3cm and perpendicular AB = 4cm and if ∠ACB = θ, then find tan θ, sin θ and cos θ.
Sol: Given,
Hypotenuse, AC = 5cm
Base, BC = 3cm
Perpendicular, AB = 4cm
tan θ = Perpendicular/Base = 4/3
Sin θ = Perpendicular/Hypotenuse = AB/AC = ⅘
Cos θ = Base/Hypotenuse = BC/AC = ⅗
Q.2: Find the value of tan θ if sin θ = 12/5 and cos θ = ⅗.
Sol: Given, sin θ = 12/5 and cos θ = ⅗
As we know,
Tan θ = Sin θ/Cos θ
Tan θ = (12/5)/(⅗)
Tan θ = 12/3
Practice Questions
- Find the value of sin θ, if tan θ = ¾ and cos θ = ½.
- Find tan θ if sin θ = 4/3 and cos θ = 3/2
- Find sec θ, if cos θ = 9/8
- Find cosec θ, if sin θ 16/5
Video Lesson
Trigonometric ratios of compound angles.

Frequently Asked Questions – FAQs
What are the three primary trigonometric ratios, what are the six trigonometric ratios, what is soh cah toa, what is the formula for cotangent, secant and cosecant, what is the relationship between sin, cos and tan.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
Tnks for this! Very informative!
The explanation of trigonometric ratios is given very neat and illustrative. It is easy to understand and difficult to forget.
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Sine, Cosine and Tangent
Three Functions, but same idea.
Right Triangle
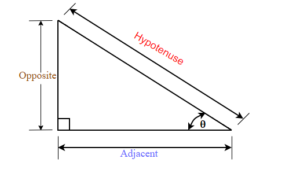
Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle .
Before getting stuck into the functions, it helps to give a name to each side of a right triangle:
- "Opposite" is opposite to the angle θ
- "Adjacent" is adjacent to (next to) the angle θ
- "Hypotenuse" is the long one
Opposite is always opposite the angle
And Adjacent is always next to the angle
Sine , Cosine and Tangent (often shortened to sin , cos and tan ) are each a ratio of sides of a right angled triangle:
For a given angle θ each ratio stays the same no matter how big or small the triangle is
To calculate them:
Divide the length of one side by another side
Example: What is the sine of 35°?
Using this triangle (lengths are only to one decimal place):
| sin(35°) | = |
| = | |
| = | |
| cos(35°) | = |
| = | |
| = | |
| tan(35°) | = |
| = | |
| = |
Size Does Not Matter
The triangle can be large or small and the ratio of sides stays the same .
Only the angle changes the ratio.
Try dragging point "A" to change the angle and point "B" to change the size:

Good calculators have sin, cos and tan on them, to make it easy for you. Just put in the angle and press the button.
But you still need to remember what they mean !
In picture form:
Practice Here:
How to remember? Think "Sohcahtoa" !
It works like this:
| ine = pposite / ypotenuse | |
| osine = djacent / ypotenuse | |
| angent = pposite / djacent |
You can read more about sohcahtoa . Remember it, as it may help in an exam !
Angles From 0° to 360°
Move the mouse around to see how different angles (in radians or degrees ) affect sine, cosine and tangent.
In this animation the hypotenuse is 1, making the Unit Circle .
Notice that the adjacent side and opposite side can be positive or negative, which makes the sine, cosine and tangent change between positive and negative values also.
| and go to the party?" "... just !" |
Example: what are the sine, cosine and tangent of 30° ?
The classic 30° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of√ 3 :
Now we know the lengths, we can calculate the functions:
| sin(30°) = 1 / 2 = 0.5 | ||
| cos(30°) = 1.732 / 2 = 0.866... | ||
| tan(30°) = 1 / 1.732 = 0.577... |
(get your calculator out and check them!)
Example: what are the sine, cosine and tangent of 45° ?
The classic 45° triangle has two sides of 1 and a hypotenuse of √ 2 :
| sin(45°) = 1 / 1.414 = 0.707... | ||
| cos(45°) = 1 / 1.414 = 0.707... | ||
| tan(45°) = 1 / 1 = 1 |
Why are these functions important?
- Because they let us work out angles when we know sides
- And they let us work out sides when we know angles
Example: Use the sine function to find "d"
- The cable makes a 39° angle with the seabed
- The cable has a 30 meter length .
And we want to know "d" (the distance down).
The depth "d" is 18.88 m
Try this paper-based exercise where you can calculate the sine functionfor all angles from 0° to 360°, and then graph the result. It will help you to understand these relativelysimple functions.
You can also see Graphs of Sine, Cosine and Tangent .
And play with a spring that makes a sine wave .
Less Common Functions
To complete the picture, there are 3 other functions where we divide one side by another, but they are not so commonly used.
They are equal to 1 divided by cos , 1 divided by sin , and 1 divided by tan :
| Secant Function: | ) = | |||
| Cosecant Function: | ) = | |||
| Cotangent Function: | ) = |
HIGH SCHOOL
- ACT Tutoring
- SAT Tutoring
- PSAT Tutoring
- ASPIRE Tutoring
- SHSAT Tutoring
- STAAR Tutoring
GRADUATE SCHOOL
- MCAT Tutoring
- GRE Tutoring
- LSAT Tutoring
- GMAT Tutoring
- AIMS Tutoring
- HSPT Tutoring
- ISAT Tutoring
- SSAT Tutoring
Search 50+ Tests
Loading Page
math tutoring
- Elementary Math
- Pre-Calculus
- Trigonometry
science tutoring
Foreign languages.
- Mandarin Chinese
elementary tutoring
- Computer Science
Search 350+ Subjects
- Video Overview
- Tutor Selection Process
- Online Tutoring
- Mobile Tutoring
- Instant Tutoring
- How We Operate
- Our Guarantee
- Impact of Tutoring
- Reviews & Testimonials
- About Varsity Tutors
Trigonometry : Solving Word Problems with Trigonometry
Study concepts, example questions & explanations for trigonometry, all trigonometry resources, example questions, example question #1 : solving word problems with trigonometry.

You can draw the following right triangle using the information given by the question:

Since you want to find the height of the platform, you will need to use tangent.

You can draw the following right triangle from the information given by the question.

In order to find the height of the flagpole, you will need to use tangent.

You can draw the following right triangle from the information given in the question:

In order to find out how far up the ladder goes, you will need to use sine.

In right triangle ABC, where angle A measures 90 degrees, side AB measures 15 and side AC measures 36, what is the length of side BC?

This triangle cannot exist.

Example Question #5 : Solving Word Problems With Trigonometry
A support wire is anchored 10 meters up from the base of a flagpole, and the wire makes a 25 o angle with the ground. How long is the wire, w? Round your answer to two decimal places.
23.81 meters

28.31 meters
21.83 meters
To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25 o , the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w.
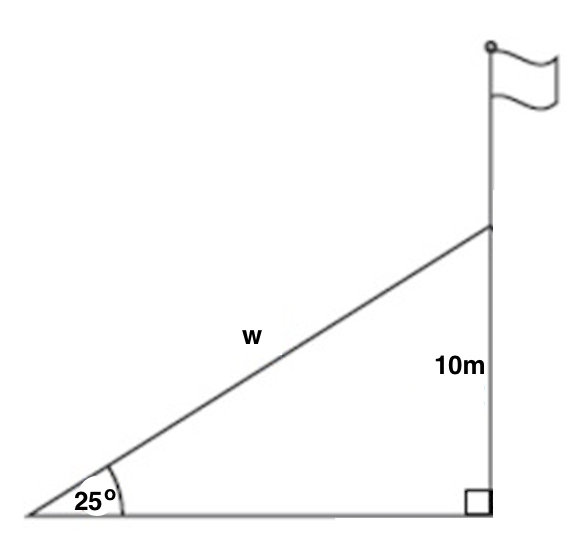
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25 o . 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.
We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:

To solve this problem instead using the cosecant function, we would get:

The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem.

Example Question #6 : Solving Word Problems With Trigonometry
When the sun is 22 o above the horizon, how long is the shadow cast by a building that is 60 meters high?
To solve this problem, first set up a diagram that shows all of the info given in the problem.
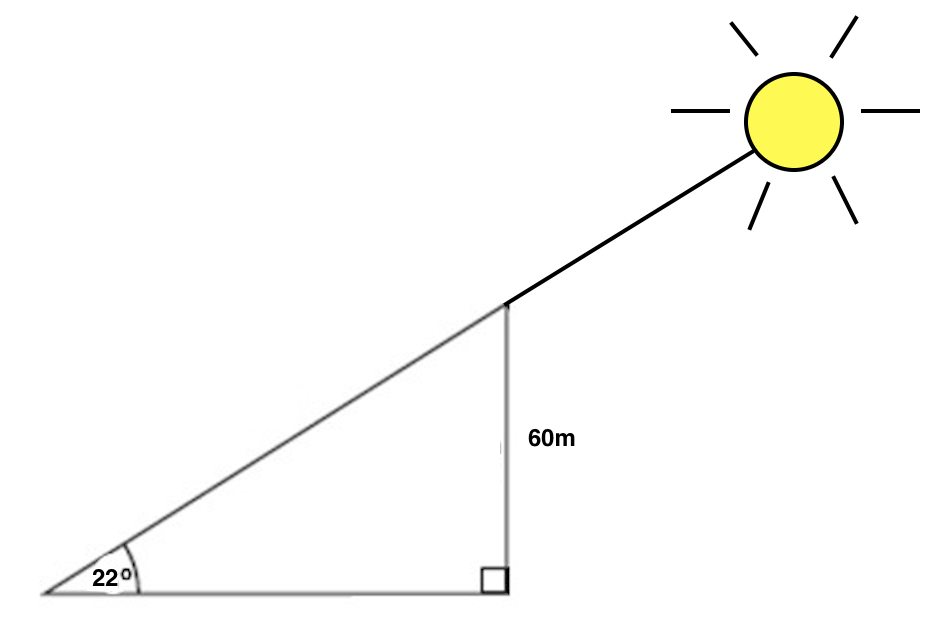
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.

Therefore the shadow cast by the building is 150 meters long.
If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)
Example Question #7 : Solving Word Problems With Trigonometry
From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19 o . How far from the boat is the top of the lighthouse?
423.18 meters
318.18 meters
36.15 meters
110.53 meters
To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.
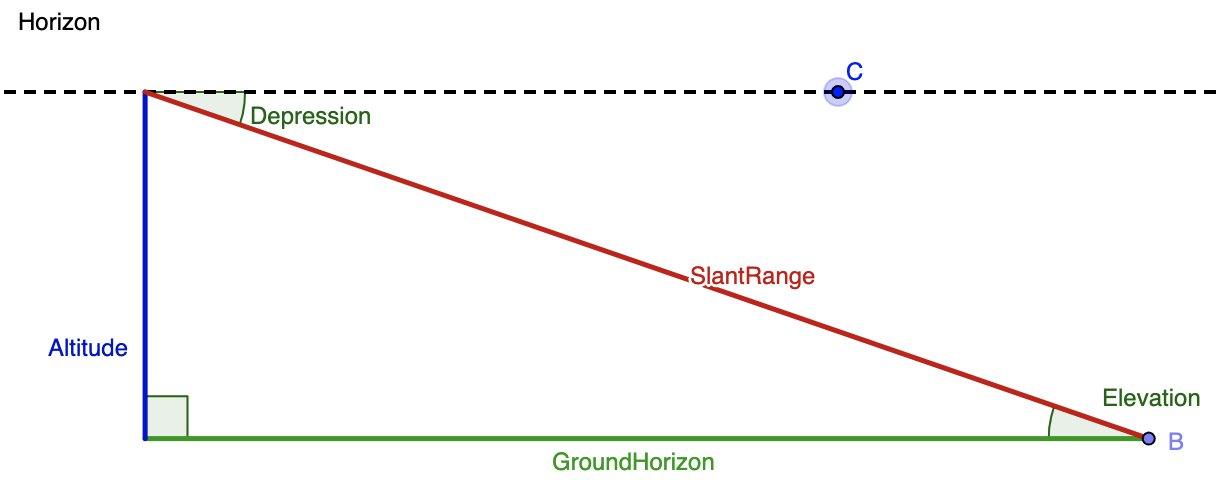
Merging together the given info and this diagram, we know that the angle of depression is 19 o and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:

Example Question #8 : Solving Word Problems With Trigonometry
Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined 22 o to the horizontal, how high above her starting point is she when she arrives at the lookout?
9.37 meters
1480 meters
3708.74 meters
10677.87 meters
1616.1 meters
As with other trig problems, begin with a sketch of a diagram of the given and sought after information.
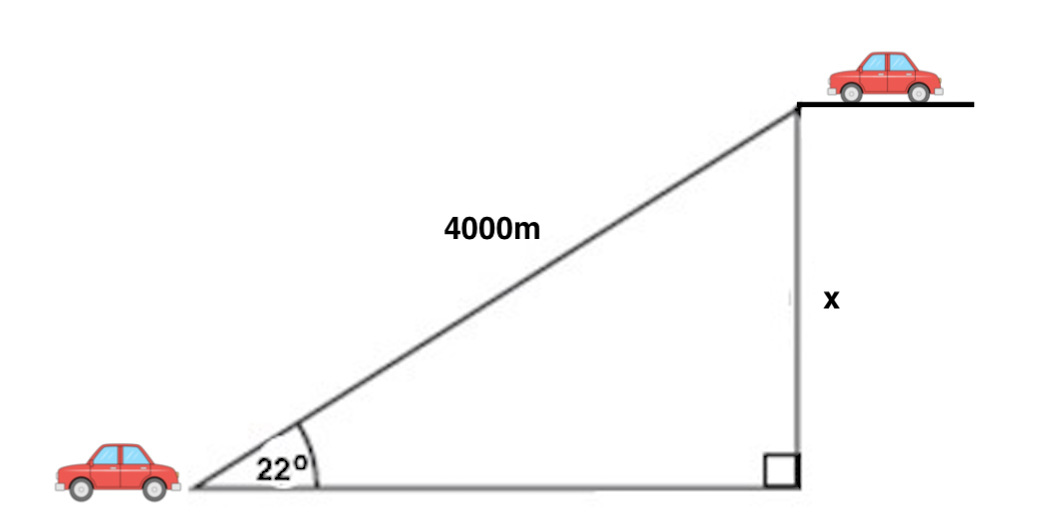
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is 22 o . Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled x in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:

Therefore the change in height between Angelina's starting and ending points is 1480 meters.
Example Question #9 : Solving Word Problems With Trigonometry
Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48 o . How high is the taller building?
To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.
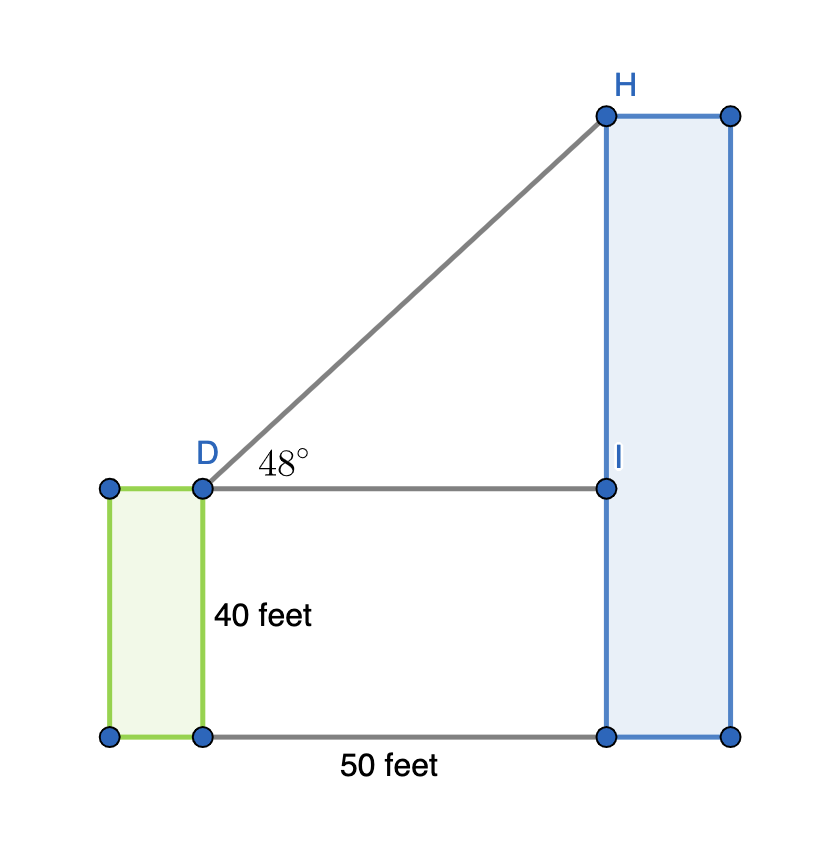
Example Question #10 : Solving Word Problems With Trigonometry
Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32 o . How high is the taller building?
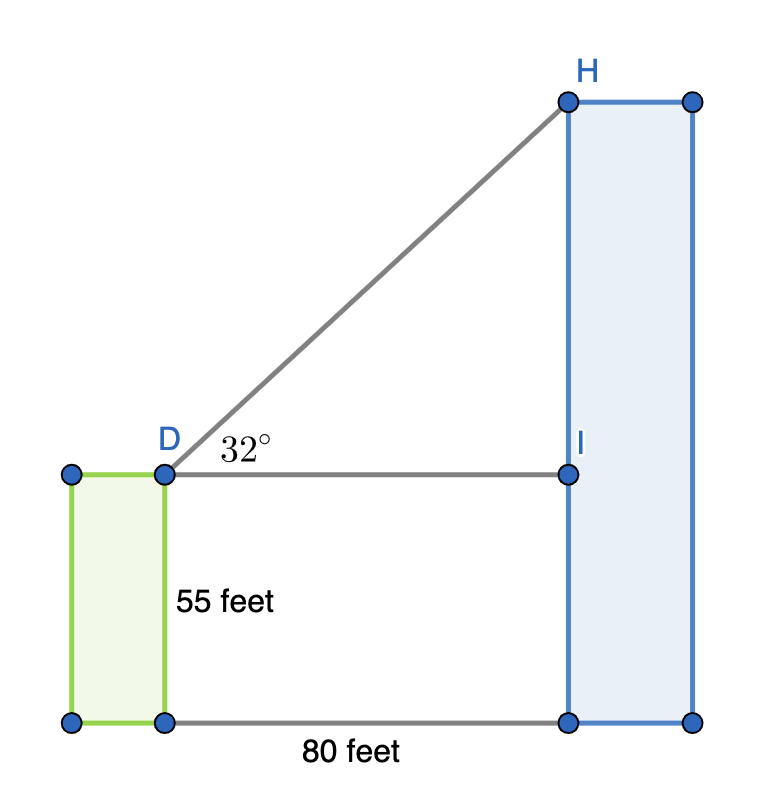
Report an issue with this question
If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.
DMCA Complaint
If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.
Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.
Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.
Please follow these steps to file a notice:
You must include the following:
A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.
Send your complaint to our designated agent at:
Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105
Or fill out the form below:
Contact Information
Complaint details.

| Email address: | |
| Your name: | |
| Feedback: |

COMMENTS
Problems on Trigonometric Ratios. Some trigonometric solutions based problems on trigonometric ratios are shown here with the step-by-step explanation. 1. If sin θ = 8/17, find other trigonometric ratios of <θ. Let us draw a ∆ OMP in which ∠M = 90°. Then sin θ = MP/OP = 8/17. Let MP = 8k and OP = 17k, where k is positive.
Answers - Version 1. Answers - Version 2. The Corbettmaths Practice Questions on Trigonometry.
Solution to Problem 1: First we need to find the hypotenuse using Pythagora's theorem. (hypotenuse) 2 = 8 2 + 6 2 = 100. and hypotenuse = 10. We now use the definitions of the six trigonometric ratios given above to find sin A, cos A, tan A, sec A, csc A and cot A. sin A = side opposite angle A / hypotenuse = 8 / 10 = 4 / 5.
b) tan 41° = 1.9/x. c) tan θ = 11/8. Show Video Lesson. Applications of Trigonometric Ratios (Word Problems Involving Tangent, Sine and Cosine) Examples: Find the area of the parallelogram. A 70 foot ramp rises from the first floor to the second floor of a parking garage. The ramp makes an angle with the ground.
Trigonometric ratios are frequently expressed as decimal approximations. Example 2 : Find the sine, the cosine, and the tangent of the indicated angle. a. ∠S b. ∠R. Solution (a) : The length of the hypotenuse is 13. For ∠ S, the length of the opposite side is 5, and the length of the adjacent side is 12.
How to find trigonometry ratios sine, cosine, and tangent. Trig Ratios. Free Printable and Online Worksheet with answers. opposite, adjacent and hypotenuse. Practice Worksheets for Geometry and Trigonometry. ... Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own ...
Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. Identify what we are looking for.; Label what we are looking for by choosing a variable to represent it.; Find the required trigonometric ratio.; Solve the ratio using good algebra techniques.; Check the answer by substituting it back into the ratio in step 4 and by making ...
3. The exterior angle is not equal to the sum of the opposite interior angles. 5. The sum of the acute angles is not 90 ∘. 7. The largest side is not opposite the largest angle. 9. The Pythagorean theorem is not satisfied. 11. 52 + 122 = 132, but the angle opposite the side of length 13 is 85 ∘.
How To Solve Trigonometry Problems Or Questions? Step 1: If no diagram is given, draw one yourself. Step 2: Mark the right angles in the diagram. ... This video shows how to use the trigonometric ratio, sine, to find the elevation gain of a hiker going up a slope. Example: A hiker is hiking up a 12 degrees slope. ...
Trigonometric Ratios Identities. Several trigonometric ratios identities make our calculations simpler such as: sin 2 θ + cos 2 θ = 1; 1 + tan 2 θ = sec 2 θ; 1 + cot 2 θ = cosec 2 θ; There are also some variations of the above 3 identities, which are nothing but rearranging the ones given above.
Free math problem solver answers your trigonometry homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app. Start 7-day free trial on the app. Download free on Amazon. Download free in Windows Store. Take a photo of your math problem on the app. get Go. Trigonometry.
Trigonometry questions given here involve finding the missing sides of a triangle with the help of trigonometric ratios and proving trigonometry identities. We know that trigonometry is one of the most important chapters of Class 10 Maths. Hence, solving these questions will help you to improve your problem-solving skills. What is Trigonometry?
1 Use measurements to calculate the trigonometric ratios for acute angles #1-10, 57-60. 2 Use trigonometric ratios to find unknown sides of right triangles #11-26. 3 Solve problems using trigonometric ratios #27-34, 41-46. 4 Use trig ratios to write equations relating the sides of a right triangle #35-40.
Trigonometric Ratios Worksheets - Grab our free math worksheets featuring exercises in mathematics to ace the problem-solving methods of different mathematical topics. Grade. KG. 1st. 2nd. 3rd. 4th. 5th. 6th. 7th. 8th. Algebra 1. Algebra 2. ... By solving Trigonometric ratios worksheets, you'll understand that the trigonometric ratios are given ...
The six trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. Learn how to use these ratios to solve problems in this free lesson!
In trigonometry, there are six trigonometric ratios, namely, sine, cosine, tangent, secant, cosecant, and cotangent.These ratios are written as sin, cos, tan, sec, cosec(or csc), and cot in short. Let us have a look at the right-angled triangle shown below. Trigonometric ratios can be used to determine the ratios of any two sides out of a total of three sides of a right-angled triangle in ...
These lessons, with videos, examples and step-by-step solutions, help GCSE/IGCSE Maths students learn about the trigonometric ratios: sine, cosine, tangent, secant, cosecant, and cotangent. The following diagram shows the six trig ratios: Sin, Cos, Tan, Sec, Csc, and Cot. Scroll down the page for more examples and solutions on the trigonometric ...
PROBLEMS ON TRIGONOMETRIC RATIOS. Problem 1 : For the measures in the figure shown below, compute sine, cosine and tangent ratios of the angle θ. Solution : In the given right angled triangle, note that for the given angle θ, PR is the 'opposite' side and PQ is the 'adjacent' side. Then,
Our mission is to provide a free, world-class education to anyone, anywhere. Khan Academy is a 501 (c) (3) nonprofit organization. Donate or volunteer today! About. News.
If this problem persists, tell us. Our mission is to provide a free, world-class education to anyone, anywhere. Khan Academy is a 501(c)(3) nonprofit organization. Donate or volunteer today! Site Navigation. About. News; Impact; Our team; Our interns; Our content specialists; Our leadership; Our supporters; Our contributors; Our finances;
Trigonometric Ratios. The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec). In geometry, trigonometry is a branch of mathematics that deals with the sides and angles of a right-angled triangle. Therefore, trig ratios are evaluated with respect to sides and angles.
Sine, Cosine and Tangent. Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle:. For a given angle θ each ratio stays the same no matter how big or small the triangle is. To calculate them: Divide the length of one side by another side
Correct answer: 23.81 meters. Explanation: To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25 o, the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w. Now, we just need to solve for w using the information given in the diagram.