| Groups Have Equal Variance (default) | | Groups Have Unequal Variance (Welch t-test) | | Two Tailed Test (default) | | One Tailed Test | | 0.05 (default) | | 0.01 | | 0.001 | | Unpaired T Test (default) | | Paired (Dependent) T Test | - Long Division
- Evaluate Expressions
- Fraction Calculator
- Greatest Common Divisor GCD
- Least Common Multiple LCM
- Prime Factorization
- Scientific Notation
- Percentage Calculator
- Dec / Bin / Hex
- Factoring Polynomials
- Polynomial Roots
- Synthetic Division
- Polynomial Operations
- Graphing Polynomials
- Simplify Polynomials
- Generate From Roots
- Simplify Expression
- Multiplication / Division
- Addition / Subtraction
- Rationalize Denominator
- Simplifying
- Quadratic Equations Solver
- Polynomial Equations
- Solving Equations - With Steps
- Solving (with steps)
- Quadratic Plotter
- Factoring Trinomials
- Equilateral Triangle
- Right Triangle
- Oblique Triangle
- Square Calculator
- Rectangle Calculator
- Circle Calculator
- Hexagon Calculator
- Rhombus Calculator
- Trapezoid Calculator
- Triangular Prism
- Distance calculator
- Midpoint Calculator
- Triangle Calculator
- Graphing Lines
- Lines Intersection
- Two Point Form
- Line-Point Distance
- Parallel/Perpendicular
- Circle Equation
- Circle From 3 Points
- Circle-line Intersection
- Modulus, inverse, polar form
- Vectors (2D & 3D)
- Add, Subtract, Multiply
- Determinant Calculator
- Matrix Inverse
- Characteristic Polynomial
- Eigenvalues
- Eigenvectors
- Matrix Decomposition
- Limit Calculator
- Derivative Calculator
- Integral Calculator
- Arithmetic Sequences
- Geometric Sequences
- Find n th Term
- Degrees to Radians
- Trig. Equations
- Probability Calculator
- Probability Distributions
- Descriptive Statistics
- Standard Deviation
- Z - score Calculator
- Normal Distribution
- T-Test Calculator
- Correlation & Regression
- Simple Interest
- Compound Interest
- Amortization Calculator
- Annuity Calculator
- Work Problems
Hire MATHPORTAL experts to do math homework for you. Prices start at $3 per problem. Twelve younger adults and twelve older adults conducted a life satisfaction test. The data are presented in the table below. Compute the appropriate t-test. Are the means between two data sets are significantly different at level $\alpha < 0.05$. Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas . If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected] Email (optional) Two sample t test Kruskal wallis Pearson product moment Two sample f test One way anova Bartlett test Chi square goodness of fit Fligner killeen Hypothesis Test CalculatorUpload your data set below to get started Or input your data as csv Sharing helps us build more free tools For optimal use, please visit DATAtab on your desktop PC! Metric Variables:Ordinal variables:, nominal variables:, hypothesis test calculator. Do you want to calculate a hypothesis test such as a t-test , Chi Square test or an ANOVA ? You can do that easily here in the browser.  If you want to use your own data just clear the upper table - Clear the table in the Hypothesis test calculator.
- Copy your data into the table.
- Select the variables.
In the hypothesis test calculator you can calculate e.g. a t-test, a chi-square test, a binomial test or an analysis of variance. If you need a more detailed explanation, you can find more information in the tutorials. In order to use the hypothesis test calculator, you must first formulate your hypothesis and collect your data. DATAtab will then suggest the hypothesis test you need based on the data entered into the statistics calculator. p value calculatorWith the p value calculator you can calculate the p value for different tests. There is a wide range of methods for this. Just click on the variables you want to evaluate above and DATAtab will give you the tests you can use. For example, if you select a metric and a categorical variable, the Independent t-Test calculator is automatically selected. If your data is not normally distributed, simply use the Mann-Whitney U-test calculator. H0 and H1 calculatorWith the h0 and h1 calculator for the different hypothesis test you can calculate the p-value which gives you an indication if you can reject the H0 or not. Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net Descriptive StatisticsHypothesis test, independent t-test calculator. To calculate an independent t-Test online just select one metric Variable and one nominal Variable with two values. 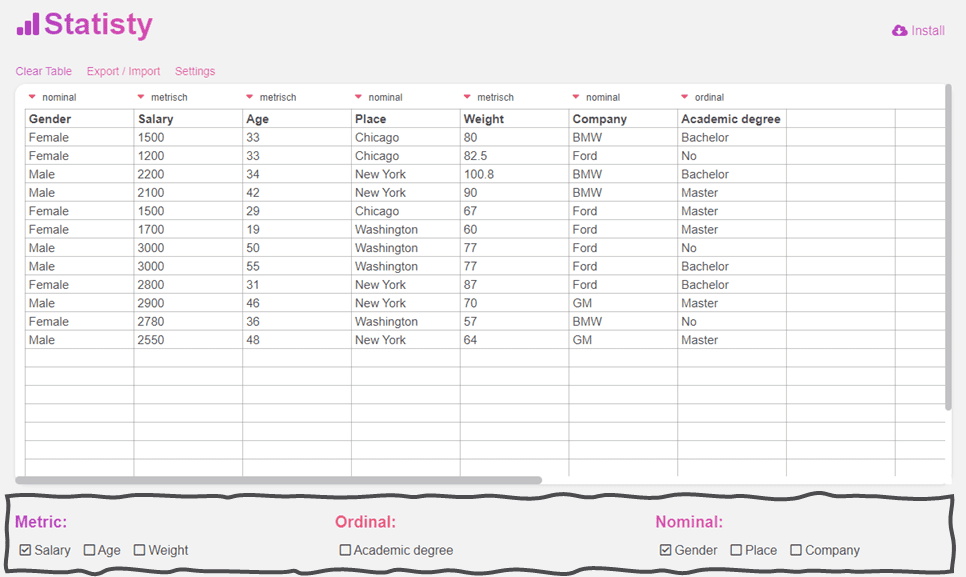 If you want to use your own data, just copy your data into the upper table and make sure that the variable name is in the first row. The results of independent t tests are then displayed clearly. 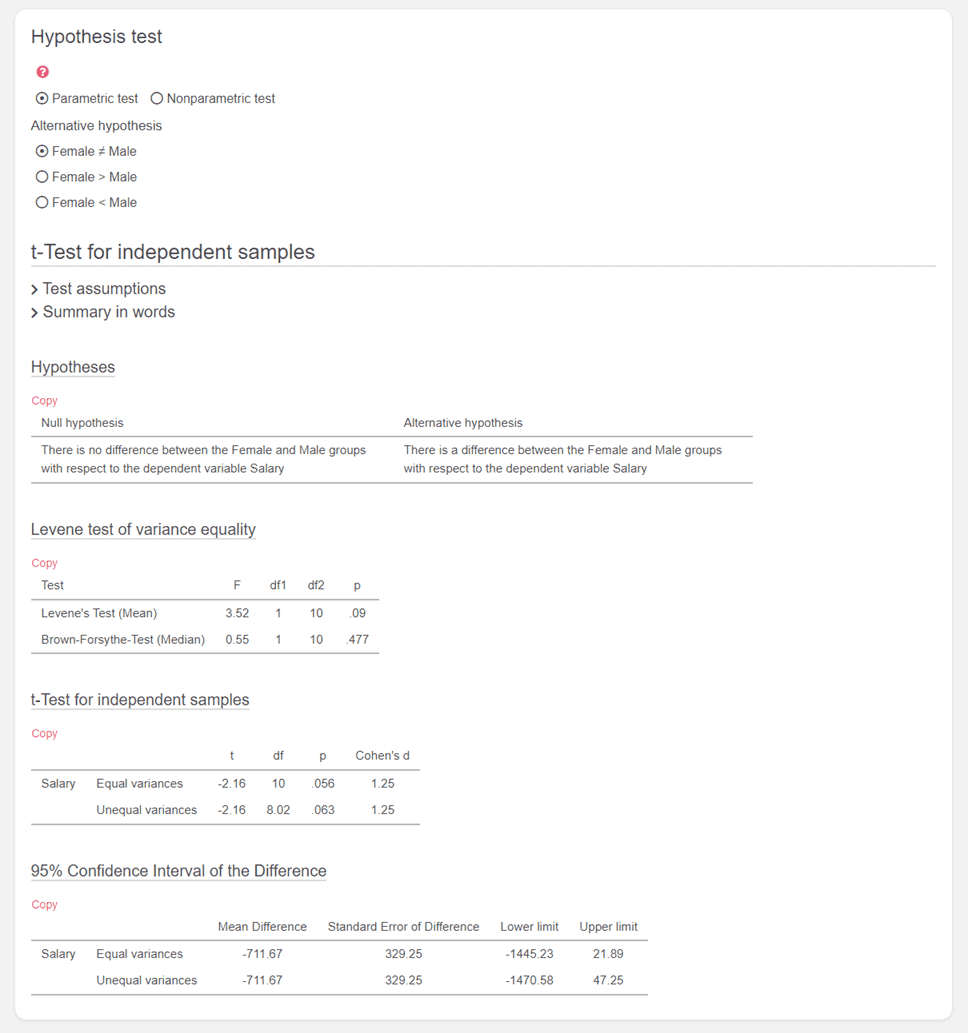 At the beginning of the independent t-test calculator you can choose what your alternative hypothesis is. Then you can test the assumptions for the t-test and you will get the null and alternative hypotheses. Then you get the relative results. Independent t-TestAn independent t-test is a statistical hypothesis test that is used to determine if there is a significant difference between the means of two independent groups or conditions. It is based on the t-distribution, which is a probability distribution that takes into account the sample size and the variability of the data. The t-test works by comparing the t-value, which is a measure of the difference between the means, to a critical value based on the desired level of significance (usually denoted as α). The critical value is determined by the degrees of freedom, which depend on the sample sizes of the groups being compared. If your data are not normally distributed and therefore do not meet the requirements for the independent t-test, you can simply calculate the Mann-Whitney U test online . Independent T-test HypothesesIn the independent t-test (also known as the independent samples t-test or two-sample t-test), we compare the means of two independent groups to see if there is a statistically significant difference between them. The hypotheses for the independent t-test are:- Null Hypothesis (H 0 ): The population means of the two groups are equal. This suggests that there is no significant difference between the two group means. [ H 0 : μ 1 = μ 2 ]
- Two-tailed test: We are interested in any difference between the group means, but we don't specify a direction. [ H a : μ 1 ≠ μ 2 ]
- One-tailed test (upper-tailed): We are specifically interested in whether the mean of group 1 is greater than the mean of group 2. [ H a : μ 1 > μ 2 ]
- One-tailed test (lower-tailed): We are specifically interested in whether the mean of group 1 is less than the mean of group 2. [ H a : μ 1 2 ]
When conducting an independent t-test, you'd choose the form of the alternative hypothesis based on your research question or specific hypothesis. After performing the test, if the test statistic (t-value) is found to be in the critical region (typically using a significance level like 0.05), you'd reject the null hypothesis in favor of the alternative hypothesis. If the t-value is not in the critical region, you'd fail to reject the null hypothesis, indicating that you didn't find enough evidence to suggest a significant difference between the two group means. How to calulate an independent t-test- Formulate the null hypothesis (H0) and the alternative hypothesis (H1). The null hypothesis typically assumes that there is no significant difference between the means of the two groups, while the alternative hypothesis assumes that there is a significant difference.
- Collect data from the two groups being compared, ensuring that the samples are independent and representative of the populations being studied.
- Calculate the sample means (x̄1 and x̄2), the sample standard deviations (s1 and s2), and the sample sizes (n1 and n2) for each group.
- Compute the t-value using the formula: t = (x̄1 - x̄2) / sqrt((s1^2/n1) + (s2^2/n2))
- Determine the degrees of freedom for the t-distribution, which is calculated using the formula: df = n1 + n2 - 2
- Compare the calculated t-value to the critical value from the t-distribution table (or use statistical software) at the desired level of significance (α).
- If the calculated t-value exceeds the critical value (i.e., it falls within the rejection region), then the null hypothesis is rejected, indicating that there is a significant difference between the means. If the calculated t-value does not exceed the critical value (i.e., it falls within the non-rejection region), then the null hypothesis is not rejected, suggesting that there is no significant difference between the means.
The p-value is important to reported in a independent samples t-tests, representing the probability of obtaining a difference as extreme as the observed one, assuming the null hypothesis is true. If the p-value is below the chosen significance level (α), typically 0.05, then the null hypothesis is rejected. Calculate Independent t-test onlineTherefore, to calculate an independent t-test online, you only need two independent samples. The samples should be normally distributed. Then simply copy the data into the table above, making sure that the first row of variables contains the name! To calculate a paired samples t-test , simply select two metric variables. Assumptions for Independent Samples T-testIndependence: The observations in each group are independent of each other. This means that the values in one group are not influenced by or related to the values in the other group. Normally Distributed Data: The data in each group should be approximately normally distributed. If the sample size is large enough (typically >30 observations in each group), the t-test can be robust to moderate deviations from normality. However, for smaller sample sizes, normality assumption becomes more critical. Homogeneity of Variance: The variances of the two groups should be approximately equal. This assumption is known as homoscedasticity. Unequal variances between groups can affect the accuracy of the t-test. Calculate the Effect Size for the Independent t-TestThe effect size for an independent t-test is a measure of the magnitude or strength of the difference between the means of two independent groups. It provides information about the practical significance of the observed difference, which can be valuable in addition to the statistical significance determined by the t-test. There are several common effect size measures for independent t-tests, and two of the most widely used ones are Cohen's d and Hedges' g. Cohen's d is a standardized measure of effect size that expresses the difference between the means in terms of standard deviation units. The formula for Cohen's d is as follows: Cohen's d = (M1 - M2) / S_pooled - M1 is the mean of Group 1.
- M2 is the mean of Group 2.
- S_pooled is the pooled standard deviation, calculated as:
S_pooled = √((s1^2 + s2^2) / 2) Where s1 and s2 are the standard deviations of Group 1 and Group 2, respectively. Hedges' g is similar to Cohen's d but includes a correction factor for small sample sizes. It's useful when you have unequal group sizes or small sample sizes. The formula for Hedges' g is as follows: Hedges' g = (M1 - M2) / S_pooled * (1 - (3 / (4 * (N1 + N2) - 9))) - S_pooled is the pooled standard deviation, calculated as described above.
- N1 is the sample size of Group 1.
- N2 is the sample size of Group 2.
Once you have calculated Cohen's d or Hedges' g, you can interpret the effect size using general guidelines. Cohen's original guidelines suggest that: - Small effect size: d ≈ 0.2
- Medium effect size: d ≈ 0.5
- Large effect size: d ≈ 0.8
However, it's important to note that the interpretation of effect size can be context-dependent and may vary by field or research area. In some cases, even a small effect size can be practically significant, while in others, a large effect size may not have much practical relevance. Therefore, it's essential to consider the specific context of your study when interpreting the effect size. Dive Deep into Data with the Independent t-test CalculatorThe statistical realm can seem intimidating, with its barrage of numbers and terms. But when armed with the right tools, it becomes a fascinating world to explore. Introducing the independent t-test calculator - a beacon for those navigating the seas of independent data sets! Decoding the Independent t-testBefore we delve into the intricacies of the calculator, let's decode the basics. The independent t-test, often referred to as the two-sample t-test, determines whether there's a significant difference between the means of two unrelated groups. For instance, comparing the exam scores of students from two separate classes is a fitting application of this test. Why Choose the Independent t-test Calculator?- Efficiency : Bypass time-consuming manual calculations and swiftly gain insights.
- Accuracy : Harness the power of precise algorithms to ensure error-free results.
- User-friendly : Designed with simplicity in mind, the tool is accessible for novices and pros alike.
How to Use Our Calculator Efficiently- Enter Data : Populate the given fields with the data sets for both groups.
- Select Significance Level : Commonly set at 0.05, but can be tweaked based on your research needs.
- Compute : Hit 'Calculate' and witness the tool's prowess.
Deciphering the OutputPost-calculation, you'll be greeted with a t-value and a p-value. - t-value : Signifies the size of the difference relative to the variance within the samples.
- p-value : Denotes the likelihood of observing your specific results (or more extreme) under the assumption that the null hypothesis is true.
A p-value smaller than your chosen significance level means you can reject the null hypothesis, pointing towards a significant difference between the two groups. Final ThoughtsThe independent t-test calculator stands as an indispensable ally for all venturing into the comparison of unrelated groups. For students, researchers, and data enthusiasts, this tool demystifies complex calculations, leading to enlightened data-driven decisions. Embrace the convenience and clarity of the independent t-test calculator and elevate your analytical journey!  t-Test CalculatorT-test - work with steps. Input Data : Data set x = 3, 11, 17, 28, 34 Data set y = 5, 8, 13, 19, 28 Total number of elements = 5 Objective : Find the t-score by using mean and standard deviation. Solution : Mean 1 = (3 + 11 + 17 + 28 + 34)/5 = 93/5 Mean 1 = 18.6 Mean 2 = (5 + 8 + 13 + 19 + 28)/5 = 73/5 Mean 2 = 14.6 SD1 = √(1/5 - 1) x ((3 - 18.6) 2 + ( 11 - 18.6) 2 + ( 17 - 18.6) 2 + ( 28 - 18.6) 2 + ( 34 - 18.6) 2 ) = √(1/4) x ((-15.6) 2 + (-7.6) 2 + (-1.6) 2 + (9.4) 2 + (15.4) 2 ) = √(0.25) x ((243.36) + (57.76) + (2.56) + (88.36) + (237.16)) = √(0.25) x 629.2 = √157.3 SD1 = 12.5419 SD2 = √(1/5 - 1) x ((5 - 14.6) 2 + ( 8 - 14.6) 2 + ( 13 - 14.6) 2 + ( 19 - 14.6) 2 + ( 28 - 14.6) 2 ) = √(1/4) x ((-9.6) 2 + (-6.6) 2 + (-1.6) 2 + (4.4) 2 + (13.4) 2 ) = √(0.25) x ((92.16) + (43.56) + (2.56) + (19.36) + (179.56)) = √(0.25) x 337.2 = √84.3 SD2 = 9.1815 t-score = x 1 - x 2 √(SD1 2 /n1 + SD2 2 /n2) = 18.6 - 14.6 √((12.5419) 2 /5 + (9.1815) 2 /5) = 4 √((157.3)/5 + (84.3)/5) = 4 √(31.46 + 16.86) = 4 √(48.32) = 4 6.9513 t-score = 0.5754 What is t-Test?A hypothesis test consists of two hypotheses, the null hypothesis and the alternative hypothesis or research hypothesis. The symbol $H_0$ represents the null hypothesis. The null hypothesis reflects that there will be no observed effect on the experiment. The null hypothesis consists of an equal sign. The alternative hypothesis reflects that there is an observed effect on the experiment. The symbol $H_a$ represents the alternative hypothesis. The first step in testing is to determine the null hypothesis and the alternative hypothesis. Regarding the testing hypothesis, there are some important terms. Rejection region is the set of values leads to rejection of the null hypothesis. Non-rejection region is the set of values that leads to nonrejection of the null hypothesis. Critical values are the value that separates the rejection and non-rejection regions. The t-Test is used in comparing the means of two populations. There are two approaches: How to Find t-Critical ValueT-test with mean and standard deviation. A t-Test is one of the most frequently used tests in statistics. A t-Test is useful to conclude if the results are correct and applicable to the entire population. If we want to analyze simple experiments or when making simple comparisons between levels of independent variable we use the t-Test. It's used in comparison between two separate groups of individuals, for example: male vs female, experimental vs control group, etc. Practice Problem 1: There are two company A and B. We want to test average age of employees at these companies so we use a random sample of employee ages from each company. | Company A | Company B | | Mean | 43.2 | 36.7 | | Standard Deviation | 7 | 8.3 | | Number of Employess | 50 | 66 |
| Serbia | United States | | Mean | 43.2 | 5.2 | | Standard Deviation | 1.2 | 8.3 | | Number of Employess | 67 | 166 |
 Hypothesis Testing CalculatorUnderstanding Hypothesis Testing: A Guide to the Hypothesis Testing Calculator Hypothesis testing is a crucial statistical method used to make informed decisions about data and draw conclusions. Whether you’re a student, researcher, or professional, a Hypothesis Testing Calculator can be an invaluable tool in your statistical toolkit. Let’s explore what hypothesis testing is and how this calculator can assist you: Hypothesis Testing Basics: - Null Hypothesis (H0): This is the default assumption or claim that there is no significant difference or effect. It’s often denoted as H0.
- Alternative Hypothesis (Ha): This is the statement that contradicts the null hypothesis. It suggests that there is a significant difference or effect. It’s denoted as Ha.
- Significance Level (α): This is the predetermined threshold (e.g., 0.05 or 5%) used to determine statistical significance. If the calculated p-value is less than α, you reject the null hypothesis.
- p-value: This is the probability of observing the results (or more extreme results) if the null hypothesis is true. A small p-value suggests that the results are unlikely under the null hypothesis.
Key Features of the Hypothesis Testing Calculator: - Input Parameters: The calculator typically requires you to input sample data, choose the type of test (e.g., t-test, chi-square test), specify the null and alternative hypotheses, and set the significance level.
- Calculations: Once you input the data and parameters, the calculator performs the necessary statistical tests and calculations. It generates results such as the test statistic, degrees of freedom, and the p-value.
- Interpretation: Based on the results, the calculator helps you determine whether to reject or fail to reject the null hypothesis. It provides an interpretation of the findings, which is crucial for drawing conclusions.
- Visual Representation: Some calculators may offer visual aids like graphs or charts to help you better understand the data distribution and test results.
Significance of the Hypothesis Testing Calculator: - Scientific Research: Researchers across various fields use hypothesis testing to validate their hypotheses and draw meaningful conclusions from data.
- Quality Control: Industries use hypothesis testing to ensure the quality and consistency of products and processes.
- Medical Studies: In medical research, hypothesis testing helps assess the effectiveness of treatments or interventions.
- Academics: Students and educators use hypothesis testing to teach and learn statistical concepts and conduct experiments.
- Data-Driven Decisions: Businesses use hypothesis testing to make data-driven decisions, such as whether to launch a new product based on market research.
Conclusion: The Hypothesis Testing Calculator is a powerful tool that simplifies complex statistical analysis and enables data-driven decision-making. Whether you’re conducting experiments, analyzing survey data, or performing quality control, understanding hypothesis testing and using this calculator can help you make informed choices and contribute to evidence-based research and decision-making.  Informative Conversion Calculator  Follow Us On: Test Statistic Calculator Choose the method, enter the values into the test statistic calculator, and click on the “Calculate” button to calculate the statistical value for hypothesis evaluation. Add this calculator to your site This test statistic calculator helps to find the static value for hypothesis testing. The calculated test value shows if there’s enough evidence to reject a null hypothesis. Also, this calculator performs calculations of either for one population mean, comparing two means, single population proportion, and two population proportions. Our tool is highly useful in various fields like research, experimentation, quality control, and data analysis. What is Test Statistics?A test statistic is a numerical value obtained from the sample data set. It summarizes the differences between what you observe within your sample and what would be expected if a hypothesis were true. The t-test statistic also shows how closely your data matches the predicted distribution among the sample tests you perform. How to Calculate Test Statistics Value?- Collect the data from the populations
- Use the data to find the standard deviation of the population
- Calculate the mean (μ) of the population using this data
- Determine the z-value or sample size
- Use the suitable test statistic formula and get the results
Test Statistic For One Population Mean:Test statistics for a single population mean is calculated when a variable is numeric and involves one population or a group. x̄ - µ 0 σ / √n - x̄ = Mean of your sample data
- µ 0 = Hypothesized population mean that you are comparing to your sample mean
- σ = Population standard deviation
- n = number of observations (sample size) in your data set
Suppose we want to test if the average height of adult males in a city is 70 inches. We take a sample of 25 adult males and find the sample mean height to be 71 inches with a sample standard deviation of 3 inches. We use a significance level of 0.05. t = 70 - 71 3√25 Test Statistic Comparing Two Population Means:This test is applied when the numeric value is compared across the various populations or groups. To compute the resulting t statistic, two distinct random samples must be chosen, one from each population. \(\frac{√x̄ - √ȳ}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\) - ȳ = means of hypothesized population
Suppose we want to test if there is a difference in average test scores between two schools. We take a sample of 30 students from school A with an average score of 85 and a standard deviation of 5, and a sample of 35 students from school B with an average score of 82 and a standard deviation of 6. t = 85 - 82 √5 2 / 30 + 6 2 / 35 t = 3 √ 25/30 + 36/35 t = 3 √0.833 + 1.029 t = 3 √1.862 Test Statistic For a Single Population Proportion:This test is used to determine if a single population's proportion differs from a specified standard. The t statistic calculator works for a population proportion when dealing with data by having a limit of P₀ because proportions represent parts of a whole and cannot logically exceed the total or be negative. \(\frac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\) - P̂ = Sample proportion
- P 0 = Population proportion
Suppose we want to test if the proportion of left-handed people in a population is 10%. We take a sample of 100 people and find that 8 are left-handed. We use a significance level of 0.05. = P̂ - P₀ √0.10 (1 - 0.10)/100 = 0.08 - 0.10 √0.10 (1 - 0.10)/100 = -0.02 √0.10 (0.9)/100 = -0.02 √0.009 = -0.02 0.03 = −0.67 Test Statistic For Two Population Proportion:This test identifies the difference in proportions between two independent groups to assess their significance. \(\frac{\hat{p}_{1}-\hat{p}_{2}}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{n_{1}}+\frac{1}{n_{2}})}}\) - P̂ 1 and P̂ 2 = Sample proportions for two groups
Suppose we want to test if the proportion of smokers is different between two cities. We take a sample of 150 people from City A and find that 30 are smokers, and a sample of 200 people from City B and find that 50 are smokers. - P̂ 1 = 30 / 150 = 0.20
- P̂ 2 = 50 / 200 = 0.25
- P̂ = 30 + 50 / 150 + 200 = 0.229
Calculation: = 0.20 - 0.25 √0.229 (1 - 0.229) (1 / 150 + 1/200) = -0.05 √0.229 (0.771) (1 / 150 + 1 / 200) = -0.05 √0.176 (1/150 + 1/200) = -0.05 √0.176 (0.0113) = -0.05 √0.002 = -0.05 0.045 = −1.11 Sample Distribution Calculator Sample Size Calculator Effect Size Calculator Chi-Square Calculator Critical Value Calculator Probability Calculator Pie Chart Calculator Add this calculator to your site. Just copy a given code & paste it right now into your website HTML (source) for suitable page.  Give Us Your Feedback  Share Result  Get the ease of calculating anything from the source of calculator online Email us at © Copyrights 2024 by Calculator-Online.net One Sample T Test Calculator| | | | | Enter sample data Reporting results in APA styleOne sample t-test, what is a one sample t-test, how to use the one sample t test calculator, calculators.  - Calculators
- Descriptive Statistics
- Merchandise
- Which Statistics Test?
T-Test Calculator for 2 Independent MeansThis simple t -test calculator, provides full details of the t-test calculation, including sample mean, sum of squares and standard deviation. Further Information A t -test is used when you're looking at a numerical variable - for example, height - and then comparing the averages of two separate populations or groups (e.g., males and females). Requirements - Two independent samples
- Data should be normally distributed
- The two samples should have the same variance
Null Hypothesis H0: u1 - u2 = 0, where u1 is the mean of first population and u2 the mean of the second. As above, the null hypothesis tends to be that there is no difference between the means of the two populations; or, more formally, that the difference is zero (so, for example, that there is no difference between the average heights of two populations of males and females).  Z-test CalculatorTable of contents This Z-test calculator is a tool that helps you perform a one-sample Z-test on the population's mean . Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. You can also choose whether the calculator should determine the p-value from Z-test or you'd rather use the critical value approach! Read on to learn more about Z-test in statistics, and, in particular, when to use Z-tests, what is the Z-test formula, and whether to use Z-test vs. t-test. As a bonus, we give some step-by-step examples of how to perform Z-tests! Or you may also check our t-statistic calculator , where you can learn the concept of another essential statistic. If you are also interested in F-test, check our F-statistic calculator . What is a Z-test?A one sample Z-test is one of the most popular location tests. The null hypothesis is that the population mean value is equal to a given number, μ 0 \mu_0 μ 0 : We perform a two-tailed Z-test if we want to test whether the population mean is not μ 0 \mu_0 μ 0 : and a one-tailed Z-test if we want to test whether the population mean is less/greater than μ 0 \mu_0 μ 0 : Let us now discuss the assumptions of a one-sample Z-test. When do I use Z-tests?You may use a Z-test if your sample consists of independent data points and: the data is normally distributed , and you know the population variance ; the sample is large , and data follows a distribution which has a finite mean and variance. You don't need to know the population variance. The reason these two possibilities exist is that we want the test statistics that follow the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . In the former case, it is an exact standard normal distribution, while in the latter, it is approximately so, thanks to the central limit theorem. The question remains, "When is my sample considered large?" Well, there's no universal criterion. In general, the more data points you have, the better the approximation works. Statistics textbooks recommend having no fewer than 50 data points, while 30 is considered the bare minimum.  Z-test formulaLet x 1 , . . . , x n x_1, ..., x_n x 1 , ... , x n be an independent sample following the normal distribution N ( μ , σ 2 ) \mathrm N(\mu, \sigma^2) N ( μ , σ 2 ) , i.e., with a mean equal to μ \mu μ , and variance equal to σ 2 \sigma ^2 σ 2 . We pose the null hypothesis, H 0 : μ = μ 0 \mathrm H_0 \!\!:\!\! \mu = \mu_0 H 0 : μ = μ 0 . We define the test statistic, Z , as: x ˉ \bar x x ˉ is the sample mean, i.e., x ˉ = ( x 1 + . . . + x n ) / n \bar x = (x_1 + ... + x_n) / n x ˉ = ( x 1 + ... + x n ) / n ; μ 0 \mu_0 μ 0 is the mean postulated in H 0 \mathrm H_0 H 0 ; n n n is sample size; and σ \sigma σ is the population standard deviation. In what follows, the uppercase Z Z Z stands for the test statistic (treated as a random variable), while the lowercase z z z will denote an actual value of Z Z Z , computed for a given sample drawn from N(μ,σ²). If H 0 \mathrm H_0 H 0 holds, then the sum S n = x 1 + . . . + x n S_n = x_1 + ... + x_n S n = x 1 + ... + x n follows the normal distribution, with mean n μ 0 n \mu_0 n μ 0 and variance n 2 σ n^2 \sigma n 2 σ . As Z Z Z is the standardization (z-score) of S n / n S_n/n S n / n , we can conclude that the test statistic Z Z Z follows the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , provided that H 0 \mathrm H_0 H 0 is true. By the way, we have the z-score calculator if you want to focus on this value alone. If our data does not follow a normal distribution, or if the population standard deviation is unknown (and thus in the formula for Z Z Z we substitute the population standard deviation σ \sigma σ with sample standard deviation), then the test statistics Z Z Z is not necessarily normal. However, if the sample is sufficiently large, then the central limit theorem guarantees that Z Z Z is approximately N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . In the sections below, we will explain to you how to use the value of the test statistic, z z z , to make a decision , whether or not you should reject the null hypothesis . Two approaches can be used in order to arrive at that decision: the p-value approach, and critical value approach - and we cover both of them! Which one should you use? In the past, the critical value approach was more popular because it was difficult to calculate p-value from Z-test. However, with help of modern computers, we can do it fairly easily, and with decent precision. In general, you are strongly advised to report the p-value of your tests! p-value from Z-testFormally, the p-value is the smallest level of significance at which the null hypothesis could be rejected. More intuitively, p-value answers the questions: provided that I live in a world where the null hypothesis holds, how probable is it that the value of the test statistic will be at least as extreme as the z z z - value I've got for my sample? Hence, a small p-value means that your result is very improbable under the null hypothesis, and so there is strong evidence against the null hypothesis - the smaller the p-value, the stronger the evidence. To find the p-value, you have to calculate the probability that the test statistic, Z Z Z , is at least as extreme as the value we've actually observed, z z z , provided that the null hypothesis is true. (The probability of an event calculated under the assumption that H 0 \mathrm H_0 H 0 is true will be denoted as P r ( event ∣ H 0 ) \small \mathrm{Pr}(\text{event} | \mathrm{H_0}) Pr ( event ∣ H 0 ) .) It is the alternative hypothesis which determines what more extreme means : - Two-tailed Z-test: extreme values are those whose absolute value exceeds ∣ z ∣ |z| ∣ z ∣ , so those smaller than − ∣ z ∣ -|z| − ∣ z ∣ or greater than ∣ z ∣ |z| ∣ z ∣ . Therefore, we have:
The symmetry of the normal distribution gives: - Left-tailed Z-test: extreme values are those smaller than z z z , so
- Right-tailed Z-test: extreme values are those greater than z z z , so
To compute these probabilities, we can use the cumulative distribution function, (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , which for a real number, x x x , is defined as: Also, p-values can be nicely depicted as the area under the probability density function (pdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , due to: Two-tailed Z-test and one-tailed Z-testWith all the knowledge you've got from the previous section, you're ready to learn about Z-tests. From the fact that Φ ( − z ) = 1 − Φ ( z ) \Phi(-z) = 1 - \Phi(z) Φ ( − z ) = 1 − Φ ( z ) , we deduce that The p-value is the area under the probability distribution function (pdf) both to the left of − ∣ z ∣ -|z| − ∣ z ∣ , and to the right of ∣ z ∣ |z| ∣ z ∣ : 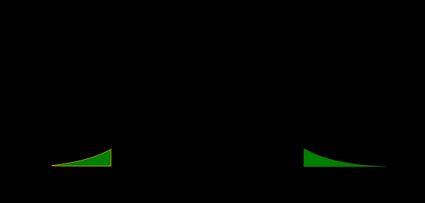 The p-value is the area under the pdf to the left of our z z z : 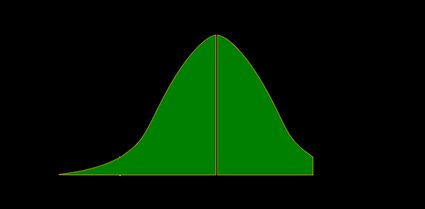 The p-value is the area under the pdf to the right of z z z :  The decision as to whether or not you should reject the null hypothesis can be now made at any significance level, α \alpha α , you desire! if the p-value is less than, or equal to, α \alpha α , the null hypothesis is rejected at this significance level; and if the p-value is greater than α \alpha α , then there is not enough evidence to reject the null hypothesis at this significance level. Z-test critical values & critical regionsThe critical value approach involves comparing the value of the test statistic obtained for our sample, z z z , to the so-called critical values . These values constitute the boundaries of regions where the test statistic is highly improbable to lie . Those regions are often referred to as the critical regions , or rejection regions . The decision of whether or not you should reject the null hypothesis is then based on whether or not our z z z belongs to the critical region. The critical regions depend on a significance level, α \alpha α , of the test, and on the alternative hypothesis. The choice of α \alpha α is arbitrary; in practice, the values of 0.1, 0.05, or 0.01 are most commonly used as α \alpha α . Once we agree on the value of α \alpha α , we can easily determine the critical regions of the Z-test: To decide the fate of H 0 \mathrm H_0 H 0 , check whether or not your z z z falls in the critical region: If yes, then reject H 0 \mathrm H_0 H 0 and accept H 1 \mathrm H_1 H 1 ; and If no, then there is not enough evidence to reject H 0 \mathrm H_0 H 0 . As you see, the formulae for the critical values of Z-tests involve the inverse, Φ − 1 \Phi^{-1} Φ − 1 , of the cumulative distribution function (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . How to use the one-sample Z-test calculator?Our calculator reduces all the complicated steps: Choose the alternative hypothesis: two-tailed or left/right-tailed. In our Z-test calculator, you can decide whether to use the p-value or critical regions approach. In the latter case, set the significance level, α \alpha α . Enter the value of the test statistic, z z z . If you don't know it, then you can enter some data that will allow us to calculate your z z z for you: - sample mean x ˉ \bar x x ˉ (If you have raw data, go to the average calculator to determine the mean);
- tested mean μ 0 \mu_0 μ 0 ;
- sample size n n n ; and
- population standard deviation σ \sigma σ (or sample standard deviation if your sample is large).
Results appear immediately below the calculator. If you want to find z z z based on p-value , please remember that in the case of two-tailed tests there are two possible values of z z z : one positive and one negative, and they are opposite numbers. This Z-test calculator returns the positive value in such a case. In order to find the other possible value of z z z for a given p-value, just take the number opposite to the value of z z z displayed by the calculator. Z-test examplesTo make sure that you've fully understood the essence of Z-test, let's go through some examples: - A bottle filling machine follows a normal distribution. Its standard deviation, as declared by the manufacturer, is equal to 30 ml. A juice seller claims that the volume poured in each bottle is, on average, one liter, i.e., 1000 ml, but we suspect that in fact the average volume is smaller than that...
Formally, the hypotheses that we set are the following: H 0 : μ = 1000 ml \mathrm H_0 \! : \mu = 1000 \text{ ml} H 0 : μ = 1000 ml H 1 : μ < 1000 ml \mathrm H_1 \! : \mu \lt 1000 \text{ ml} H 1 : μ < 1000 ml We went to a shop and bought a sample of 9 bottles. After carefully measuring the volume of juice in each bottle, we've obtained the following sample (in milliliters): 1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 \small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980 1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 . Sample size: n = 9 n = 9 n = 9 ; Sample mean: x ˉ = 980 m l \bar x = 980 \ \mathrm{ml} x ˉ = 980 ml ; Population standard deviation: σ = 30 m l \sigma = 30 \ \mathrm{ml} σ = 30 ml ; And, therefore, p-value = Φ ( − 2 ) ≈ 0.0228 \text{p-value} = \Phi(-2) \approx 0.0228 p-value = Φ ( − 2 ) ≈ 0.0228 . As 0.0228 < 0.05 0.0228 \lt 0.05 0.0228 < 0.05 , we conclude that our suspicions aren't groundless; at the most common significance level, 0.05, we would reject the producer's claim, H 0 \mathrm H_0 H 0 , and accept the alternative hypothesis, H 1 \mathrm H_1 H 1 . We tossed a coin 50 times. We got 20 tails and 30 heads. Is there sufficient evidence to claim that the coin is biased? Clearly, our data follows Bernoulli distribution, with some success probability p p p and variance σ 2 = p ( 1 − p ) \sigma^2 = p (1-p) σ 2 = p ( 1 − p ) . However, the sample is large, so we can safely perform a Z-test. We adopt the convention that getting tails is a success. Let us state the null and alternative hypotheses: H 0 : p = 0.5 \mathrm H_0 \! : p = 0.5 H 0 : p = 0.5 (the coin is fair - the probability of tails is 0.5 0.5 0.5 ) H 1 : p ≠ 0.5 \mathrm H_1 \! : p \ne 0.5 H 1 : p = 0.5 (the coin is biased - the probability of tails differs from 0.5 0.5 0.5 ) In our sample we have 20 successes (denoted by ones) and 30 failures (denoted by zeros), so: Sample size n = 50 n = 50 n = 50 ; Sample mean x ˉ = 20 / 50 = 0.4 \bar x = 20/50 = 0.4 x ˉ = 20/50 = 0.4 ; Population standard deviation is given by σ = 0.5 × 0.5 \sigma = \sqrt{0.5 \times 0.5} σ = 0.5 × 0.5 (because 0.5 0.5 0.5 is the proportion p p p hypothesized in H 0 \mathrm H_0 H 0 ). Hence, σ = 0.5 \sigma = 0.5 σ = 0.5 ; Since 0.1573 > 0.1 0.1573 \gt 0.1 0.1573 > 0.1 we don't have enough evidence to reject the claim that the coin is fair , even at such a large significance level as 0.1 0.1 0.1 . In that case, you may safely toss it to your Witcher or use the coin flip probability calculator to find your chances of getting, e.g., 10 heads in a row (which are extremely low!). What is the difference between Z-test vs t-test?We use a t-test for testing the population mean of a normally distributed dataset which had an unknown population standard deviation . We get this by replacing the population standard deviation in the Z-test statistic formula by the sample standard deviation, which means that this new test statistic follows (provided that H₀ holds) the t-Student distribution with n-1 degrees of freedom instead of N(0,1) . When should I use t-test over the Z-test?For large samples, the t-Student distribution with n degrees of freedom approaches the N(0,1). Hence, as long as there are a sufficient number of data points (at least 30), it does not really matter whether you use the Z-test or the t-test, since the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test instead of Z-test . How do I calculate the Z test statistic?To calculate the Z test statistic: - Compute the arithmetic mean of your sample .
- From this mean subtract the mean postulated in null hypothesis .
- Multiply by the square root of size sample .
- Divide by the population standard deviation .
- That's it, you've just computed the Z test statistic!
Here, we perform a Z-test for population mean μ. Null hypothesis H₀: μ = μ₀. Alternative hypothesis H₁ Significance level α The probability that we reject the true hypothesis H₀ (type I error). - AI Math Solver Graphing Calculator Popular Problems Worksheets Study Guides Cheat Sheets Calculators Verify Solution
- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
- A P-value calculator is used to determine the statistical significance of an observed result in hypothesis testing. It takes as input the observed test statistic, the null hypothesis, and the relevant parameters of the statistical test (such as degrees of freedom), and computes the p-value. The p-value represents the probability of obtaining results as extreme as, or more extreme than, the observed data, assuming the null hypothesis is true. A lower p-value suggests stronger evidence against the null hypothesis, indicating that the observed result is unlikely to have occurred by random chance alone. The calculated p-value is used in comparison with a predefined significance level (alpha) to make decisions about the null hypothesis. If the p-value is less than or equal to alpha, typically 0.05, the results are considered statistically significant, leading to the rejection of the null hypothesis in favor of the alternative hypothesis. If the p-value is greater than alpha, there is insufficient evidence to reject the null hypothesis.
- How do I calculate p-value?
- The p-value is calculated by determining the probability of observing a test statistic as extreme as, or more extreme than, the observed one under the assumption of the null hypothesis.
- What is p-value in Z test?
- In a Z-test, the p-value is the probability of observing a Z-statistic as extreme as, or more extreme than, the calculated one, assuming a normal distribution and under the null hypothesis.
- What is the p-value?
- The p-value, or probability value, is a measure in statistics that quantifies the strength of evidence against a null hypothesis. It indicates the likelihood of observing a test statistic as extreme as, or more extreme than, the one obtained from the data, assuming the null hypothesis is true.
- What is the alpha for p-value?
- The alpha (α) for a p-value is the chosen level of significance that determines the threshold for rejecting the null hypothesis. It represents the maximum probability of making a Type I error (incorrectly rejecting a true null hypothesis) and is typically set at common values such as 0.05 or 0.01.
- What does p-value under 0.05 mean?
- A p-value under 0.05 typically suggests that there is statistically significant evidence to reject the null hypothesis in favor of an alternative hypothesis.
 We want your feedbackPlease add a message. Message received. Thanks for the feedback. Calculator: One-Sample t-Test One-Sample t-Test CalculatorThis calculator will conduct a complete one-sample t-test, given the sample mean, the sample size, the hypothesized mean, and the sample standard deviation. The results generated by the calculator include the t-statistic, the degrees of freedom, the critical t-values for both one-tailed (directional) and two-tailed (non-directional) hypotheses, and the one-tailed and two-tailed probability values associated with the test. Please enter the necessary parameter values, and then click 'Calculate'. | | | | | Sample mean (x): | | | | Sample size: | | | | Sample standard deviation: | | | An open portfolio of interoperable, industry leading products The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.  Statistical analysis and graphing software for scientists Bioinformatics, cloning, and antibody discovery software Plan, visualize, & document core molecular biology procedures Electronic Lab Notebook to organize, search and share data Proteomics software for analysis of mass spec data Modern cytometry analysis platform Analysis, statistics, graphing and reporting of flow cytometry data Software to optimize designs of clinical trials POPULAR USE CASES T test calculatorA t test compares the means of two groups. There are several types of two sample t tests and this calculator focuses on the three most common: unpaired, welch's, and paired t tests. Directions for using the calculator are listed below, along with more information about two sample t tests and help on which is appropriate for your analysis. NOTE: This is not the same as a one sample t test; for that, you need this One sample t test calculator . 1. Choose data entry formatCaution: Changing format will erase your data. 2. Choose a testHelp me choose 3. Enter dataHelp me arrange the data 4. View the resultsWhat is a t test. A t test is used to measure the difference between exactly two means. Its focus is on the same numeric data variable rather than counts or correlations between multiple variables. If you are taking the average of a sample of measurements, t tests are the most commonly used method to evaluate that data. It is particularly useful for small samples of less than 30 observations. For example, you might compare whether systolic blood pressure differs between a control and treated group, between men and women, or any other two groups. This calculator uses a two-sample t test, which compares two datasets to see if their means are statistically different. That is different from a one sample t test , which compares the mean of your sample to some proposed theoretical value. The most general formula for a t test is composed of two means (M1 and M2) and the overall standard error (SE) of the two samples: 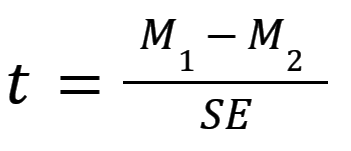 See our video on How to Perform a Two-sample t test for an intuitive explanation of t tests and an example. How to use the t test calculator- Choose your data entry format . This will change how section 3 on the page looks. The first two options are for entering your data points themselves, either manually or by copy & paste. The last two are for entering the means for each group, along with the number of observations (N) and either the standard error of that mean (SEM) or standard deviation of the dataset (SD) standard error. If you have already calculated these summary statistics, the latter options will save you time.
- Choose a test from the three options: Unpaired t test, Welch's unpaired t test, or Paired t test. Use our Ultimate Guide to t tests if you are unsure which is appropriate, as it includes a section on "How do I know which t test to use?". Notice not all options are available if you enter means only.
- Enter data for the test, based on the format you chose in Step 1.
- Click Calculate Now and View the results. All options will perform a two-tailed test .
Performing t tests? We can help.Sign up for more information on how to perform t tests and other common statistical analyses. Common t test confusionIn addition to the number of t test options, t tests are often confused with completely different techniques as well. Here's how to keep them all straight. Correlation and regression are used to measure how much two factors move together. While t tests are part of regression analysis, they are focused on only one factor by comparing means in different samples. ANOVA is used for comparing means across three or more total groups. In contrast, t tests compare means between exactly two groups. Finally, contingency tables compare counts of observations within groups rather than a calculated average. Since t tests compare means of continuous variable between groups, contingency tables use methods such as chi square instead of t tests. Assumptions of t testsBecause there are several versions of t tests, it's important to check the assumptions to figure out which is best suited for your project. Here are our analysis checklists for unpaired t tests and paired t tests , which are the two most common. These (and the ultimate guide to t tests ) go into detail on the basic assumptions underlying any t test: - Exactly two groups
- Sample is normally distributed
- Independent observations
- Unequal or equal variance?
- Paired or unpaired data?
Interpreting resultsThe three different options for t tests have slightly different interpretations, but they all hinge on hypothesis testing and P values. You need to select a significance threshold for your P value (often 0.05) before doing the test. While P values can be easy to misinterpret , they are the most commonly used method to evaluate whether there is evidence of a difference between the sample of data collected and the null hypothesis. Once you have run the correct t test, look at the resulting P value. If the test result is less than your threshold, you have enough evidence to conclude that the data are significantly different. If the test result is larger or equal to your threshold, you cannot conclude that there is a difference. However, you cannot conclude that there was definitively no difference either. It's possible that a dataset with more observations would have resulted in a different conclusion. Depending on the test you run, you may see other statistics that were used to calculate the P value, including the mean difference, t statistic, degrees of freedom, and standard error. The confidence interval and a review of your dataset is given as well on the results page. Graphing t testsThis calculator does not provide a chart or graph of t tests, however, graphing is an important part of analysis because it can help explain the results of the t test and highlight any potential outliers. See our Prism guide for some graphing tips for both unpaired and paired t tests. Prism is built for customized, publication quality graphics and charts. For t tests we recommend simply plotting the datapoints themselves and the mean, or an estimation plot . Another popular approach is to use a violin plot, like those available in Prism. For more informationOur ultimate guide to t tests includes examples, links, and intuitive explanations on the subject. It is quite simply the best place to start if you're looking for more about t tests! If you enjoyed this calculator, you will love using Prism for analysis. Take a free 30-day trial to do more with your data, such as: - Clear guidance to pick the right t test and detailed results summaries
- Custom, publication quality t test graphics, violin plots, and more
- More t test options, including normality testing as well as nested and multiple t tests
- Non-parametric test alternatives such as Wilcoxon, Mann-Whitney, and Kolmogorov-Smirnov
Check out our video on how to perform a t test in Prism , for an example from start to finish! Remember, this page is just for two sample t tests. If you only have one sample, you need to use this calculator instead. We Recommend:Analyze, graph and present your scientific work easily with GraphPad Prism. No coding required. - All online calculators
- Suggest a calculator
- Translation
PLANETCALC Online calculatorsTwo sample t-TestThe calculator to perform t-Test for the Significance of the Difference between the Means of Two Independent Samples The calculator below implements the most known statistical test, namely, the Independent Samples t-test or Two samples t-test. t-test, also known as Student's t-test, after William Sealy Gosset. "Student" was his pen name. The test deals with the null hypothesis such that the means of two populations are equal. To put it in other words, the difference we find between the means of the two samples should not significantly differ from zero. Again, the test works only if certain assumptions are met. These are: - That the two samples are independently and randomly drawn from the source population(s).
- That the scale of measurement for both samples has the properties of an equal-interval scale.
- That the source population(s) can be reasonably supposed to have a normal distribution.
- And, for this particular implementation of the test, that the variance of each population is the same
The calculator displays a level of confidence for both directional and non-directional tests. Let's say you get the result of 96%. Essentially this means that you have 96% confidence that the obtained difference shows something more than simple luck. The chance that you can get the obtained difference and the means of the two samples are the same is only 4%. This is the level of significance you calculate. Now, depending on your chosen level of significance, you can reject or fail to reject your null hypothesis.  If you care to find more, you can read excellent explanations here , starting from Chapter 9.  Two samples t-TestSimilar calculators. - • Student t-distribution
- • PlanetCalc statistics
- • P-value
- • Estimated Mean of a Population
- • Binomial distribution, probability density function, cumulative distribution function, mean and variance
- • Statistics section ( 37 calculators )
Share this pageTeach yourself statistics Bartlett's Test CalculatorBartlett's test is used to test the assumption that variances are equal (homogeneous) across groups. For help in using this calculator, read the Frequently-Asked Questions or review the Sample Problem . To learn more about Bartlett's test, read Stat Trek's tutorial on Bartlett's test . - In the dropdown box, specify the number of groups.
- Enter a value in each of the unshaded textboxes.
- Click Calculate to compute outputs.
Frequently-Asked QuestionsInstructions: To find the answer to a frequently-asked question, simply click on the question. What is Bartlett's test?Bartlett's test is used to test the assumption that variances are equal (i.e., homogeneous) across groups. The test is easy to implement and produces valid results, assuming data points within groups are randomly sampled from a normal distribution. Because Bartlett's test is sensitive to departures from normality, a normality test is prudent. Several ways to check for departures from normality are described at: How to Test for Normality: Three Simple Tests . Note: Unlike Hartley's Fmax test , which also tests for homogeneity, Bartlett's test does not assume equal sample sizes across groups. How does Bartlett's test work?Bartlett's test is an actual hypothesis test , where we examine observed data to choose between two statistical hypotheses: H 0 : σ 2 i = σ 2 j for all groups H 0 : σ 2 i ≠ σ 2 j for at least one pair of groups Like many other techniques for testing hypotheses, Bartlett's test for homogeneity involves computing a test-statistic and finding the P-value for the test statistic, given degrees of freedom and significance level . If the P-value is bigger than the significance level, we accept the null hypothesis; if it is smaller, we reject the null hypothesis. What steps (computations) are required to execute Bartlett's test?The steps required to conduct Bartlett's test for homogeneity are detailed below: - Step 1. Specify the significance level ( α ).
s 2 j = [ Σ ( X i, j - X j ) 2 ] / ( n j - 1 ) where X i, j is the score for observation i in Group j , X j is the mean of Group j , n j is the number of observations in Group j , and k is the number of groups. N = Σ n i s 2 p = [ Σ ( n j -1 ) s 2 j ] / ( N - K ) where n j is the sample size in Group j , k is the number of groups, N is the total sample size, and s 2 j is the sample variance in Group j . A = ( N - k ) * ln( s 2 p ) B = Σ [ ( n j - 1 ) * ln( s 2 j ) ] C = 1 / [ 3 * ( k - 1 ) ] D = Σ [ 1 / ( n j - 1 ) - 1 / ( N - k ) ] T = ( A - B ) / [ 1 + ( C * D ) ] where A is the first term in the numerator of the test statistic, B is the second term in the numerator, C is the first term in the denominator , D is the second term in the denominator, and ln is the natural logarithm. It turns out that the test statistic (T) is distributed much like a chi-square statistic with ( k-1 ) degrees of freedom. Knowing the value of T and the degrees of freedom associated with T, we can use Stat Trek's Chi-Square Calculator to find the P-value - the probability of seeing a test statistic more extreme than T. - Step 7. Accept or reject the null hypothesis, based on P-value and significance level. If the P-value is bigger than the significance level, we accept the null hypothesis that variances are equal across groups. Otherwise, we reject the null hypothesis.
What should I enter in the field for number of groups?Bartlett's is designed to test the hypothesis of homogeneity among nonoverlapping sets of data. The number of groups is the number of data sets under consideration. What should I enter for significance level?The significance level is the probability of rejecting the null hypothesis when it is true. Researchers often choose 0.05 or 0.01 for a significance level. What should I enter for sample size?Sample size refers to the number of observations in a group. For each group, enter the number of observations in the space provided. Note: Unlike some other tests for homogeneity (e.g., Hartley's Fmax test ), Bartlett's test does not require equal sample sizes across groups. What should I enter for variance?In the fields provided, enter an estimate of sample variance for each group. To compute sample variance ( s 2 j ) for each group, use the following formula: where X i, j is the score for observation i in Group j , X j is the mean of Group j , and n j is the number of observations in Group j . What is degrees of freedom?Bartlett's test computes a test statistic (T) to test for normality. The degrees of freedom ( df ) for a chi-square test of that statistic is: where N is the total sample size across all groups, and k is the number of groups in the sample. What is the test statistic (T)?The test statistic (T) is the statistic used by Bartlett's test to make a decision about whether to accept or reject the null hypothesis of equal variances between groups. When T is very big, we reject the null hypothesis; when T is small, we accept the null hypothesis. The calculator computes a T statistic, based on user inputs. The formulas that the calculator uses to compute a T statistic are given at Bartlett's Test for Homogeneity of Variance . What is the P-value?If you assume that the null hypothesis of equal variance is true, the P-value is the probability of seeing a test statistic (T) that is more extreme (bigger) than the actual test statistic computed from sample data. How does the calculator test hypotheses?Like many other techniques for testing hypotheses, Bartlett's test for homogeneity of variance involves computing a test-statistic and finding the P-value for the test statistic, given degrees of freedom and significance level . If the P-value is bigger than the significance level, the calculator accepts the null hypothesis. Otherwise, it rejects the null hypothesis. Sample ProblemsThe table below shows sample data and variance for five groups. How would you test the assumption that variances are equal across groups? | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | | Sample Data | 1
2
3
4
5 | 1
3
5
7
9 | 1
4
7
10
13 | 1
5
9
13
17 | 1
6
11
16
21 | | Variance | | 2.5 | 10 | 22.5 | 40 | 62.5 | One option would be to use Stat Trek's Bartlett's Test Calculator . Simply, take the following steps: - Enter the number of groups (5).
- Enter the significance level. For this problem, we'll use 0.05.
- For each group, enter sample size. In this example, the sample size is 5 for each group.
- For each group, enter a sample estimate of group variance.
Then, click the Calculate button to produce the output shown below: From the calculator, we see that the test statistic (T) is 8.91505. Assuming equal variances in groups and given a significance level of 0.05, the probability of observing a test statistic (T) bigger than 8.91505 is given by the P-value. Since the P-value (0.06326) is bigger than the significance level (0.05), we cannot reject the null hypothesis of equal variances across groups. Note: To see the hand calculations required to solve this problem, go to Bartlett's Test for Homogeneity of Variance: Example 1 . Oops! Something went wrong.  |















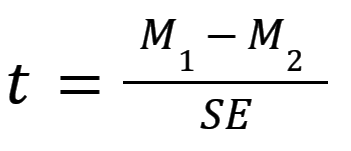
IMAGES
COMMENTS
Hypothesis Testing Calculator. The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is ...
Use this Hypothesis Test Calculator for quick results in Python and R. Learn the step-by-step hypothesis test process and why hypothesis testing is important. Learn . Courses Career Tracks Projects Upcoming Courses Certificates . Career Track Certificate ...
Alternative to statistical software like SPSS and STATA. DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no ...
This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing! Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and ...
Hypothesis testing is a foundational method used in statistics to infer the validity of a hypothesis about a population parameter. The Hypothesis Testing Calculator facilitates this process by automating the computations necessary for the t-test, a method used to compare sample means against a hypothesized mean or against each other.Let's delve into the formulas this calculator uses to ...
T-Test calculator. The Student's t-test is used to determine if means of two data sets differ significantly. This calculator will generate a step by step explanation on how to apply t - test. Two sample t-test One sample t-test.
Hypothesis Test Calculator. Upload your data set below to get started. Upload File. Or input your data as csv. column_one,column_two,column_three 1,2,3 4,5,6 7,8,9. Submit CSV. Sharing helps us build more free tools. Embed on Your Website.
Clear the table in the Hypothesis test calculator. Copy your data into the table. Select the variables. In the hypothesis test calculator you can calculate e.g. a t-test, a chi-square test, a binomial test or an analysis of variance. If you need a more detailed explanation, you can find more information in the tutorials.
To calculate a t-Test online just select one metric Variable and one nominal Variable with two values. Here you can easily calculate a t-test online, just copy your data into the upper table and select one or two variables. Paired t-test Calculator: If you click on two metric variables, a paired samples t test is calculated.
The p-value is important to reported in a independent samples t-tests, representing the probability of obtaining a difference as extreme as the observed one, assuming the null hypothesis is true. If the p-value is below the chosen significance level (α), typically 0.05, then the null hypothesis is rejected. Calculate Independent t-test online
Step 3: Click the "Perform Test" button. The tool will quickly process the information, performing the hypothesis test and generating a detailed report. Step 4: Review the results. The calculator provides the calculated t-value, critical value, and the test's conclusion. You can also visualize the sample distribution with a dynamic chart ...
t-test calculator is an online statistics tool to estimate the significance of observed differences between the means of two samples when there is a null hypothesis that is no significant difference between the means by using standard deviation. It is necessary to follow the next steps: Enter two samples (observed values) in the box. These values must be real numbers or variables and may be ...
Calculations: Once you input the data and parameters, the calculator performs the necessary statistical tests and calculations. It generates results such as the test statistic, degrees of freedom, and the p-value. Interpretation: Based on the results, the calculator helps you determine whether to reject or fail to reject the null hypothesis.
This test statistic calculator helps to find the static value for hypothesis testing. The calculated test value shows if there's enough evidence to reject a null hypothesis. Also, this calculator performs calculations of either for one population mean, comparing two means, single population proportion, and two population proportions.
Single Sample T-Test Calculator. A single sample t-test (or one sample t-test) is used to compare the mean of a single sample of scores to a known or hypothetical population mean. So, for example, it could be used to determine whether the mean diastolic blood pressure of a particular group differs from 85, a value determined by a previous study.
The one-sample t-test determines if the mean of a single sample is significantly different from a known population mean. The one sample t-test calculator calculates the one sample t-test p-value and the effect size. When you enter the raw data, the one sample t-test calculator provides also the Shapiro-Wilk normality test result and the outliers.
This simple t -test calculator, provides full details of the t-test calculation, including sample mean, sum of squares and standard deviation. A t -test is used when you're looking at a numerical variable - for example, height - and then comparing the averages of two separate populations or groups (e.g., males and females).
Choose the alternative hypothesis: two-tailed or left/right-tailed. In our Z-test calculator, you can decide whether to use the p-value or critical regions approach. In the latter case, set the significance level, α. \alpha α. Enter the value of the test statistic, z. z z.
A P-value calculator is used to determine the statistical significance of an observed result in hypothesis testing. It takes as input the observed test statistic, the null hypothesis, and the relevant parameters of the statistical test (such as degrees of freedom), and computes the p-value. The p-value represents the probability of obtaining ...
This calculator will conduct a complete one-sample t-test, given the sample mean, the sample size, the hypothesized mean, and the sample standard deviation. The results generated by the calculator include the t-statistic, the degrees of freedom, the critical t-values for both one-tailed (directional) and two-tailed (non-directional) hypotheses, and the one-tailed and two-tailed probability ...
A t test compares the means of two groups. There are several types of two sample t tests and this calculator focuses on the three most common: unpaired, welch's, and paired t tests. Directions for using the calculator are listed below, along with more information about two sample t tests and help on which is appropriate for your analysis. NOTE: This is not the same as a one sample t test; for ...
The calculator below implements the most known statistical test, namely, the Independent Samples t-test or Two samples t-test. t-test, also known as Student's t-test, after William Sealy Gosset. "Student" was his pen name. The test deals with the null hypothesis such that the means of two populations are equal.
Bartlett's test is an actual hypothesis test, where we examine observed data to choose between two statistical hypotheses: . Null hypothesis: Variance is equal across all groups. H 0: σ 2 i = σ 2 j for all groups. Alternative hypothesis: Variance is not equal across all groups. H 0: σ 2 i ≠ σ 2 j for at least one pair of groups